Графическая иллюстрация задачи нелинейного программирования

Пример 1

Пусть допустимая область определяется следующими ограничениями:

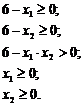
Графическая иллюстрация области допустимых решений приведена на рис. 18.1.

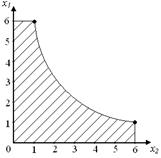
Рис. 18.1. Область допустимых решений

Пример 2

Допустимая область:

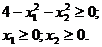
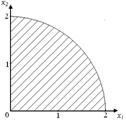
Рис. 18.2. Область допустимых решений

Пример 3

Найти максимум целевой функции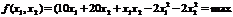

при ограничениях

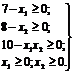
Графическая иллюстрация этой задачи показана на рис. 18.3.

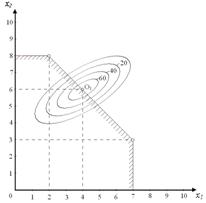
Рис. 18.3. Графическая иллюстрация задачи нелинейного программирования

Задаваясь значениями целевой функции 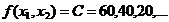, строится семейство эллипсов с общими осями (линии уровня целевой функции). Как видно из рис.18.3 точка О₁ с координатами х₁=4 и х₂=6 является решением задачи, т.к. в ней достигается максимум целевой функции на границе области допустимых решений.

Методы условной и безусловной оптимизации

(см. курс высшей математики)

В курсе высшей математики изучались методы безусловной оптимизации, когда ограничения на переменную отсутствуют (исследование максимума и минимума функции, т.е. исследование функции на экстремум).

В данной лекции мы будем изучать методы условной оптимизации, т.е. метод определения экстремума целевой функции при наличии ограничений.

4. Классический метод определения условного экстремума

Процесс решения состоит:

1.В определении внутри допустимого множества всех стационарных точек целевой функции 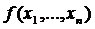, удовлетворяющих условию

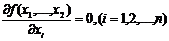
2.В проверке всех стационарных точек на максимум или минимум;

3.В сравнении этих значений с максимальными (минимальными) значениями, которых достигает целевая функция f на границе допустимого множества и выбор из них наиболее экстремальных.

Главный недостаток классического метода – отсутствие стандартизированной процедуры поиска оптимального решения, пригодной для любых видов ограничений.

Метод множителей Лагранжа

Используя этот метод можно отыскать максимум или минимум целевой функции при ограничении типа равенства. Основная идея метода заключается в переходе от задачи на условный экстремум (с ограничениями) к задаче отыскания экстремума специально построенной функции Лагранжа без ограничений. Рассмотрим следующую задачу

Найти

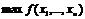(18.3)

при ограничениях

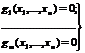(18.4)

причем функции f, g₁,…,g_m предполагают дифференцирование.

Вводится набор переменных 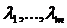(по числу ограничений), которые называются множителями Лагранжа, и составляется функция Лагранжа следующего вида

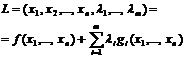(18.5)

Необходимыми условиями того, что точка 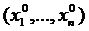представляет собой решение задачи (18.3) при ограничениях (18.4), будет выполнение следующих правил

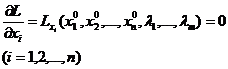(18.6)

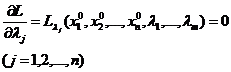(18.7)

Итак, метод множителей Лагранжа для задачи вида (18.3) с ограничениями (18.4) состоит из следующих этапов:

1. Составление функции Лагранжа (18.5);

2. Нахождение частных производных функции 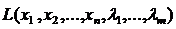по всем 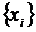и 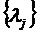и получение системы (18.6) из (n+m) уравнений с (n+m) переменными ;

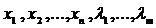Решение уравнений (18.6) и (18.7), нахождение точек 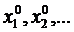, где имеются относительные экстремумы. Найденные точки исследуются на максимум и минимум