Главные оси и главные моменты инерции. Свойства главных осей и главных центральных осей инерции

Поскольку уравнение не содержит координат первой степени, то его центр совпадает с началом координат. Три оси симметрии эллипсоида инерции называются – главными осями инерции относительно точки 0, а момент инерции относительно осей – главным моментом инерции.

Если выбрать систему координат так, что бы оси совпадали с главными осями инерции механ. сист, то уравнение эллипса примет вид: J^*_x X²_* + J^*_y Y²_* + J^*_z Z²_* = 1

Каждой точке соотв. свой эллипс инерции и если он известен, то можно найти момент инерции относительно любой оси, проходящей через данную точку. Эллипсоид, соотв. центру масс тела называется центральным эллипсоидом инерции, а его оси симметрии главными центральными осями инерции.

Если известны главные центры моментов инерции, то можно построить центр эллипсоид. инерции, а отсюда следует определение: моментом инерции относительно любой оси, проходящей через центр масс системы

3. Две основные задачи динамики.

Первая задача динамики.

По заданному движению точки определить силу.

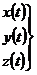- уравнения движения точки

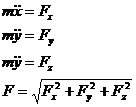
Решается методом дифференцирования.

Вторая задача динамики.

Решение второй задачи динамики составляет основное содержание всех разделов динамики.

По заданным силам определить движение точки. Задача решается методом интегрирования.

Если сила зависит только от t или только от x или V, то можно пользоваться следующими указаниями:

1) составить диф.уравнение движения точки:

а) начало координат совмещать с началом движения точки (или с её равновесным положением);

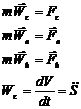
б) если движение по прямой, то одну из осей направить в сторону движения точки;

в) точку изобразить с приложенными силами в произвольном положении;

г) составить диф.уравнение в проекции на ось.

2) интегрирование диф.уравнения.

Замена переменных.

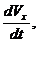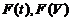
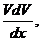если

если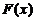

Диф.уравнение решать методом разделения переменных(кроме задач на колебания).

3) интегралы брать неопределёнными, учитывая постоянные интегрирования, найденные из начальных условий.

4) анализ движения точки.

Движение тел в воздухе при наличии сопротивления, пропорционального квадрату скорости.

При движении тел в газах в частности в воздухе при скорости до 300 м\с сила сопротивления пропорциональна квадрату скорости, т.е. где x- const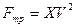

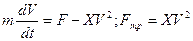
Дифференциальное уравнение относительного движения материальной точки.

1)Введем 2 вектора

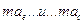
численно равные произведениям

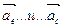и направленные противоположно ускорениям

Эти векторы назовём переносной и кориолисовой силами инерции.

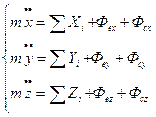
Дифф.ур-я относительного движения мат.точки.

Диф.уравнения движения материальной точки.

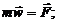
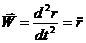
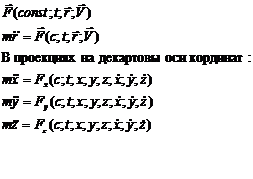
При плоском движении точки:

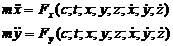
Если тело движется прямолинейно, то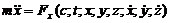

В проекциях на естественные оси координат:

, где S- закон движения точки по траектории.