Вопрос 1. Метод координат на прямой.

Вопрос 1. Метод координат на прямой.

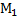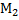На любой прямой можно выделить два направления положительное и отрицательное. Прямая на кот. стрелкой указанно положит. направление, назв. осью.Отрезок огранич. т. и назовем направленным отрезком(н.о.), если указано какая из т. 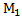и 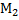явл. началом, а какая концом. Н.О.как и любой отрезок имеет длину,кот. обознач. 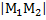. Н.О. расположен на оси имеет характерную величину. Велич. н.о.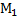 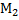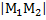некоторым оси дельта ( ) назовем его длину взятую со знаком +, если направление этого н.о. совпадет с положит. направлением оси дельта и со знаком – в противном случае. Велич. н.о.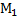 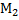обозначают 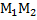. Длина н.о. = длине н.о. = = , = .

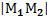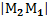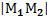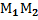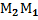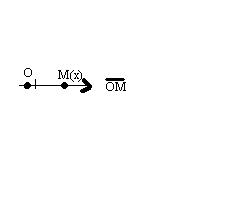РИС.3

Координатной прямой(к.п.) наз. ось на кот. зафиксировано начало отсчета и выбран маштаб и измерение длин.На рис.3 к.п. с началом отсчета О положит. направлением указаны стрелкой и еденицы маштаба. Координатой т. М к.п. наз. величину ОМ направленного отрезка ОМ. х=ОМ

Расстояние между точками ( 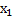), 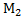( 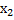) обозначают ρ ( 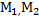)= 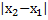.Величина по формуле: .

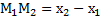Вопрос 2. Простое отношение 3-ех точек на оси.

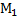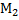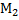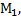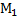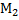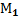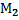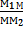Пусть , ,М три точки лежащие на одной оси,причем несоответствует ни с ни с М. Простым отнош. 3-ех точек , ,М взятых в указанном порядке наз. число λ=( , ,М)= .(1)

где 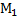М-величины,М 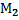-велич. направ.отрезка. Если т. М лежит внутри(вне) отрезка 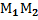,то говорят, что М делит отрезок 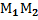внутренним(внешним) образом. При этом λ>0,(вне)

λ<0. Если λ=1,то М середина отрезка 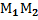.Пусть 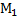( 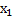), 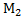( 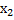),М(х) точки координатной прямой ОХ.Причем 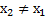, 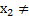х. Тогда по равенству 1,находим

λ=( 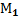, ,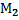М)= 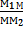= 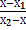,откуда

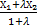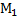
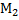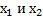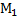х= .(2).формула (2) определяет координату т. М делящий направленный отрезок , в отношении λ, когда известны координаты т. и 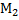. Если М(х)-сер. отрезка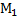 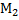, то (λ=1) и равенство (2) имеет вид: х= 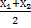.-среднее орифметич. координат.

Вопрос 3. Прямоугольные декартовы координаты на плоскости.

II I РИС.1

III IV

Прямоуг. декарт. система координат(ПДСК) на плоскости определяется заданием маштаба и двух перпендикулярных осей занумерованных в определенном порядке(Рис1). Ох-ось абсцисс,Оу-ось ординат. I,II,III,IV-четверти.

у 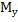М

Мх х

Прямоуг. декартовы т. М-это числа определенные равенствами:

х=ОМх,у=ОМу, где ОМх и ОМу величины направленных отрезков ОМх и ОМу, соответственно Ох,Оу. Запись М(х,у)означает, что т. М имеетабсциссу х и ординату у.Начало координатной О(о,о). Расстояние между двумя т. , .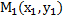

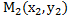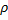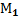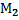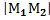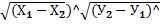( , )= = . (1)

Пусть даны т. 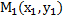, 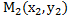координатной плоскости Оху, тогда координаты т. М(х,у) делящий направленный отрезок 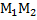, λ 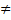– 1 определяется формулой:

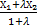х= , х= 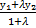. Если дани 3 точки не лежащие на одной прямой, то S∆ = ± [( )( )–( )( )]

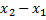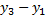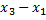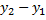Вопрос 7. Общее уравнение прямой.

Если на плоск. введена прямая система координат. Оху, то лин. ур-ние относительно ху 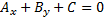, в кот. числа A и B одновременно не равны 0, т.е. 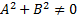, то это ур-ние определяет прямую. Частые виды ур-ние прямой получ. когда один или два коэф. равны 0, при выполняемыми условиями:

1)с=0 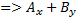=0(прямая проходит через начало координат)

2)А=0 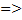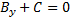(прямая параллельна оси Ох)

3)В=0 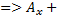С=0(прямая параллельна оси Оу)

4)А=0 и С=0 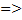у=0( прямая совпадает с осью Ох)

5)В=0,С=0 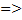х=0 (прямая совподает с осью Оу).

Вопрос 1. Метод координат на прямой.

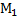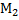На любой прямой можно выделить два направления положительное и отрицательное. Прямая на кот. стрелкой указанно положит. направление, назв. осью.Отрезок огранич. т. и назовем направленным отрезком(н.о.), если указано какая из т. 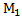и 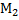явл. началом, а какая концом. Н.О.как и любой отрезок имеет длину,кот. обознач. 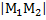. Н.О. расположен на оси имеет характерную величину. Велич. н.о.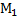 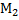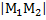некоторым оси дельта ( ) назовем его длину взятую со знаком +, если направление этого н.о. совпадет с положит. направлением оси дельта и со знаком – в противном случае. Велич. н.о.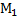 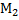обозначают 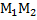. Длина н.о. = длине н.о. = = , = .

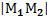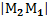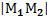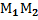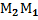РИС.3

Координатной прямой(к.п.) наз. ось на кот. зафиксировано начало отсчета и выбран маштаб и измерение длин.На рис.3 к.п. 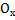с началом отсчета О положит. направлением указаны стрелкой и еденицы маштаба. Координатой т. М к.п. 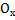наз. величину ОМ направленного отрезка ОМ. х=ОМ

Расстояние между точками 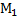( 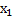), 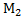( 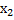) обозначают ρ ( 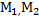)= 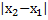.Величина по формуле: .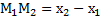