Тема: Решение логарифмических неравенств
Цели:
– научиться решать логарифмические неравенства;
– закрепить теоретические знания по теме: Логарифмическая функция.
Оснащение занятия: учебник, плакат, справочник.
Порядок выполнения работы:
Задание 1. Записать в конспект.
При решении неравенств вида следует помнить, что логарифмическая функция
возрастает при и убывает при (см. п. 18). Значит, в случае, когда, то от исходного неравенства нужно переходить к неравенству того же смысла. В случае же, когда, то от исходного неравенства следует переходить к неравенству противоположного смысла. При этом следует учитывать, что логарифмическая функция определена лишь на множестве положительных чисел.
В итоге от неравенства мы переходим к системе неравенств:
Задание 2. Разберите решение задач 1 и 2 (см. стр. 108) и составьте алгоритм решения логарифмических неравенств.
Задание 3. Выполните № 354 (1;3), № 355(1;3;5), № 357 по алгоритму.
Контроль знаний студентов:
Вариант-1. №356(1), № 381(3), № 382(2).
Вариант-2. №356(3), № 381(4), № 382(1).
Литература: Алимов Ш. А. Алгебра и начала анализа стр.98, стр.107.
Практическая работа № 23
Тема: Синус, косинус, тангенс и котангенс числа
Цели:
– научиться переводить градусную меру угла в радианную и, обратно, радианную меру угла в градусную;
– научиться определять знаки синуса, косинуса и тангенса в координатных четвертях;
– научиться применять формулы зависимости между тригонометрическими функциями одного и того же угла;
– изучить тему: «Синус, косинус и тангенс углов».
Оснащение занятия: учебник, конспекты, справочник.
Порядок выполнения работы
Задание 1. Вопросы для повторения.
1. Что называется, радианом?
2. Назовите формулу перевода градусной меры угла в радианную и, обратно, радианную меру угла в градусную.
3. Дайте определение синуса, косинуса и тангенса угла.
4. Какие знаки имеют синус, косинус и тангенс в координатных четвертях?
5. Какими соотношениями связаны тригонометрические функции одного и того же аргумента?
Задание 2. Выполните № 407 (неч.), № 408 (неч.), № 420 (неч.), № 423.
Задание 3. Разберите решение задачи 1 и 2 (стр.131) и выполните № 442 (неч.), № 447.
Задание 4. Используя формулы зависимости между тригонометрическими функциями одного и того же угла выполнить № 459(1;2;3;4).
Задание 5. Запишите в конспект формулы и примеры темы:
«Синус, косинус и тангенс углов» стр. 140 и выполните № 475 (неч.).
Литература: Алимов Ш. А. Алгебра и начала анализа с. 115, с.124, с.140, с.133.
Практическая работа №24
Тема: Основные тригонометрические тождества
Цели:
– научиться применять формулы сложения для преобразований выражений.
– научиться применять формулы синуса, косинуса и тангенса двойного угла для преобразований выражений.
Оснащение занятия: учебник, таблица значений синуса, косинуса, тангенса.
Порядок выполнения работы:
Задание 1. Познакомьтесь с содержанием п.28, стр.142 и запишите формулы сложения. Какие формулы называют формулами сложения?
Задание 2. а) Разберите задачи №1 и №2, стр.143 и запишите их в тетрадь.
б) Выполните (в парах) №481(2;4), №482(2;4), №483(2), №484(2;4).
Задание 3.а) Запишите в тетрадь задачи №4-№6, стр.144.
б) Выполните №485(четные)- №487(чет.)
Задание 4. а) Запишите формулу синуса двойного угла п.29, стр.147.
б) Разберите решение задачи №1.
в) Выполните №500(нечетные)-№503(неч).
Задание 5. а) Запишите формулу косинуса двойного угла.
б) Разберите решение задачи №2.
в) Выполните №500(четные)-№503(чет).
Задание 6. а) Запишите формулу тангенса двойного угла.
б) Разберите решение задачи №4.
в) Выполните №500(3)-№501(3), №505.
Задание 7. Организуйте работу парами и расскажите друг другу какие формулы вы сегодня применяли для преобразований тригонометрических выражений.
Литература: Алимов Ш. А. Алгебра и начала анализа стр.142, 147.
Практическая работа № 25
Тема: Преобразование графиков тригонометрических функций
Цели:
– научиться находить область определения и множество значений тригонометрических функций;
– научиться определять, является ли данная функция четной или нечетной;
– научиться строить график и с помощью графика описывать поведение функции при изменении аргумента;
– изучить свойства обратных тригонометрических функций.
Оснащение занятия: учебник, конспект, таблицы.
Порядок выполнения работы.
1. Вопросы для повторения.
– Какие функции называются тригонометрическими? Какова их область определения и множество значений?
– Какие тригонометрические функции являются четными, а какие нечетные?
– Что называется периодом функции? Какие периоды имеют тригонометрические функции?
2. Разберите решение задачи 1-3 стр.198 и выполните № 691(неч), № 692(неч).
3. Разберите решение задачи 1 стр.201 и выполните № 701(неч), №704(неч).
4. По рисунку 88, стр.205; по рисунку 91, стр.209; по рисунку 95, стр.214 назовите промежутки возрастания и убывания функций. Выполните №709 и №710, №721 и №722.
5. Как построить графики тригонометрических функций?
На странице 224 выполните задание 2 и 3.
6. Запишите в конспект ответы на вопросы:
– На каком промежутке изменений аргумента задается функция ?
– Дайте определение функции .
– Укажите область значений функции .
– Постройте график функции .
– Охарактеризуйте таким же образом функции .
Контроль знаний студентов:
– проверить практическую работу;
– индивидуальные вопросы по практической работе.
Литература: Ш. А. Алимов. Алгебра и начала анализа стр.204-218.
Практическая работа № 26
Тема: Формулы тригонометрии
Цели:
– научится использовать формулы приведения при выполнении преобразований тригонометрических выражений;
– научится применять формулы преобразования суммы (разности) синусов (косинусов) в произведение.
Оснащение занятия: учебник, конспект, таблица.
Порядок выполнения работы
Задание 1. Разберите задачу №1, стр.154 (§ 31) и запишите формулы (3)-(6).
Как называют формулы (5)-(6)?
Задание 2. Разберите решение задач №2 и №3, стр.155.
Задание 3. Запишите формулы (7)-(9). Как их называют?
Задание 4. Запишите правила, которые можно применить, чтобы записать любую формулу приведения (стр. 157).
Задание 5.
а) Выполните №525(1-4), №526(неч.), используя задачи №№2-4 как образец.
б) Выполните №527(1), №528(1).
Задание 6.
а) Разберите задачу №1, стр.159(параграф 32) и запишите формулы суммы и разности синусов (косинусов).
б) Разобрать задачи №2 и №3, стр.160.
Задание 7. Выполните №538-№539(неч.), №537(неч), №530–№531(неч.), №541(1).
Контроль знаний студентов:
– проверить практическую работу студентов;
– устный опрос.
1. Как называются формулы, которые вы сегодня применяли при выполнении упражнений?
2. Сформулируйте правила записи формул приведения.
3. Как формулы суммы (разности) синусов (косинусов) преобразовать в произведение?
Литература: Алимов Ш. А. Алгебра и начала анализа стр. 154, стр.159.
Практическая работа № 27
Тема: Преобразование суммы тригонометрическихвыражений в произведение
Цель: - Ввести формулы:
- суммы косинусов
cos  + cos
+ cos 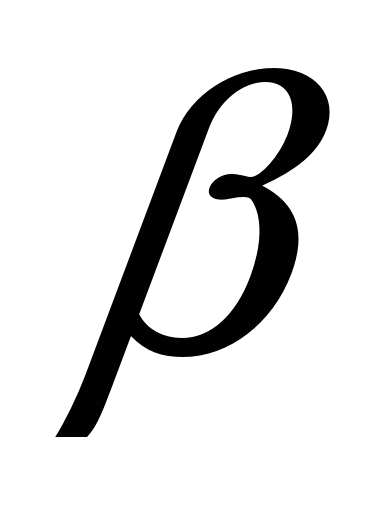 = 2 cos
= 2 cos  ×cos
×cos  ;
;
-разности синусов
cos  - cos
- cos 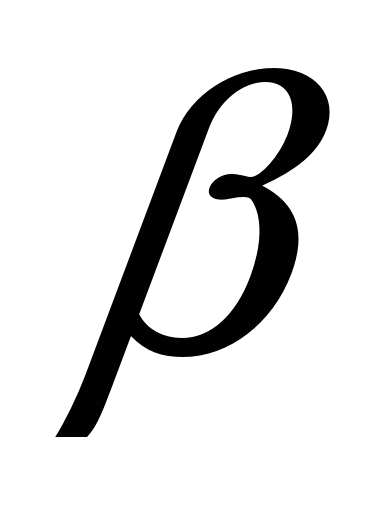 = -2 Sin
= -2 Sin 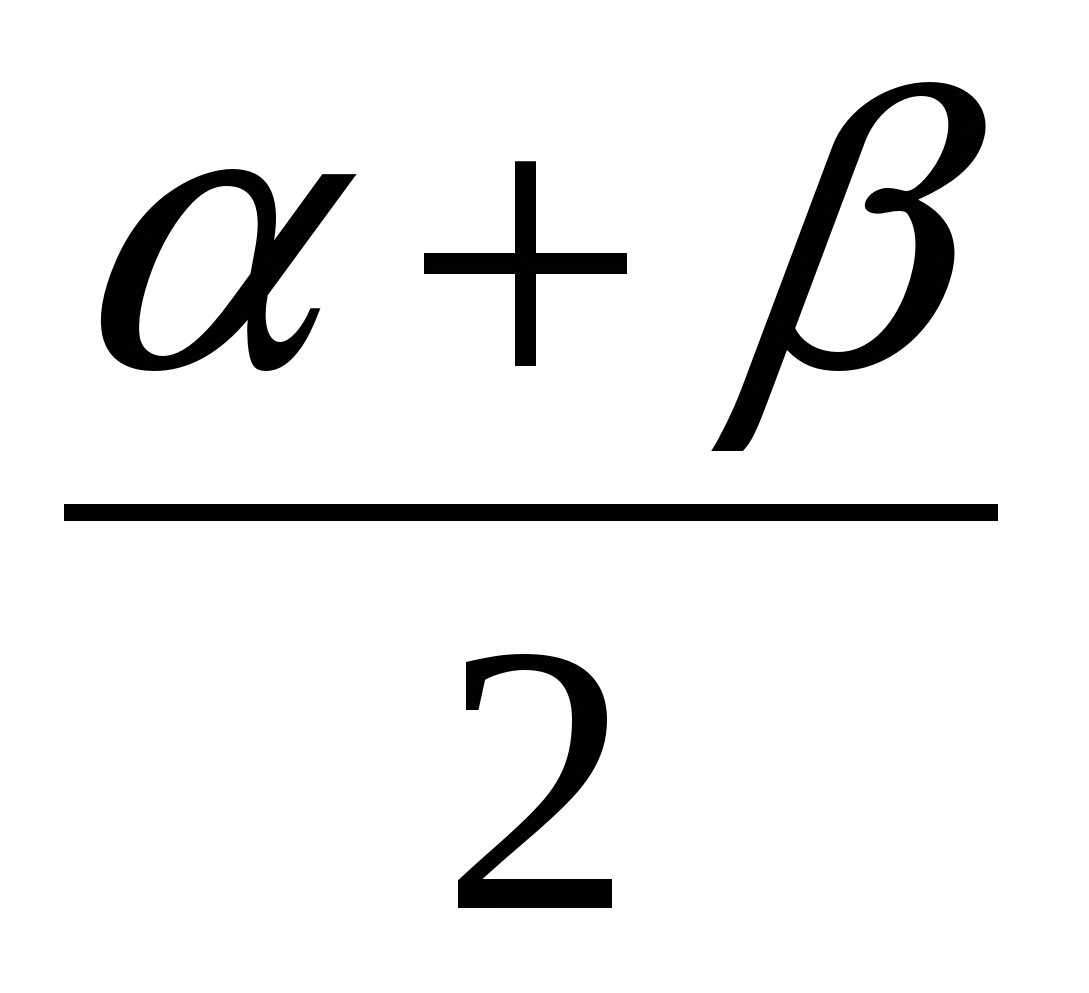 × Sin
× Sin 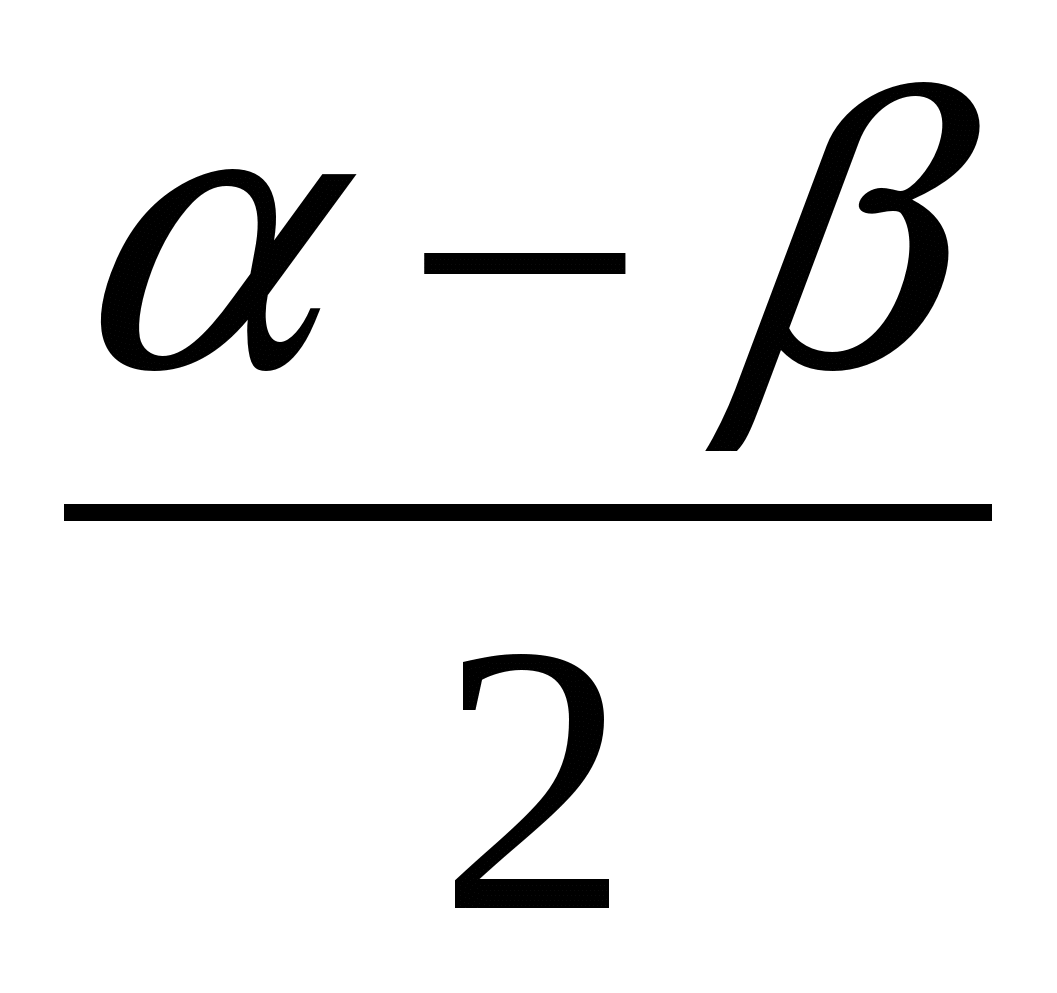 .
.
- Научить применять формулы суммы и разностикосинусов при выполнении упражнений.
Методическое обоснование
Пример 1.
Вычислить:
cos 1050 + cos750 = 2 cos 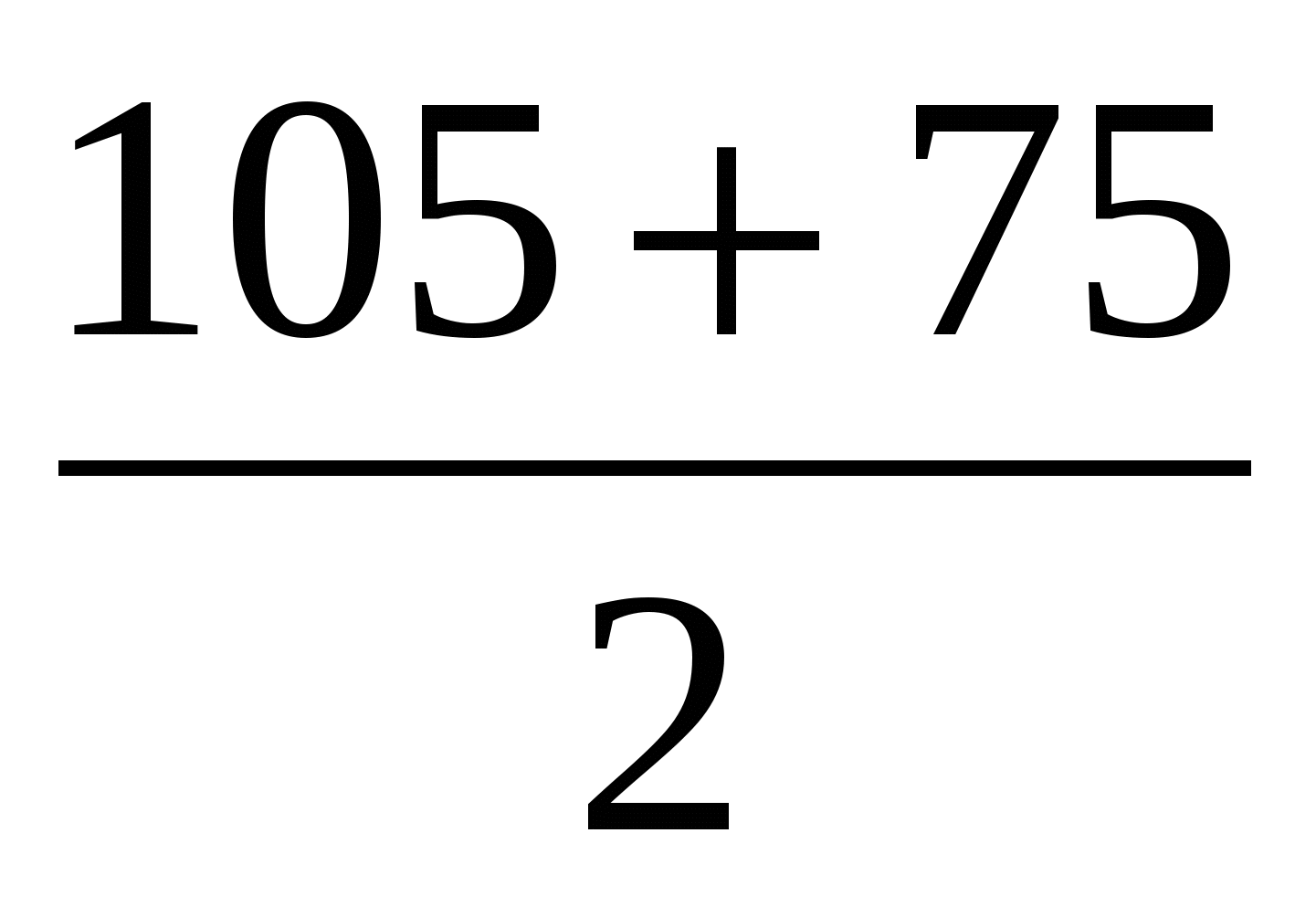 ×cos
×cos 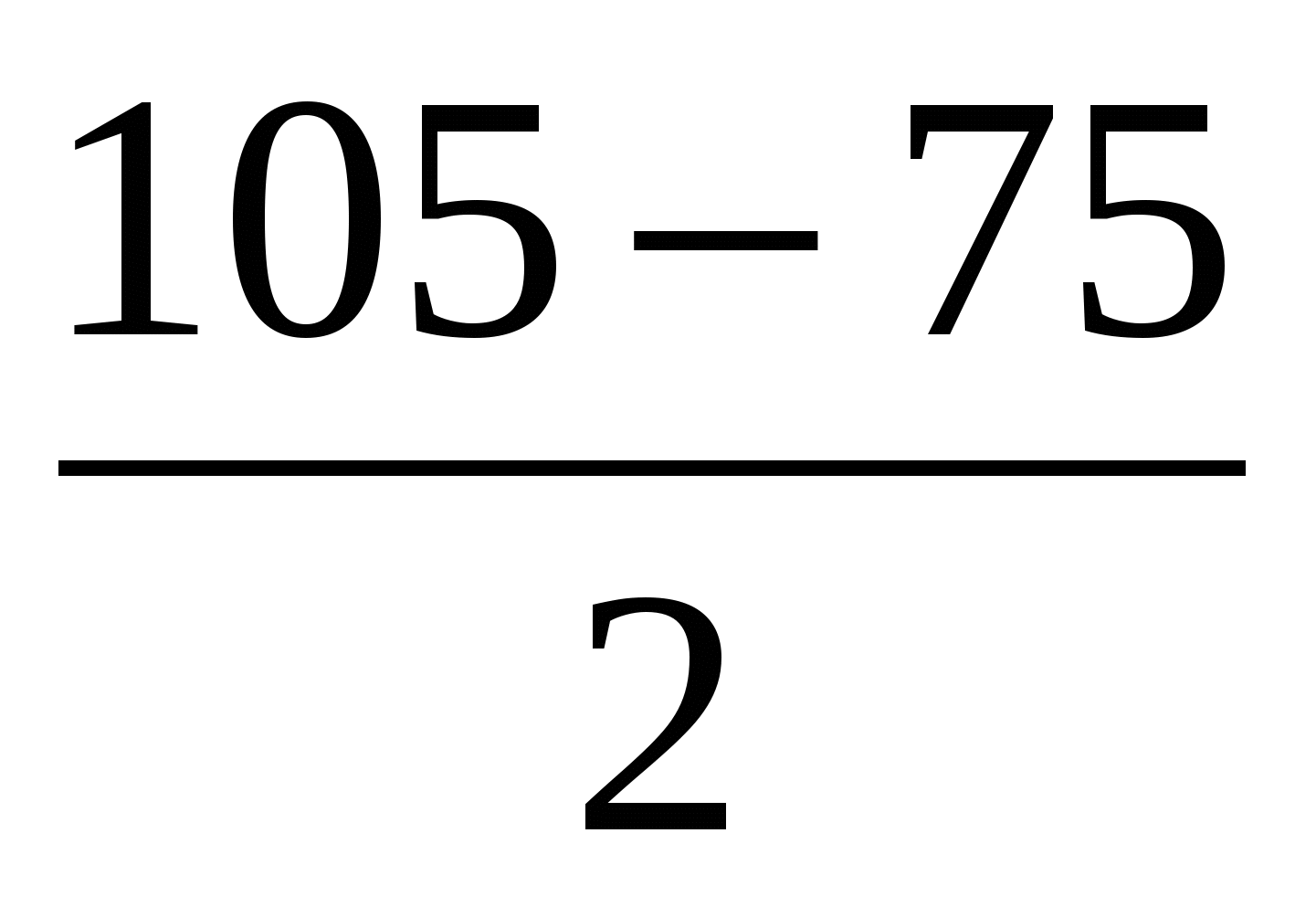 = 2 cos900 × cos150 = 2 ×0×cos15=0.
= 2 cos900 × cos150 = 2 ×0×cos15=0.
Пример 2.
Вычислить:
cos 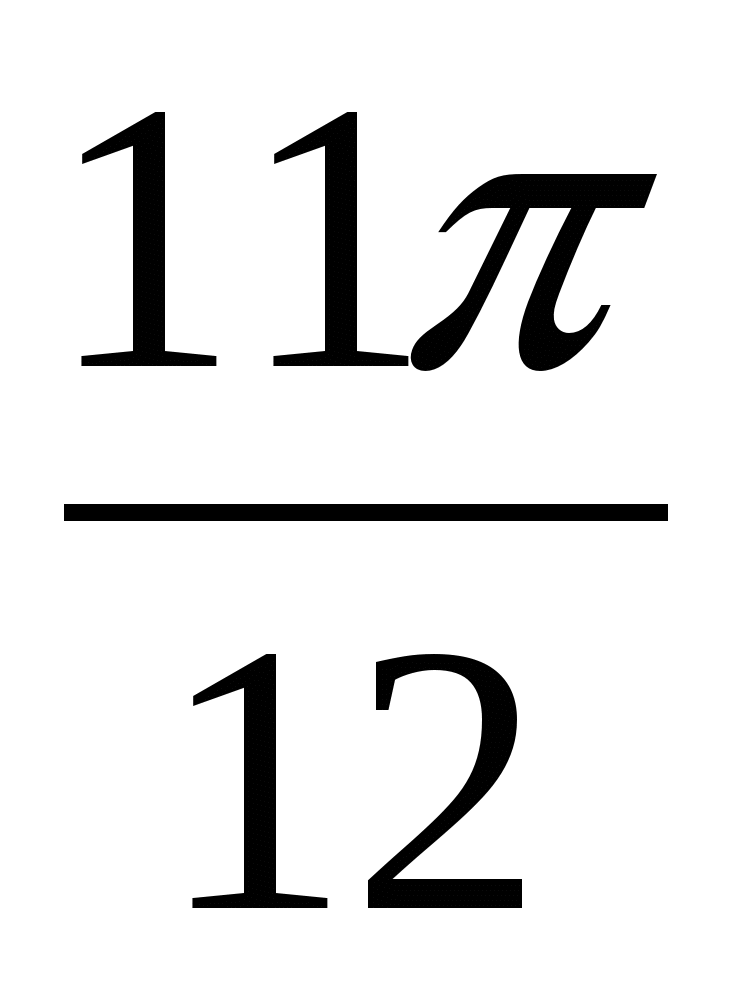 - cos
- cos 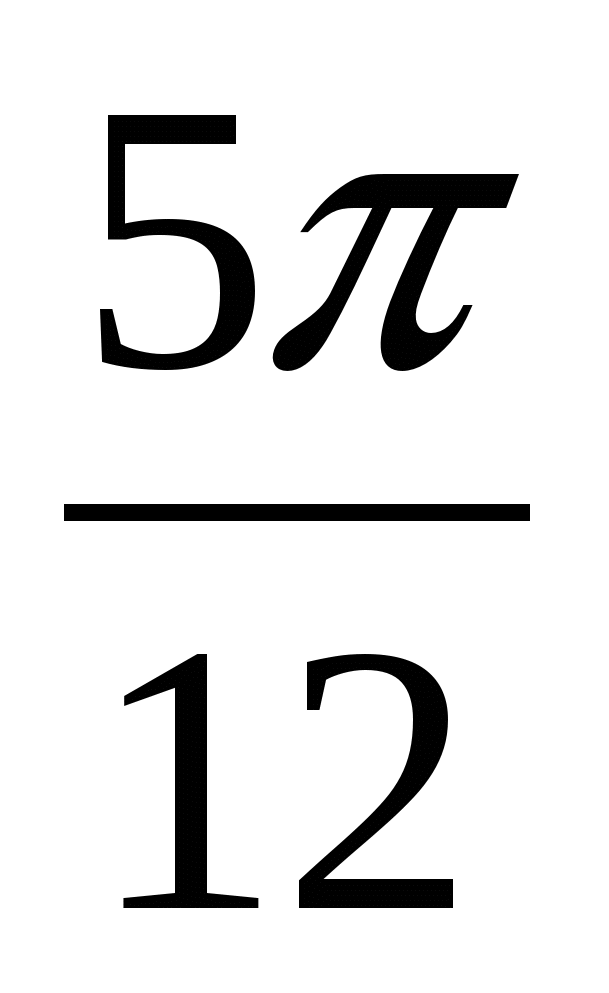 = - 2× Sin
= - 2× Sin 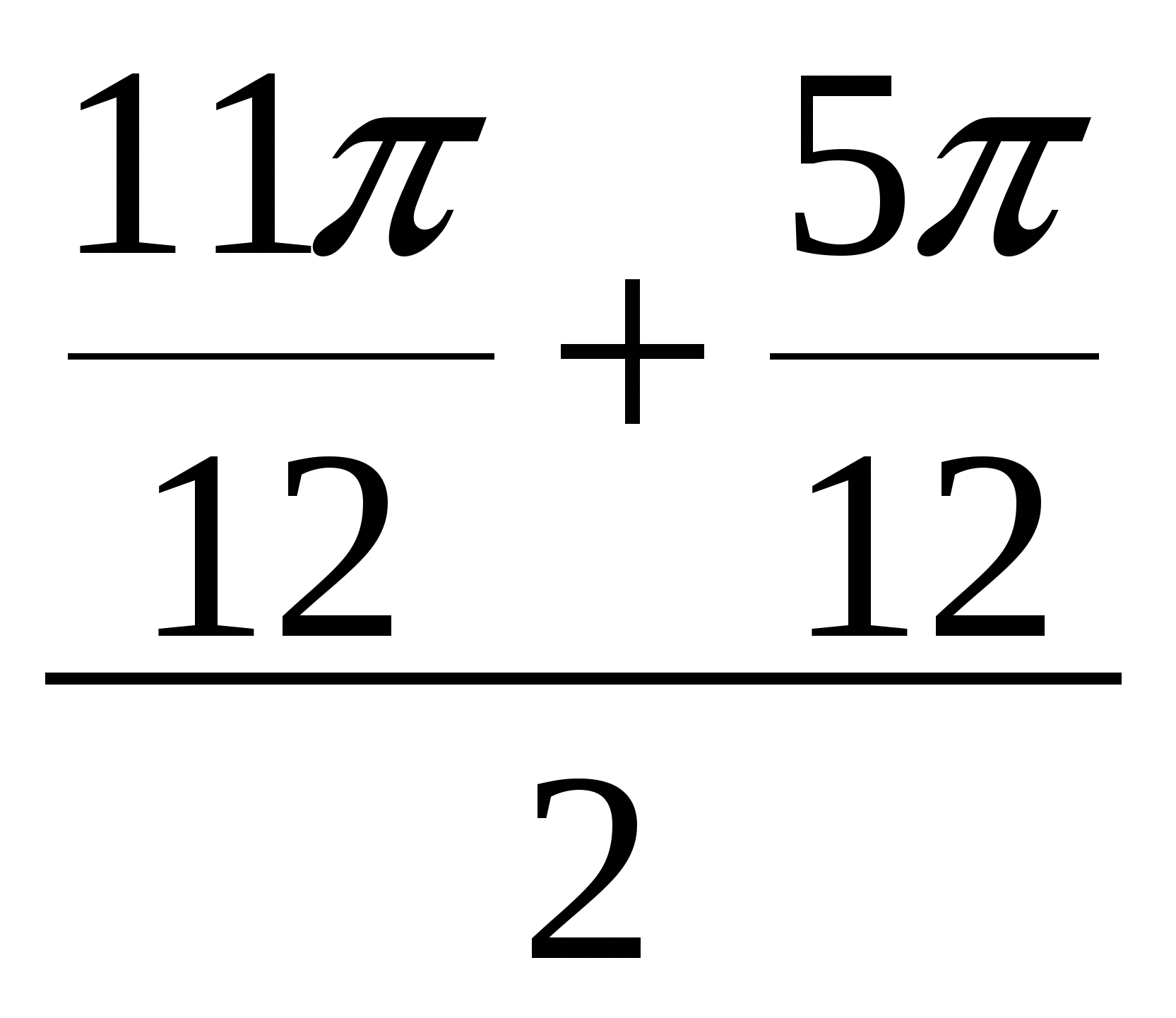 × Sin
× Sin 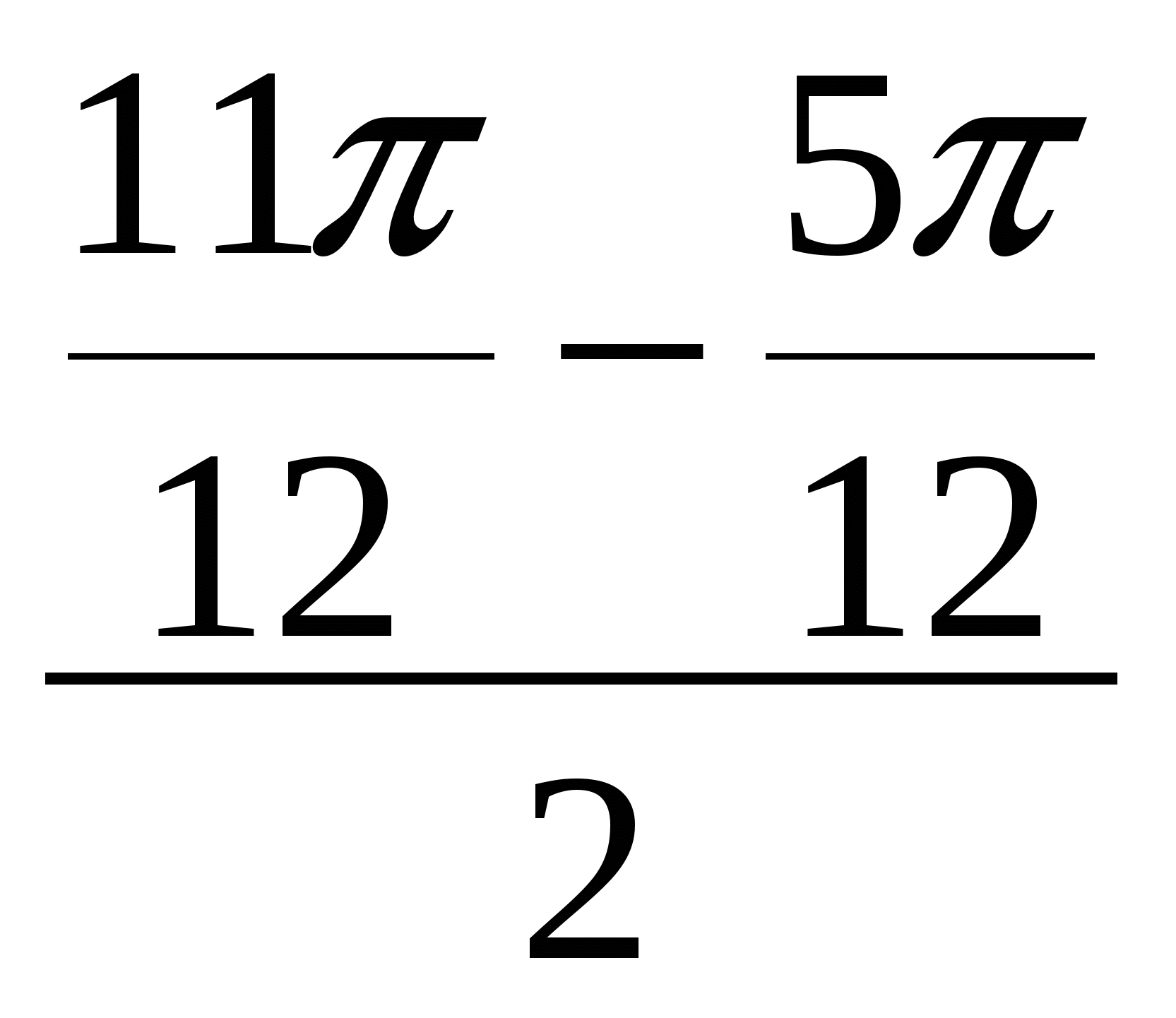 = - 2× Sin
= - 2× Sin 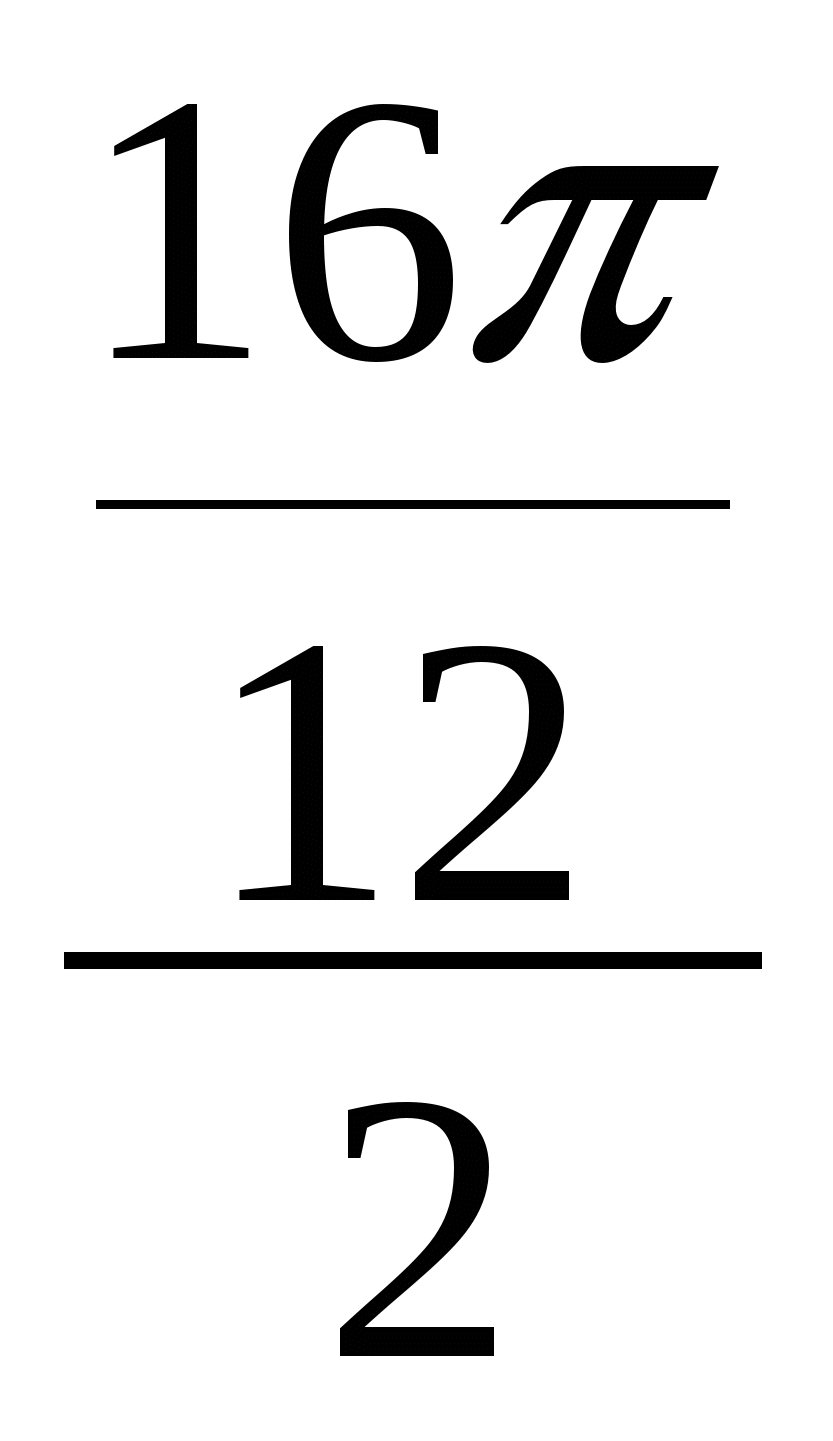 × Sin
× Sin 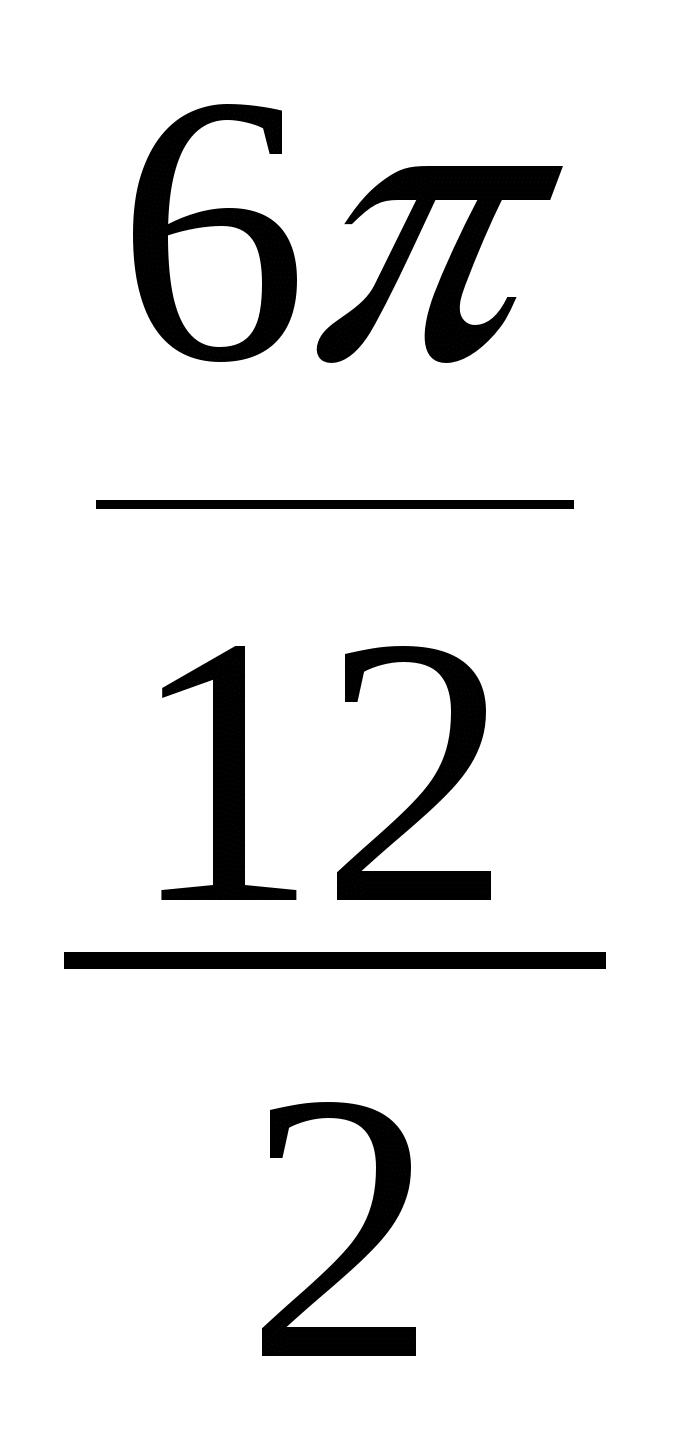 =
=
= - 2× Sin 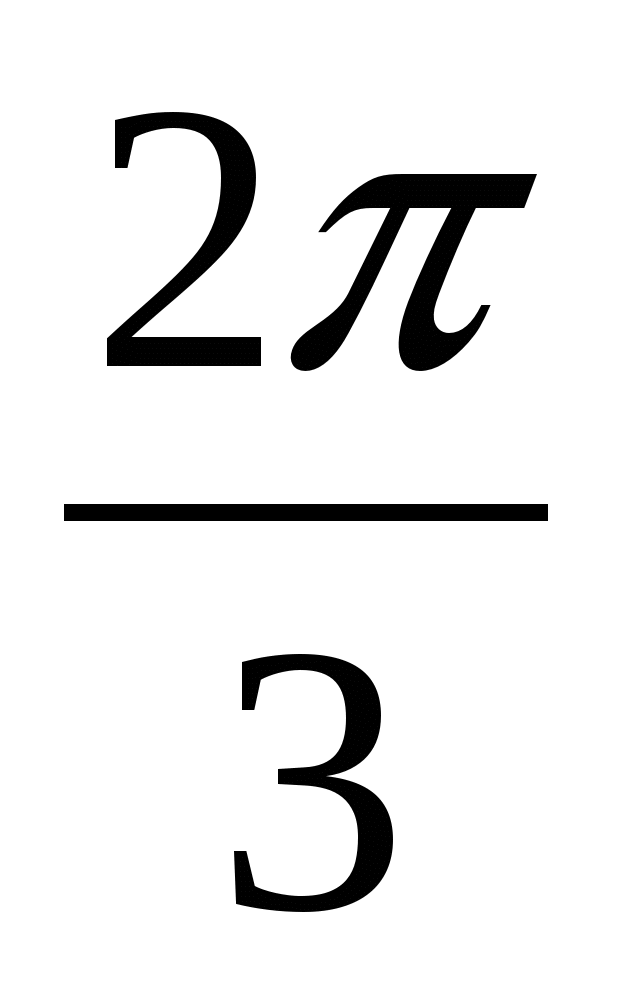 × Sin
× Sin 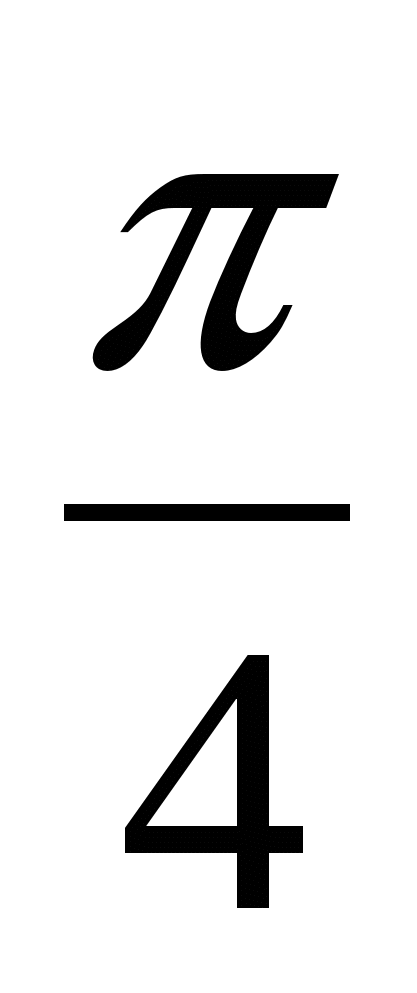 = - 2×
= - 2× 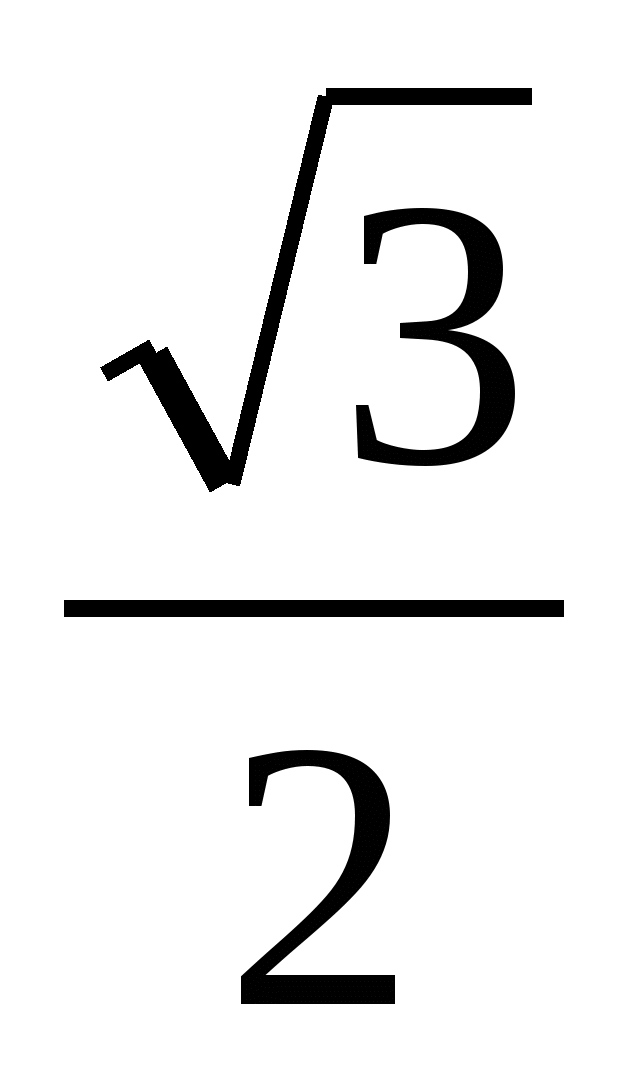 ×
× 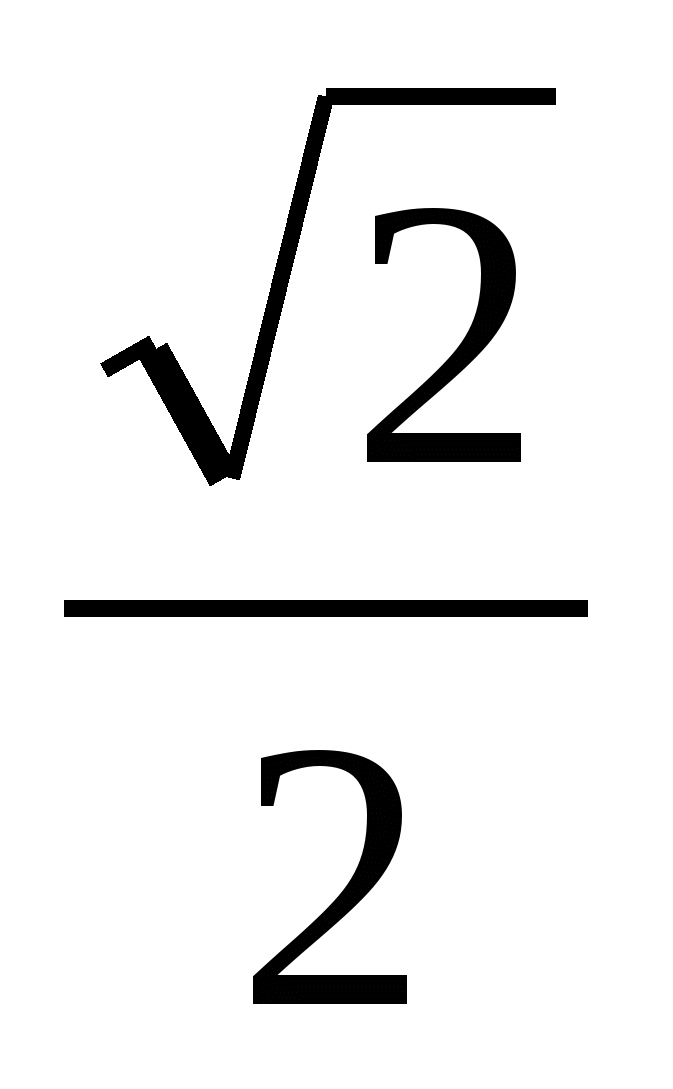 = -
= - 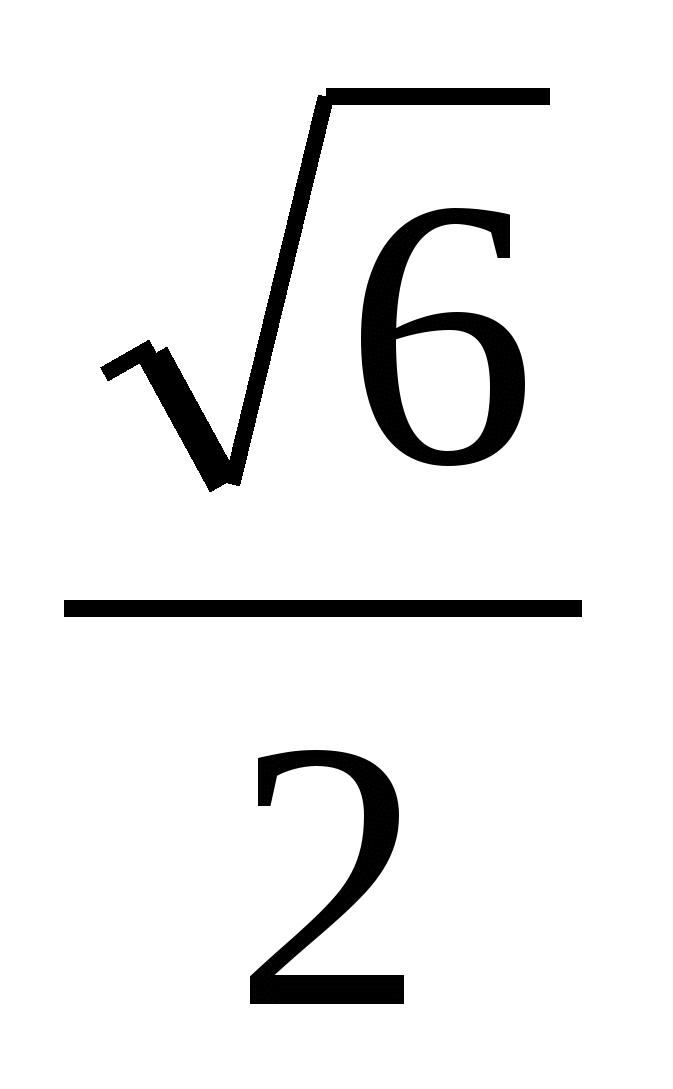 .
.
Самостоятельная работа
Вариант №1
Вариант №2
1). Вычислить:
cos 1050 - cos 750;
1).Вычислить:
cos 750 - cos 150;
2). Вычислить:
cos 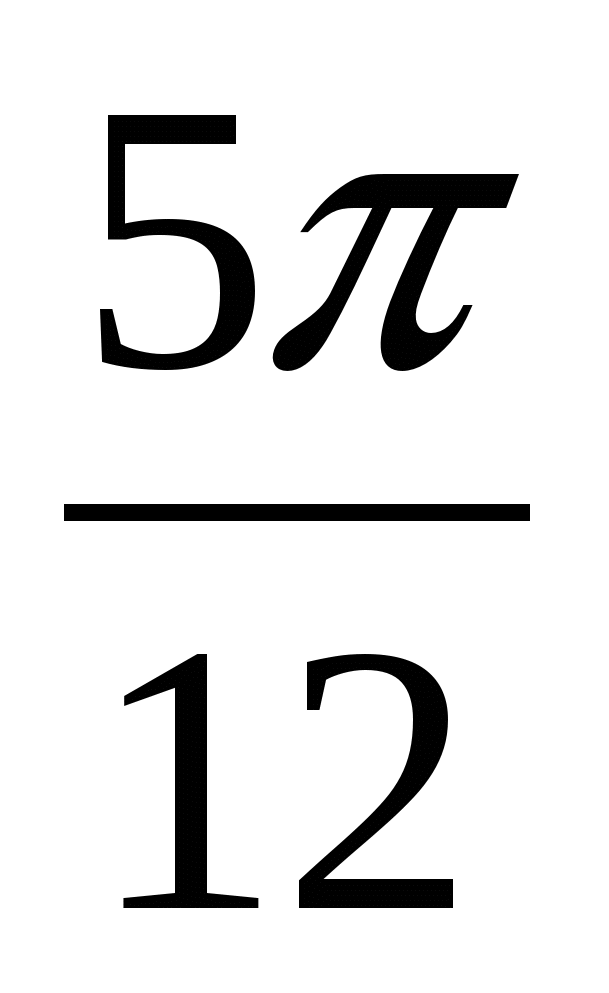 - cos
- cos 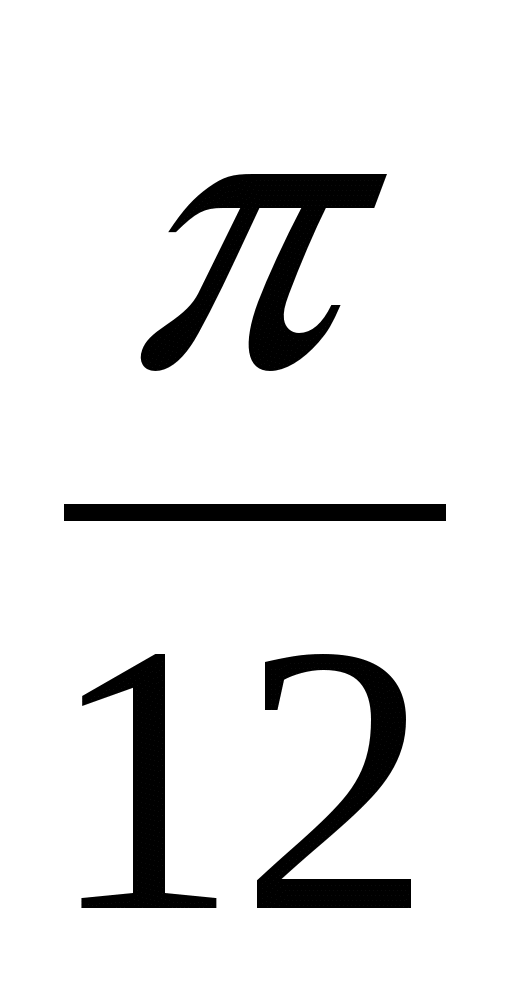 ;
;
2). Вычислить:
cos 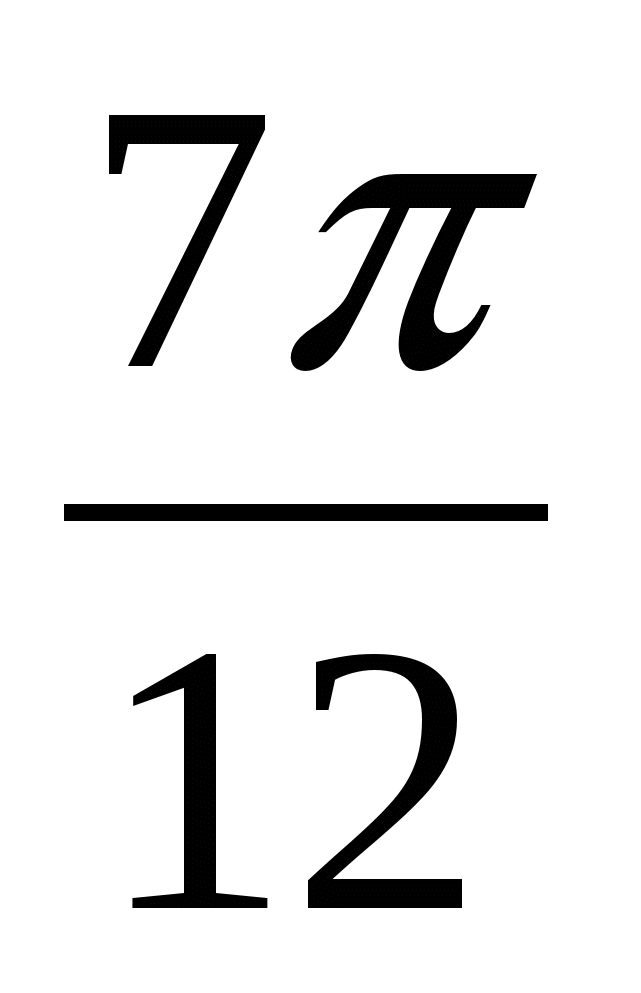 - cos
- cos 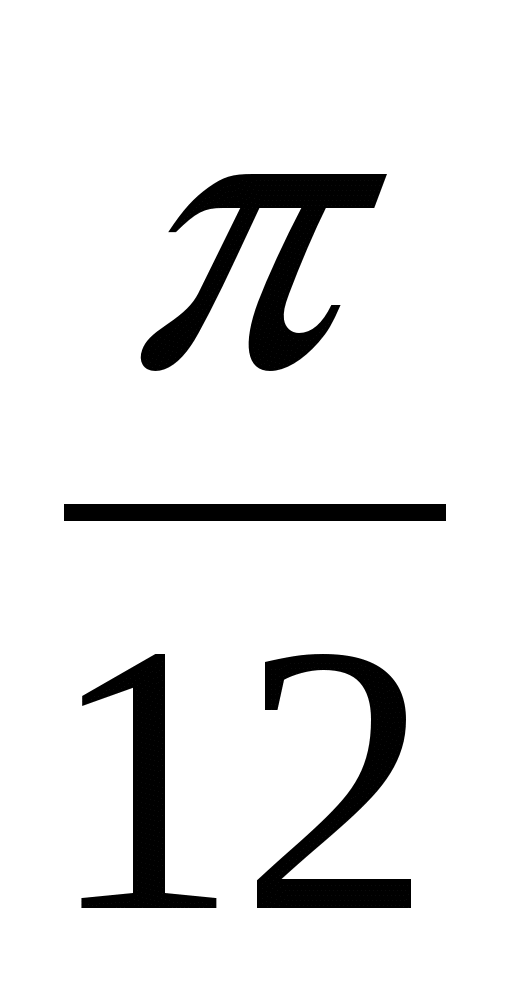 ;
;
3). Упростить выражение:
cos ( 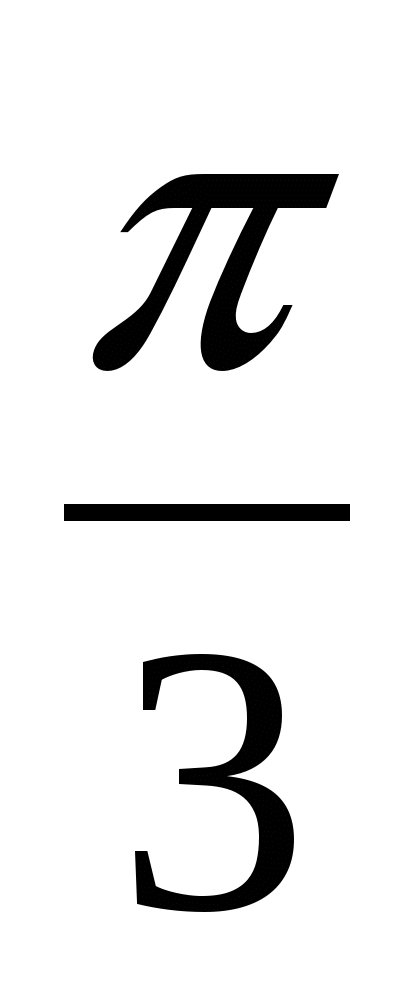 +
+ 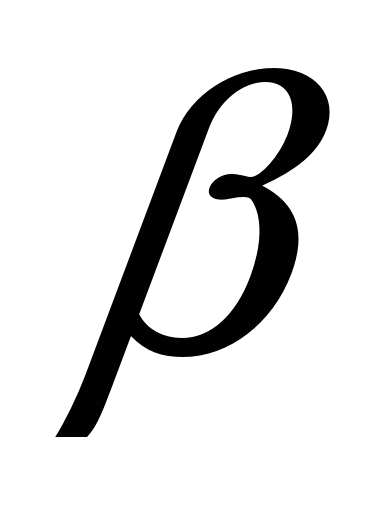 ) + cos (
) + cos ( 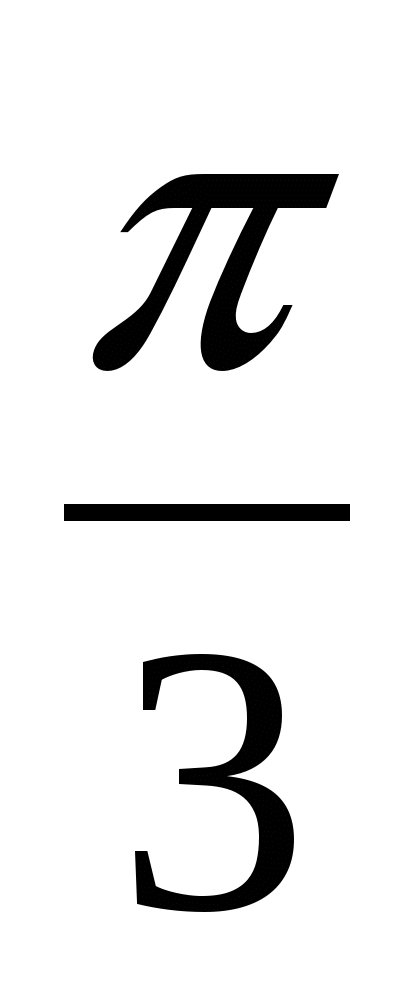 -
- 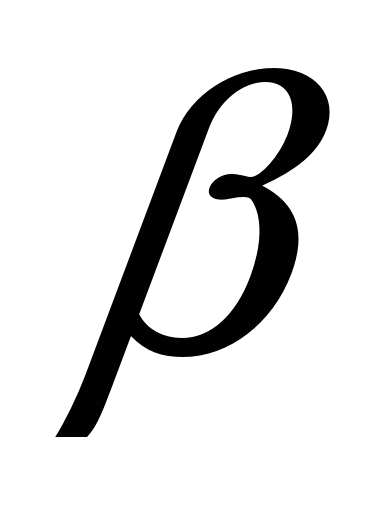 );
);
3). Упростить выражение:
cos ( 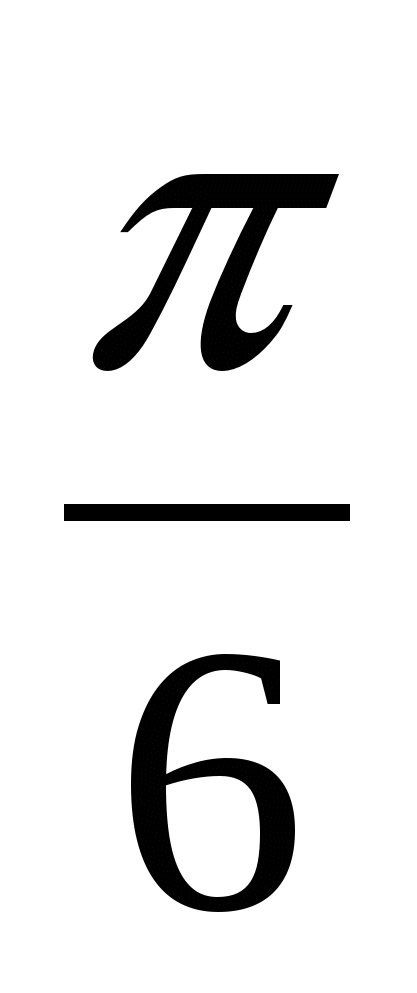 +
+ 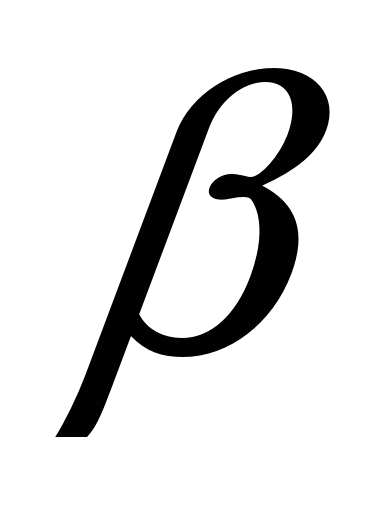 ) + cos (
) + cos ( 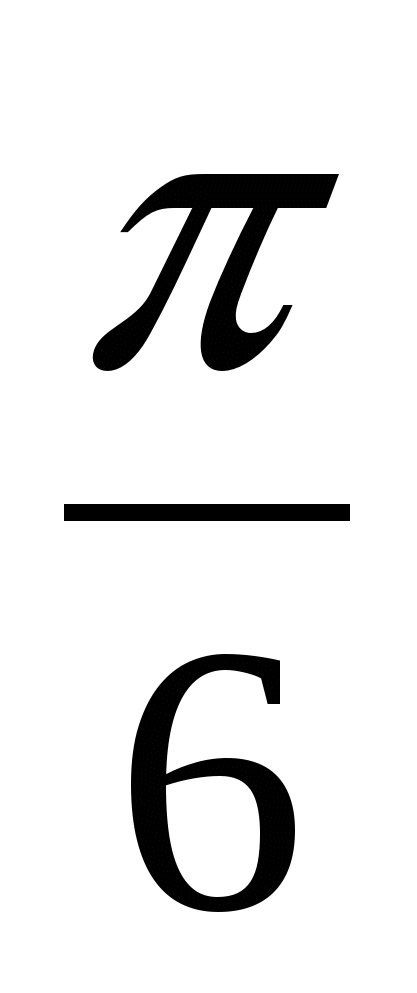 -
- 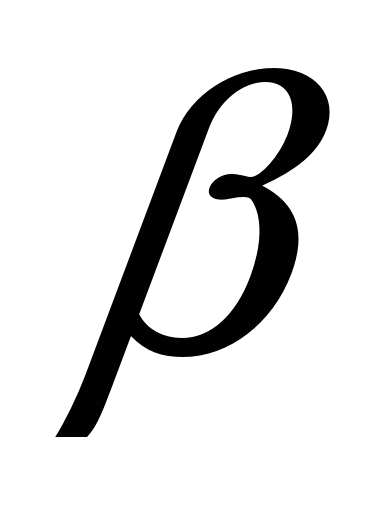 );
);
4). Преобразовать в произведение:
2 cos a + 1;
4). Преобразовать в произведение:
2 cos a + 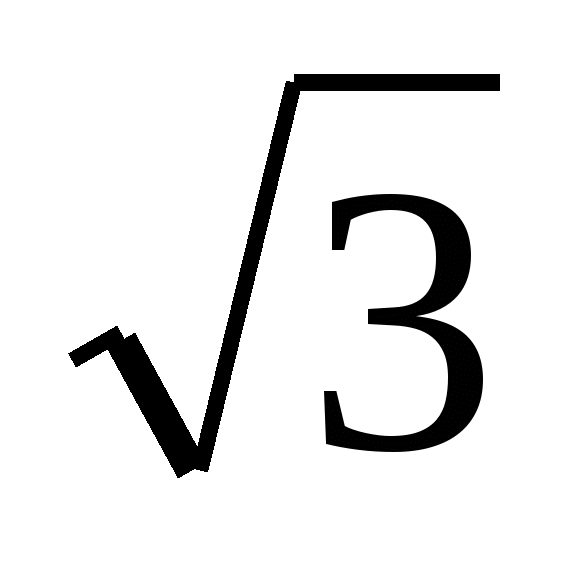 ;
;
5). Упростить выражение:
cos2 (a - 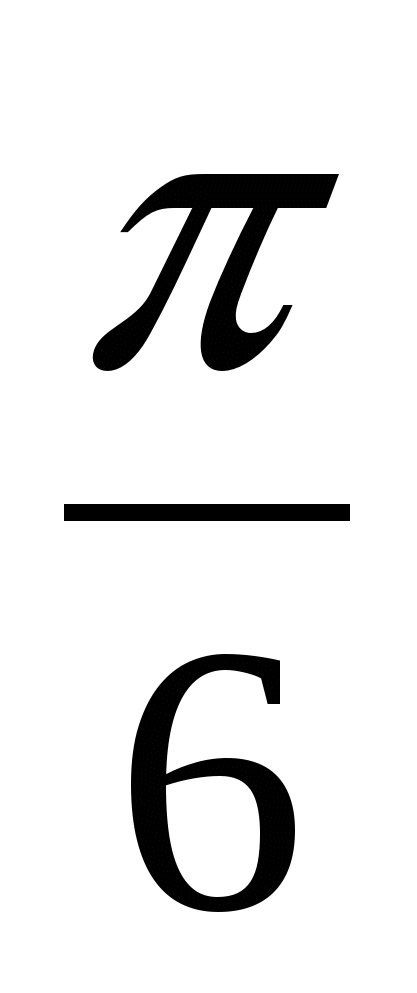 ) - cos2 (a +
) - cos2 (a + 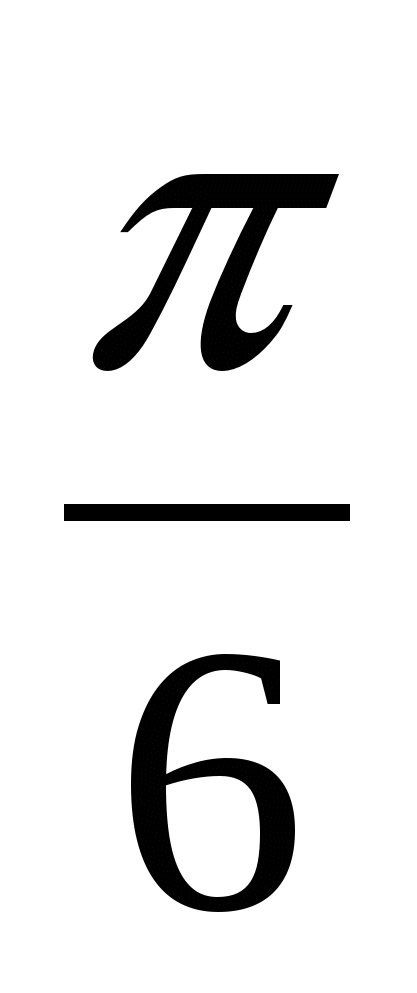 );
);
5). Упростить выражение:
cos2 (a - 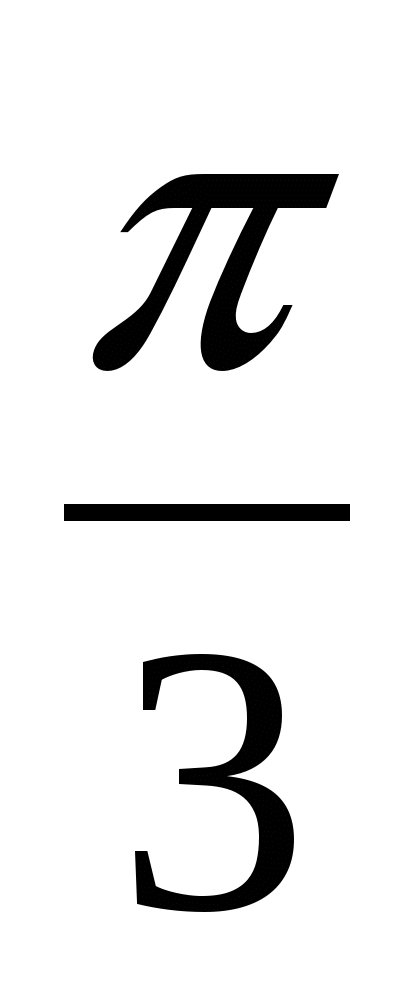 ) - cos2 (a +
) - cos2 (a + 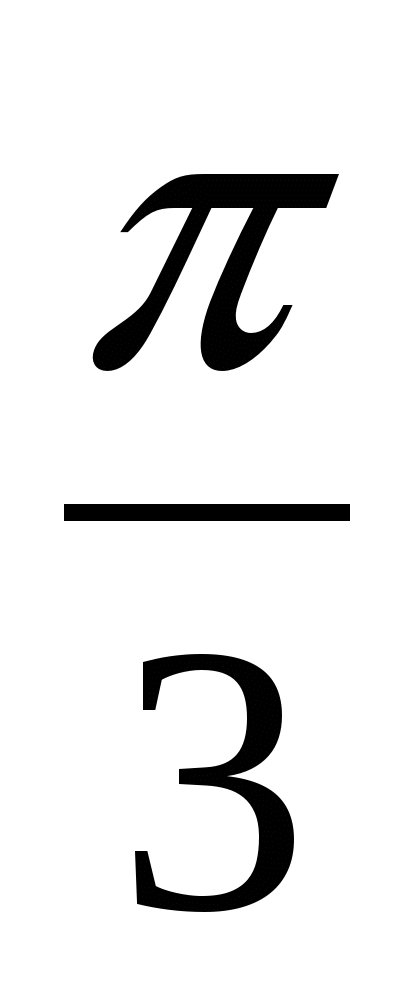 );
);
Критерии оценки:
Оценка «5» - правильные полные решения 5-ти заданий.
Оценка «4» - правильные полные решения 4-х заданий.
Оценка «3» - правильные полные решения 3-х заданий.
Дополнительное задание.
Преобразовать в произведение:
1) 1 - 2 cos a ;
2) 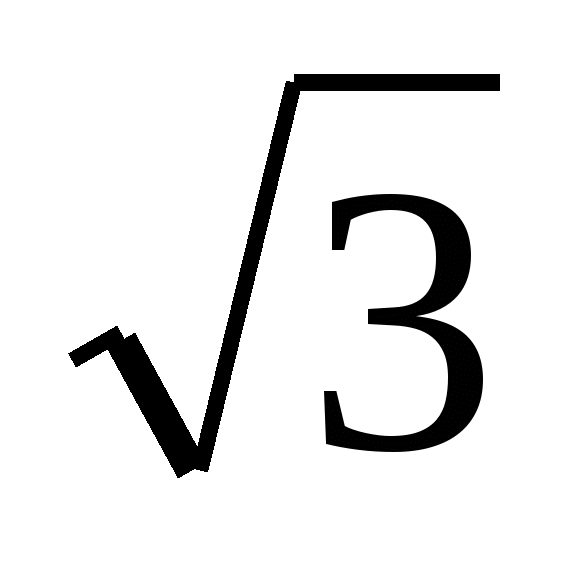 -2 cos a.
-2 cos a.
Вычислить:
cos ( 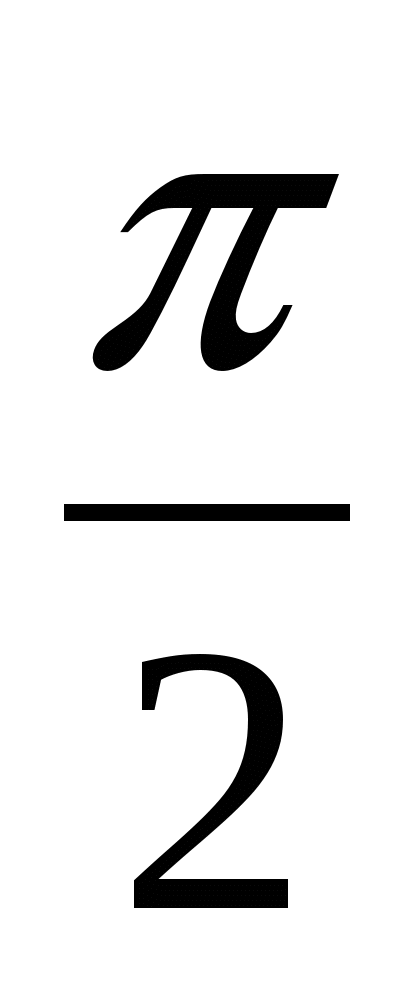 -
- 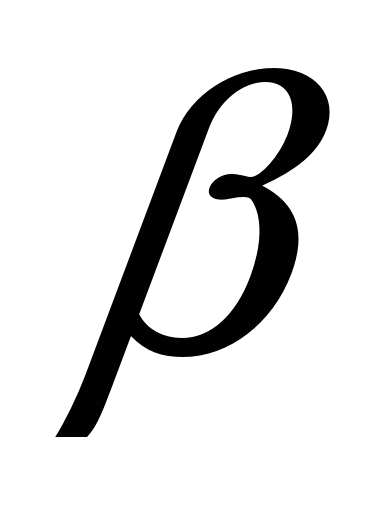 ) - cos (
) - cos ( 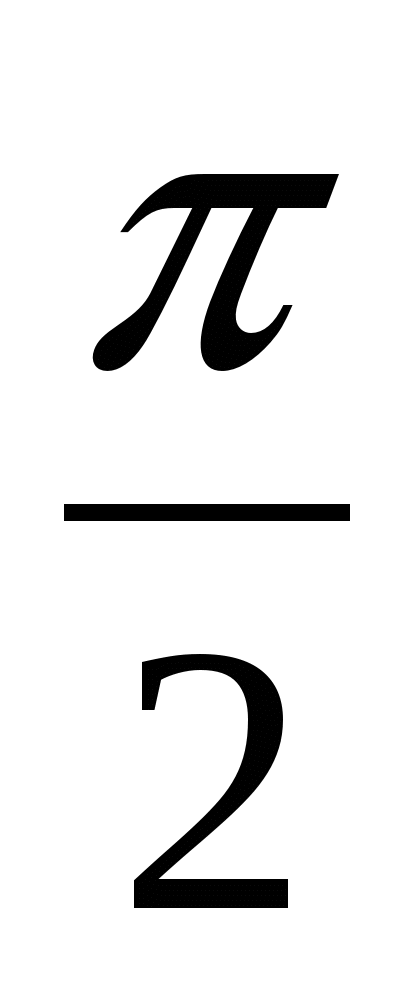 +
+  ).
).
Практическая работа № 28
