Тема: Решение иррациональных уравнений

Цель работы:

1. Повторить определение арифметического квадратного корня.

2. Отработать методы решения иррациональных уравнений.

3. Развить математическое мышление, наблюдательность, привычку аккуратно вести преобразования.

Пример:Решить иррациональное равнение:

1) 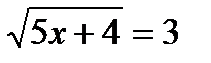2)

Решение: Проверка: Решение: Проверка:

а)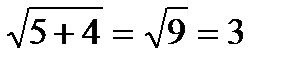

5х+4=9 3=3 х+4=3х-6 б)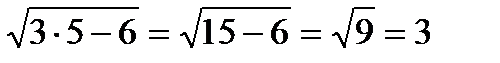

5х=9-4 х-3х=-6-4 3=3

5х=5 -2х=-10

х=1 Ответ: х=1 х=5 Ответ: х=5

3)

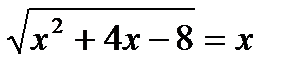
Решение: Проверка:

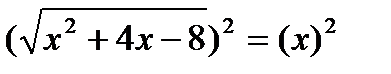
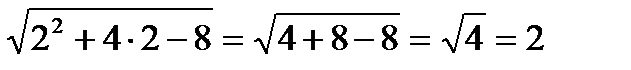
х²+4х-8=х² х=2

х²+4х-8-х²=0 2=2

4х-8=0

4х=0+8

4х=8

х=2 Ответ: х=2

Самостоятельная работа

1.

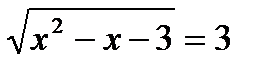
2.

3.

4.

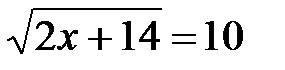
5.

6.

7.

8.

9. х-2 =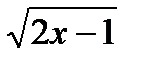

10. х+3 =

11.

12.

Практическая работа № 16

Тема: Решение иррациональных неравенств

Определение:Если в неравенство входят функции под знаком корня, то такие неравенства называют иррациональными

Неравенства вида

данное неравенство равносильно системе неравенств:

Пример:Решить неравенство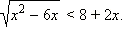

Решение:

Сразу перейдём к равносильной системе:

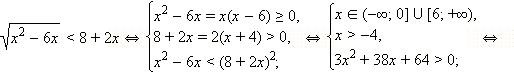
Ответ.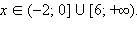

Задание 1: Закончить решение неравенства

Решение :

Перейдём к равносильной системе:

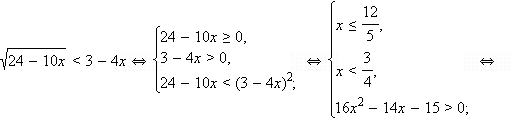
Ответ: х<-

Задание 2: Решить иррациональные неравенства:

1)

2)

Неравенства вида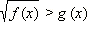

данное неравенство равносильно совокупности неравенств:

Задание 3: Решить иррациональные неравенства:

1)

2)

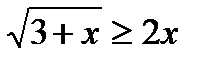
Неравенства вида

данное неравенство равносильно системе неравенств:

Пример:Решить неравенство

Решение:

Перейдём к равносильной системе:

Решая эту систему методом интервалов, сразу получаем:

Ответ.

Неравенство вида >

данное неравенство равносильно системе неравенств:

> →

Задание 4: Решить иррациональные неравенства:

1)

2)

Проверь себя!

Решить иррациональное неравенство:

1. >3

2. >4

3. <1

4. >4

5.

6.

Практическая работа № 17

Тема: Степень с рациональным показателем

Цель:научиться выполнять преобразование алгебраических, рациональных, иррациональных, степенных выражений с использованием формул сокращенного умножения, основных свойств корней и степеней.

Теоретические сведения.

Корни натуральной степени из числа, их свойства.

Корень n – степени: , n -показатель корня, а –подкоренное выражение

Если n – нечетное число,то выражение 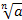имеет смысл при а

Если n – четное число,то выражение имеет смысл при

Арифметический корень:

Корень нечетной степени из отрицательного числа:

Основные свойства корней

1. Правило извлечения корня из произведения: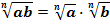

2. Правило извлечения корня из дроби: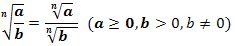

3. Правило извлечения корня из корня:

4. Правило вынесения множителя из-под знака корня: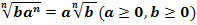

5. Внесение множителя под знак корня:

,

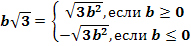6. Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число.

Правило возведения корня в степень.

Степень с натуральным показателем

= ,a – основание степени, n– показатель степени

Свойства:

1.

2.

3.

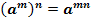
4.

5.

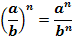
6. Если

Степень с целым показателем

1.

2.

3.

4. По определению:

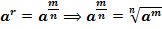
Пример 1. Упростите выражение .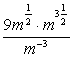

Решение

Применим свойства степеней (умножение степеней с одинаковым основанием и деление степеней с одинаковым основанием): .

Ответ: 9m⁷ .

Пример 2.Сократить дробь:

Решение.Так область определения дроби все числа, кроме х ≠ 1 и х ≠ -2.Вместе с тем .Сократив дробь, получим 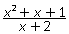.Область определения полученной дроби: х ≠ -2, т.е. шире, чем область определения первоначальной дроби. Поэтому дроби и 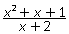равны при х ≠ 1 и х ≠ -2.

Самостоятельная работа

Вариант 1

1. Упростите выражение:

2. Найдите значение выражения:

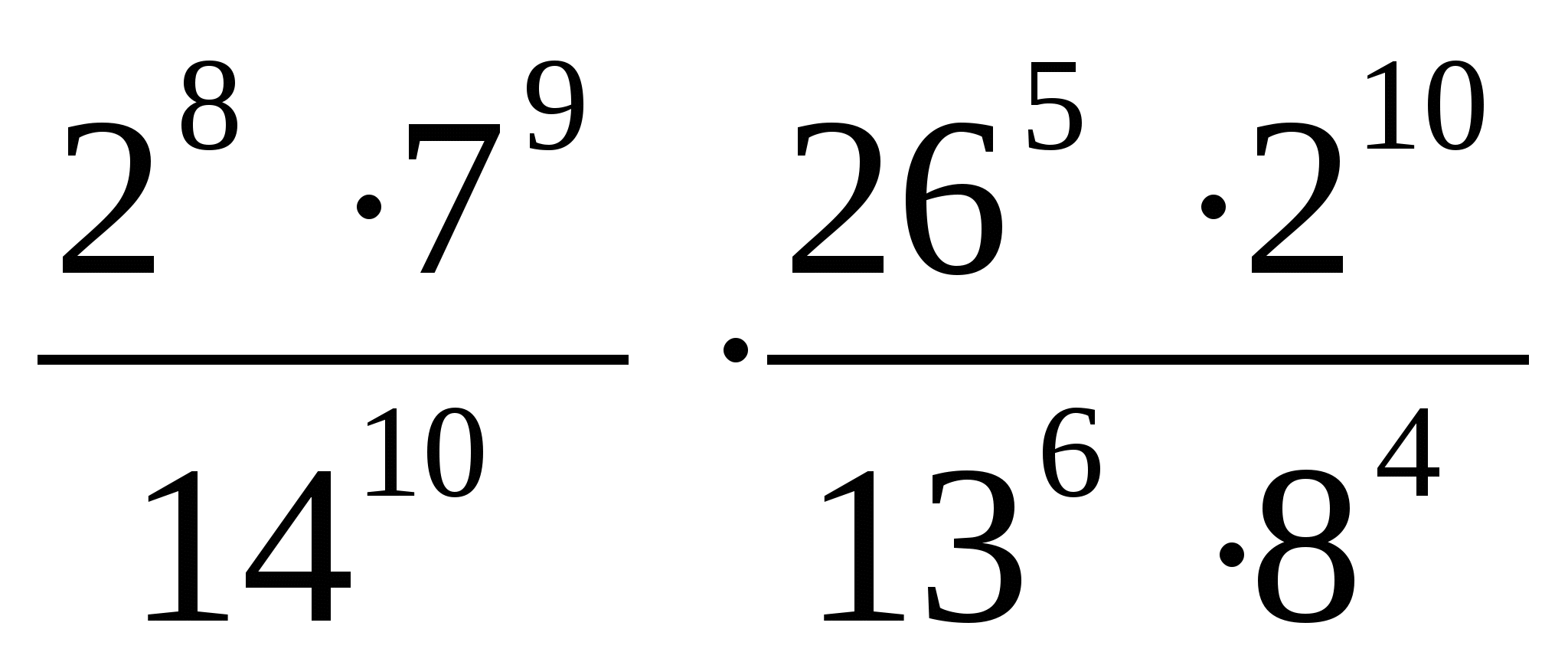
3. Представьте степень с дробным показателем в виде корня

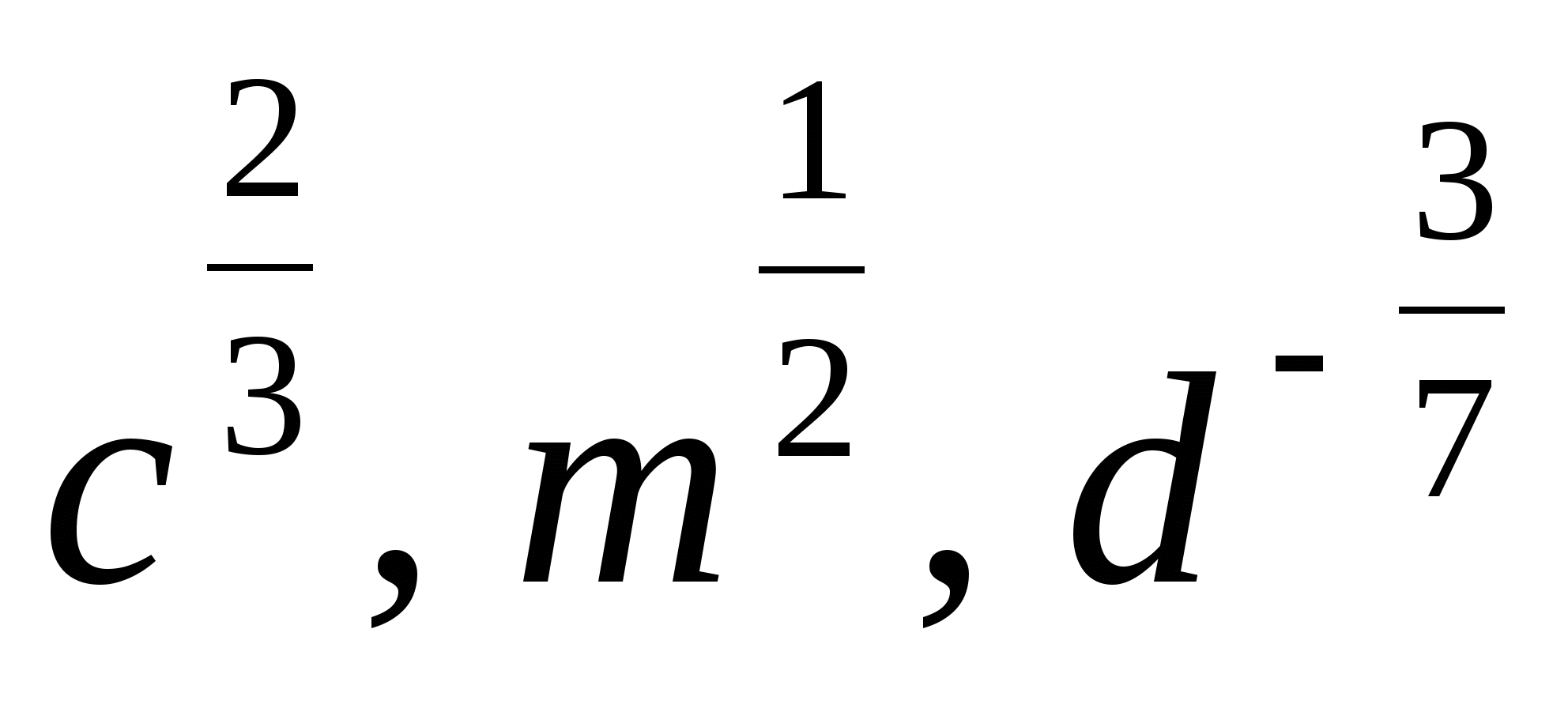
4. Привести указанное выражение к виду 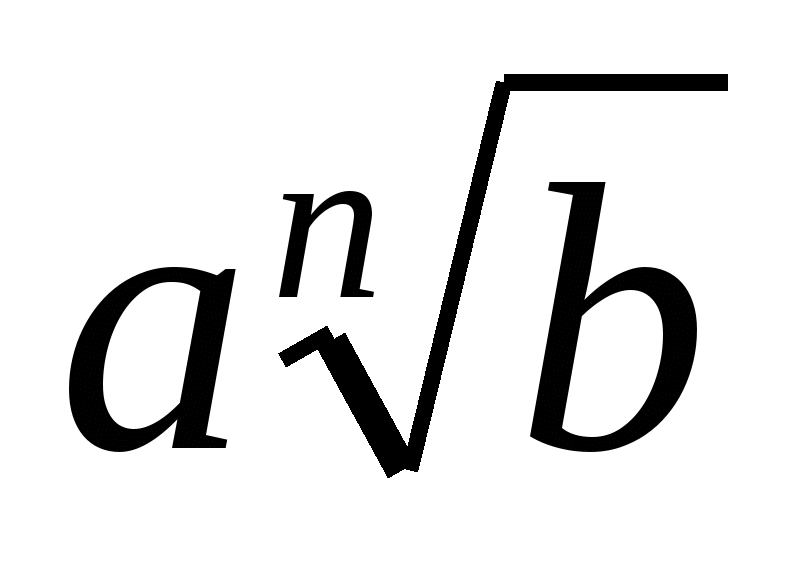, где а -рациональное число, b – натуральное число

,

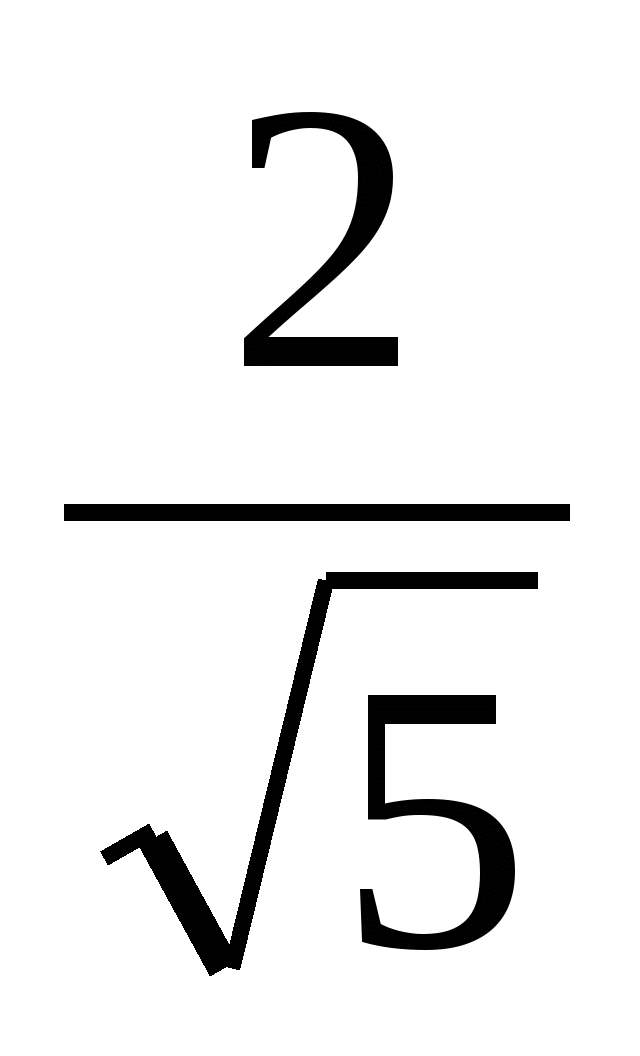
5. Упростить:

;

6. Замените арифметические корни степенями с дробным показателем

, ,

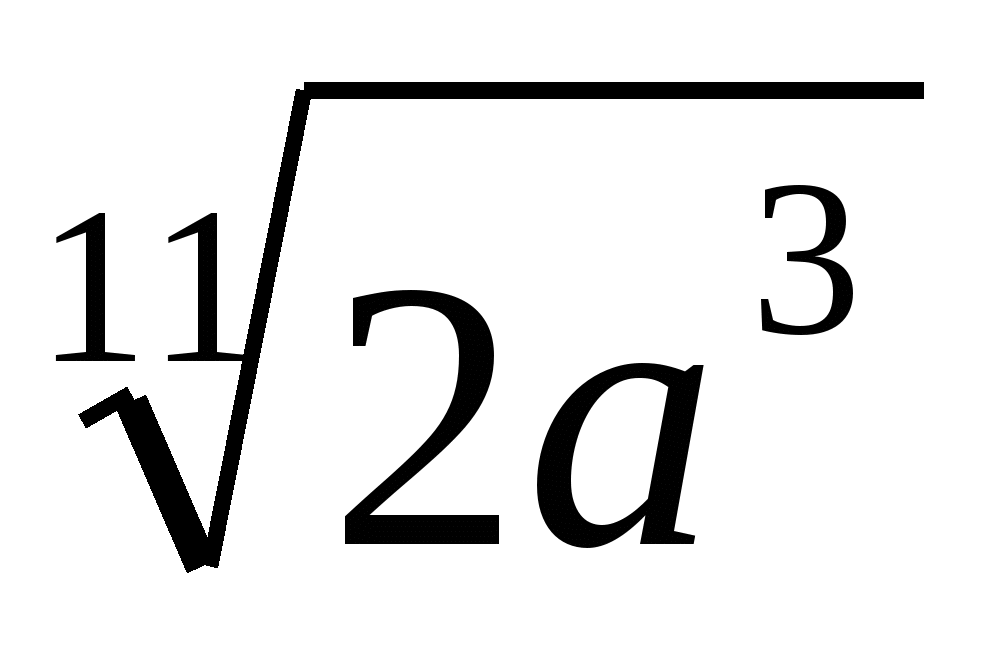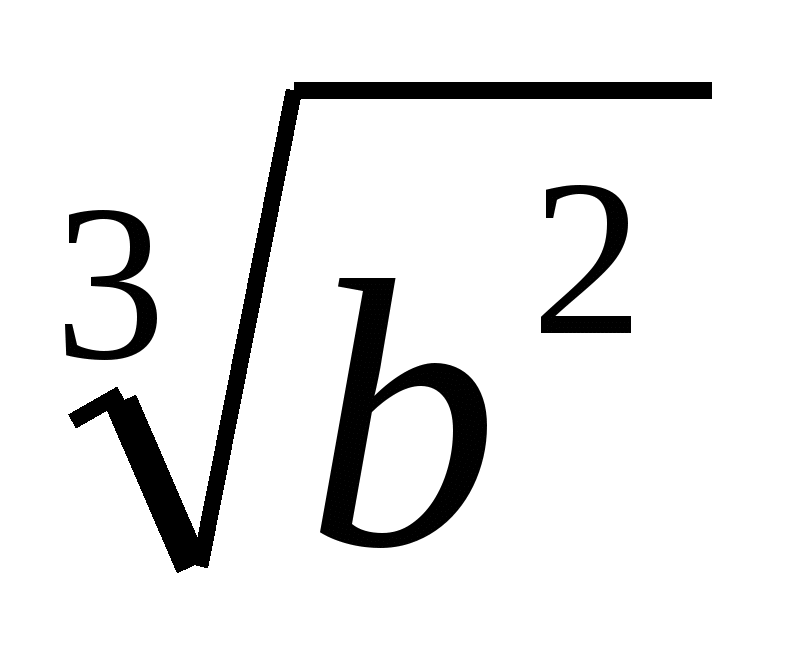
7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня

8. Выполните действие:

9. Сократите дробь

10. Выполните действие

Вариант 2

1. Упростите выражение:

2. Найдите значение выражения:

3. Представьте степень с дробным показателем в виде корня

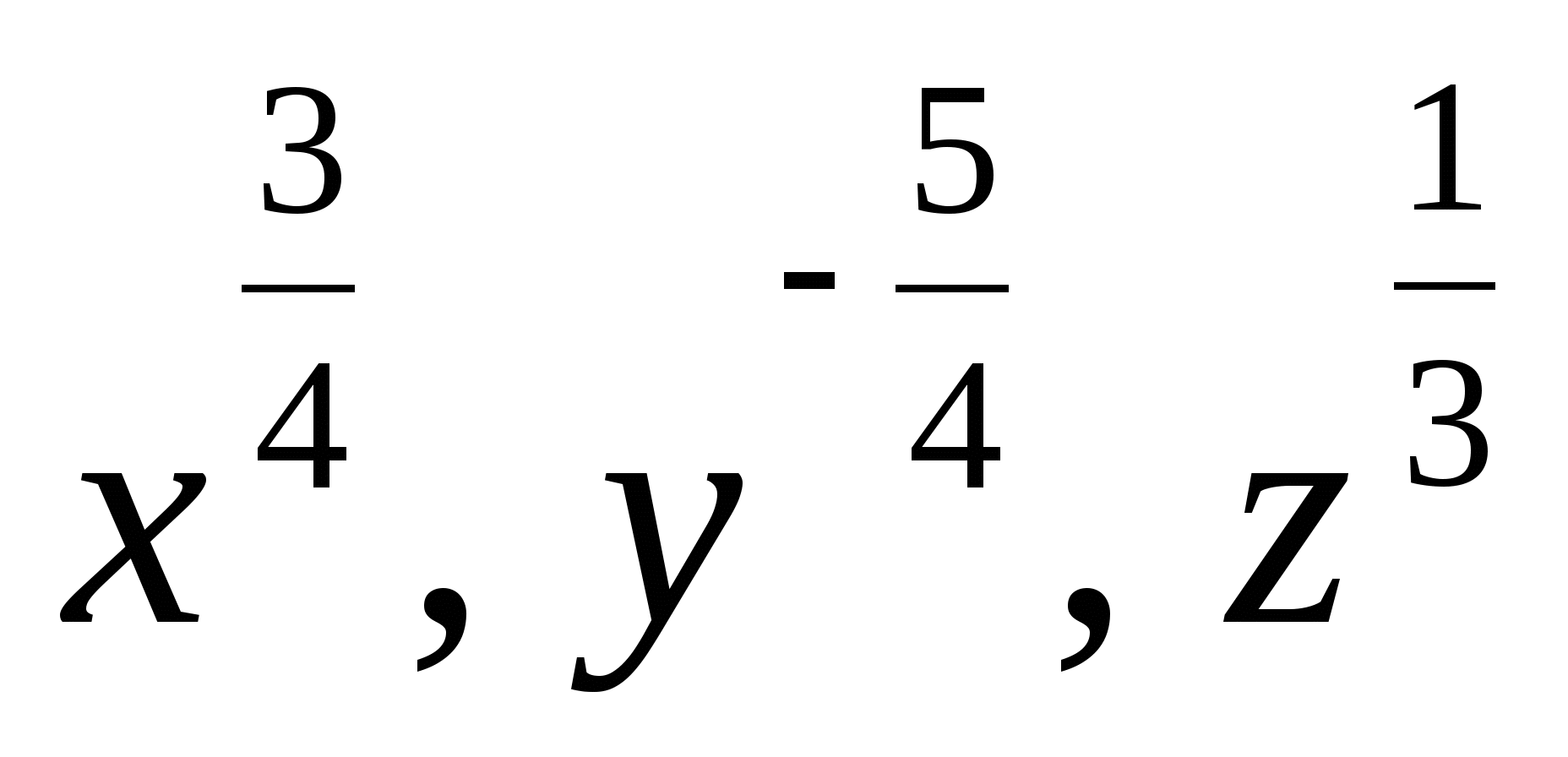
4. Привести указанное выражение к виду 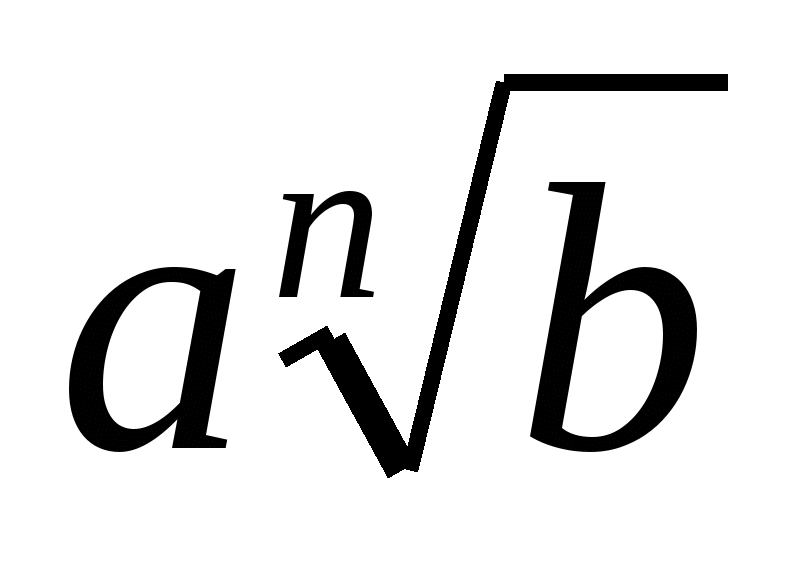, где а- рациональное число, b – натуральное число

,

5. Упростить:

;

6. Замените арифметические корни степенями с дробным показателем

, ,

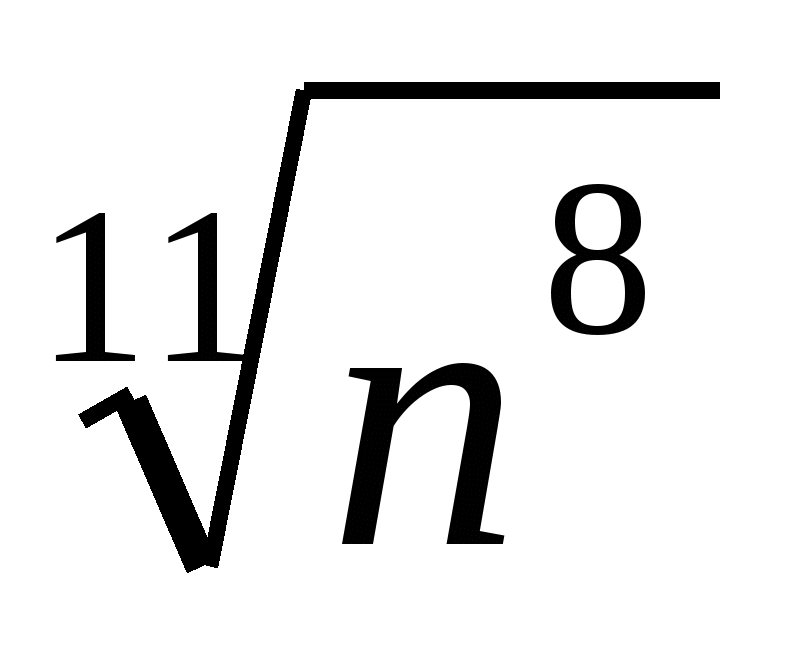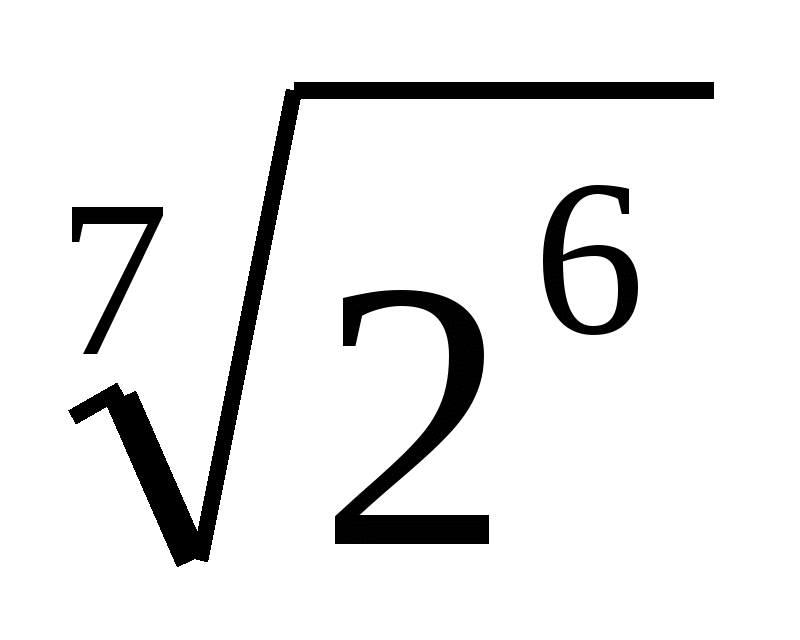7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня

10. Выполните действие:

8. Сократите дробь

9. Выполните действие

Вариант 3

1. Выполните действие:

2. Найдите значение выражения:

3. Представьте степень с дробным показателем в виде корня

4. Привести указанное выражение к виду 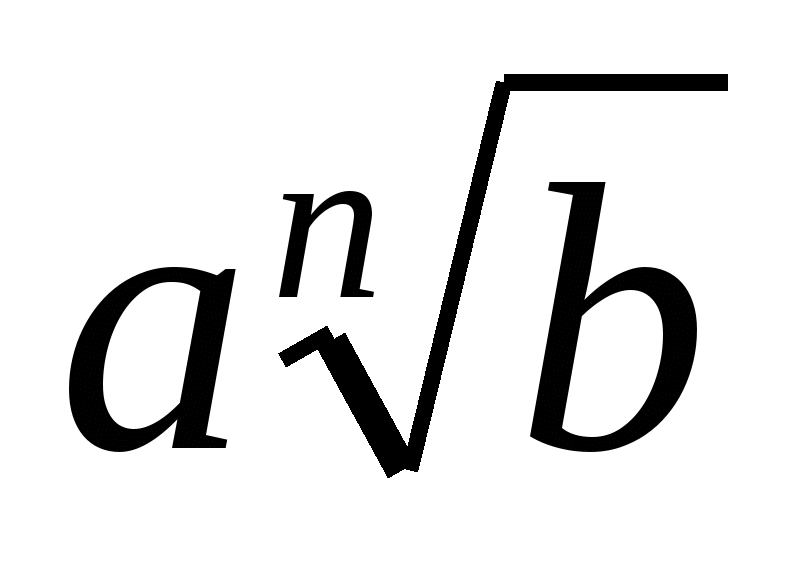, где а -рациональное число, b – натуральное число

,

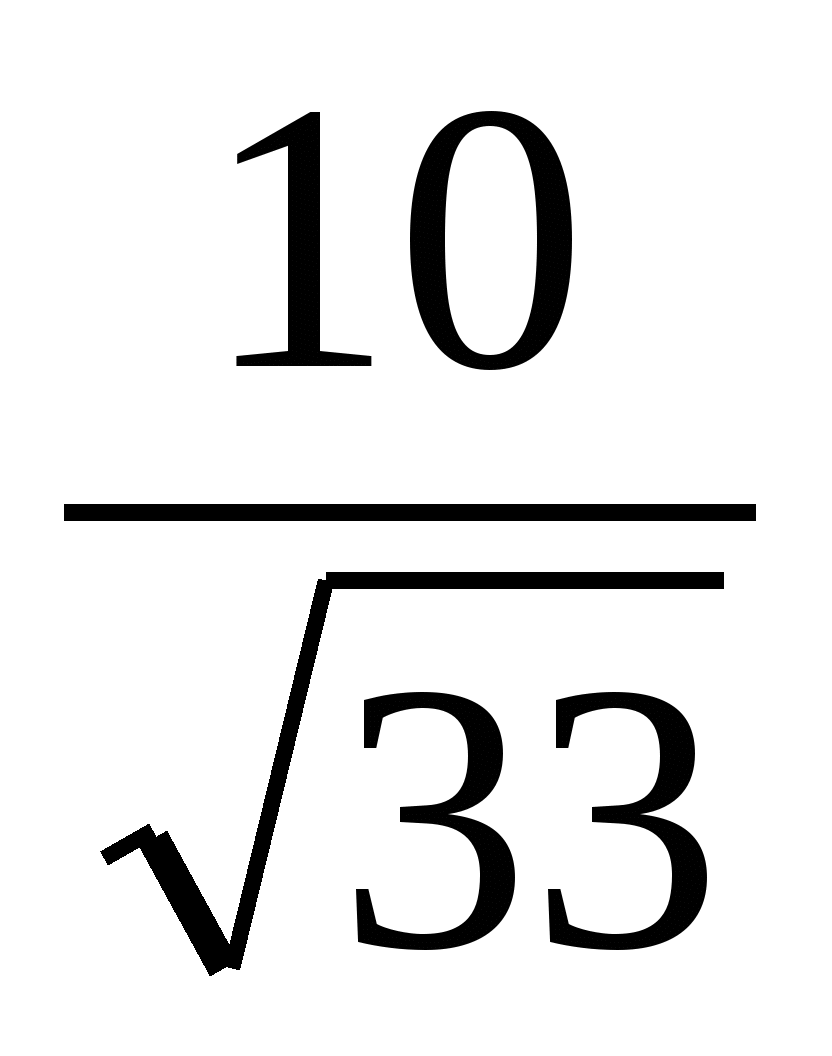
5. Упростить:

;

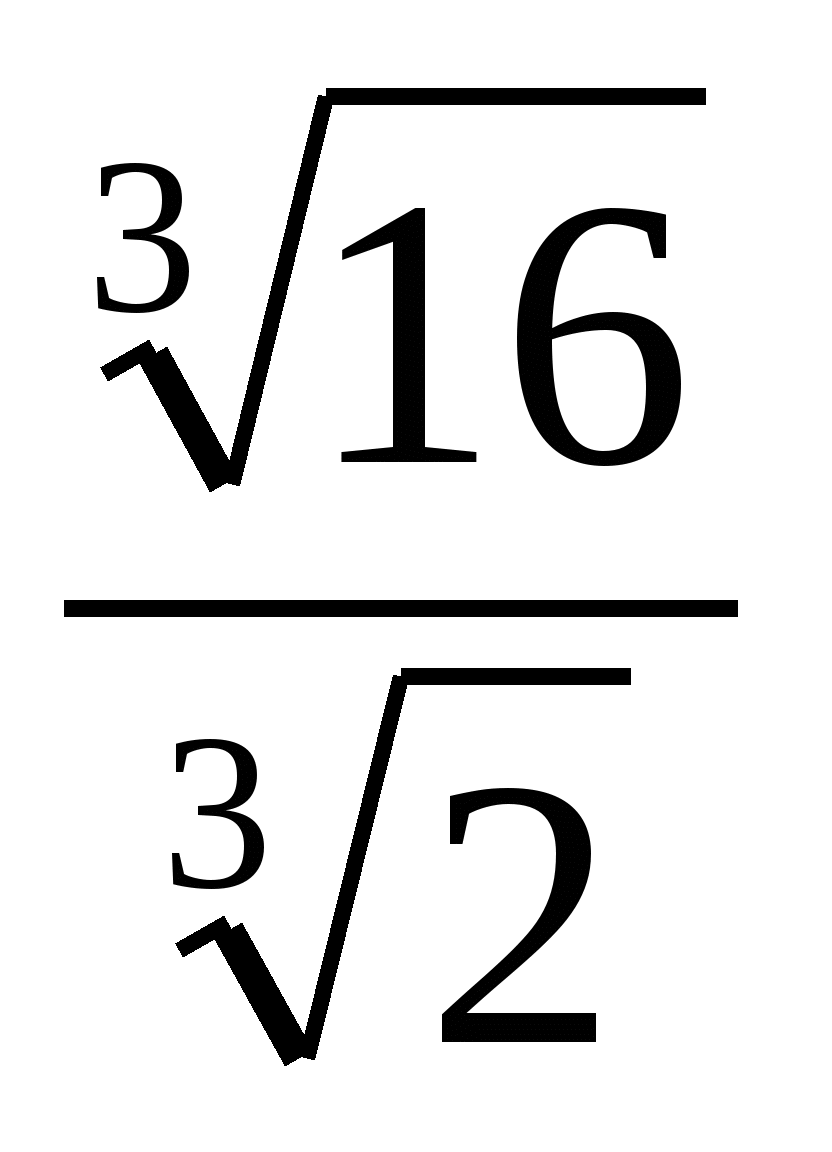6. Замените арифметические корни степенями с дробным показателем

, ,

7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня

10. Выполните действие:

8. Сократите дробь

9. Выполните действие

Практическая работа №18