Определение рациональных чисел как классов эквивалентности
Определение: 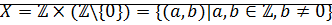
Будем говорить, что пара 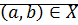 эквивалентна паре
эквивалентна паре 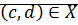 , если
, если 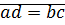 . Обозначается
. Обозначается 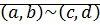 .
.
Пример: 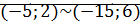
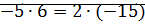
Теорема: Отношение « 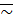 » определенное таким образом, является отношением эквивалентности.
» определенное таким образом, является отношением эквивалентности.
Доказательство: 1) Рефлексивность: 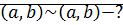
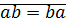
2) Симметричность: 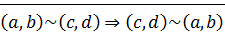 ?
?
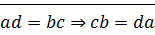
3) Транзитивность: 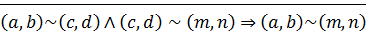
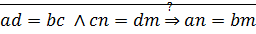
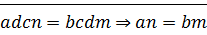 ⊠
⊠
Свойство: 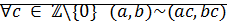
Доказательство: 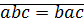 ⊠
⊠
Следствие: 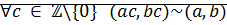
Доказательство: симметрия относительно « 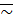 » ⊠
» ⊠
Определение: рациональными числами будем называть классы эквивалентности
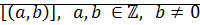
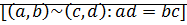
Обозначения: 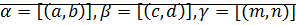
Множество 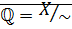
Пример: 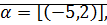
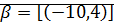 ,
, 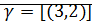
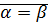 ,
, 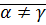
Определение суммы рациональных чисел и его корректность. Аддитивная абелева группа рациональных чисел
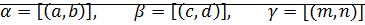
Определение: Суммой рациональных чисел 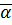 и
и 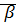 называется рациональное число
называется рациональное число
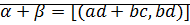
Пример: 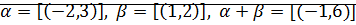
Теорема (корректность определения): Сумма рациональных чисел не зависит от выбора пар, которые определяют слагаемые.
Доказательство: 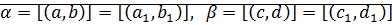
докажем: 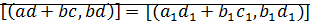
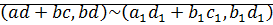
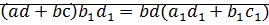
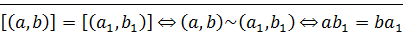
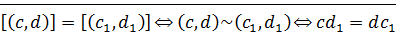
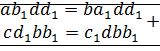
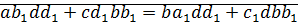
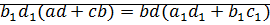
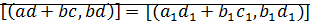 ⊠
⊠
Теорема (коммутативность сложения): 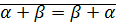
Доказательство: 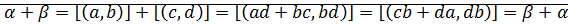
Теорема (ассоциативность сложения): 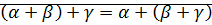
Доказательство:
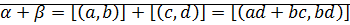
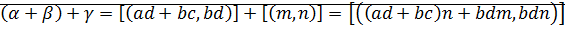
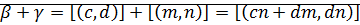
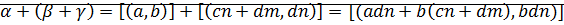 ⊠
⊠
Теорема:Множество рациональных чисел имеет нейтральный элемент относительно сложения: 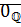 :
: 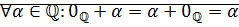 , где
, где 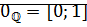
Доказательство: 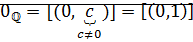
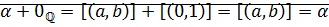 ⊠
⊠
Теорема: Противоположным относительно сложения для элемента 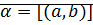 является число
является число 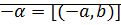
Доказательство:
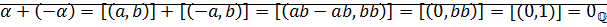 ⊠
⊠
Следствие: 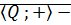 абелева группа.
абелева группа.
43. Определение произведения рациональных чисел и его корректность. Поле рациональных чисел 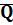
Определение: 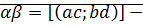 произведение рациональных чисел.
произведение рациональных чисел.
Теорема: определение произведения рациональных чисел корректно.
Доказательство: 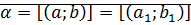
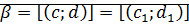
докажем: 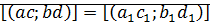
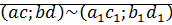
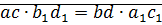
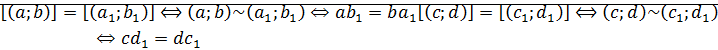
Перемножим равенства
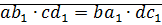
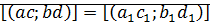 ⊠
⊠
Теорема: умножение рациональных чисел коммутативно, ассоциативно, дистрибутивно относительно сложения.
Доказательство: 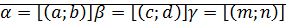
1) 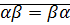 ?
?
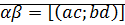
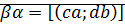
Умножение целых чисел коммутативно 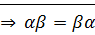
2) 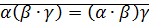
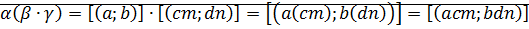
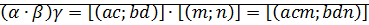
3) 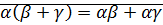
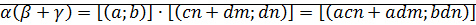
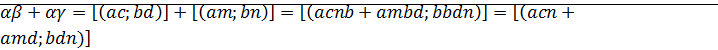 ⊠
⊠
Утверждение: рациональное число 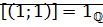 является нейтральным элементом относительно умножения в множестве Q.
является нейтральным элементом относительно умножения в множестве Q.
Утверждение: для любого рационального числа 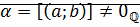 обратным является число
обратным является число 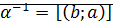
Следствие: 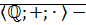 поле
поле
44. Отношение « 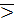 » в поле рациональных чисел и его корректность. Плотность множества рациональных чисел. Свойство трихотомии. Отношение “
» в поле рациональных чисел и его корректность. Плотность множества рациональных чисел. Свойство трихотомии. Отношение “ 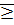 ” как отношение порядка в
” как отношение порядка в 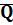
Утверждение. Произвольное рациональное число является классом пары, где 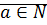 ,
, 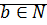 .
.
Доказательство: 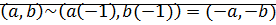 ⊠
⊠
Поэтому дальше будем использовать пары только с положительным вторым элементом.
Определение: Пусть 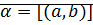 ,
, 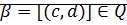 . Будем говорить
. Будем говорить 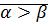 если
если 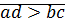 .
.
Теорема (корректность определения): Определение корректно.
Доказательство: 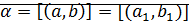 ,
, 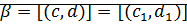
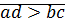 докажем:
докажем: 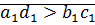
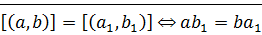
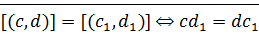
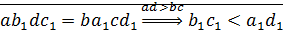 ⊠
⊠
Теорема: 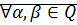 могут находиться только в одном соотношении:
могут находиться только в одном соотношении:
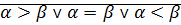
Доказательство:
Целые числа 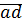 и
и 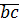 могут находиться только в одном из трех соотношений:
могут находиться только в одном из трех соотношений: 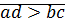 или
или 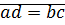 или
или 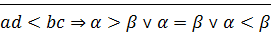 ⊠
⊠
Теорема: Отношение « 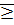 » является отношением порядка на
» является отношением порядка на 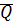 .
.
Доказательство:
· Рефлексивность 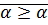
· Антисимметричность 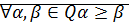 и
и 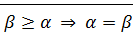
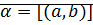
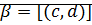
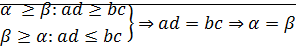
· Транзитивность: 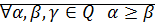 и
и 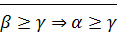
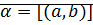
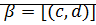
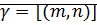
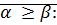
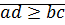 (1)
(1)
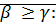
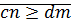 (2)
(2)
Докажем: 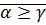
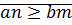
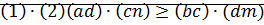
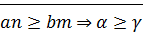 ⊠
⊠
Свойство (плотность множества рациональных чисел):
Множество рациональных чисел плотно, т. е. между произвольными неравными рациональными числами a и b существует по крайней мере одно рациональное число.
Док-во:
Пусть 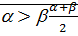 находится между ними
находится между ними
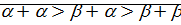
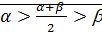 ⊠
⊠
