Ассоциативность умножения натуральных чисел.

Теорема (закон ассоциативности умножения)

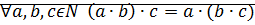
Доказательство:

ММИ (с) :

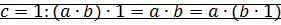
Пусть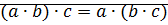

Докажем: ?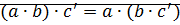

⊠

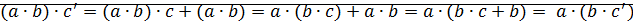14. Отношение «>» как отношение строгого порядка на множестве N. Свойство трихотомии: существование.

Определение 1:Пусть 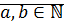. Будем говорить, что 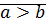, если 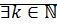, что

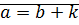
Свойство: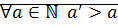

Доказательство: .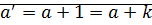

Теорема (Свойство трихотомии):

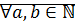имеет место только одно из соотношений: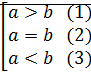

Доказательство (существование): 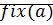, ММИ( ).

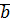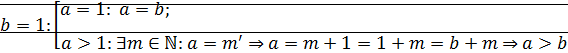
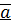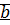Пусть для и выполняется одно из соотношений .

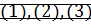Докажем для 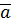и :

:

: ⊠

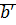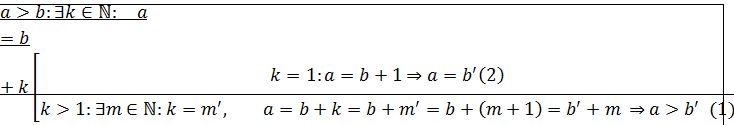
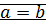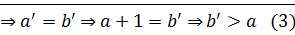
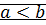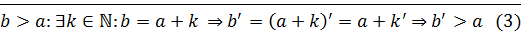Определение: Отношение 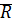на множестве 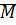называется отношением строгого порядка, если оно:

1) антирефлексивно: 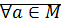: 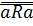истина.

2) ассиметрично: :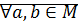

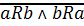
3) транзитивно: :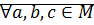

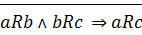
Теорема: Отношение 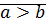является отношением строгого порядка на множестве .

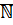15. Отношение «>» как отношение строгого порядка на множестве N. Свойство трихотомии: единственность.

Определение 1: Пусть 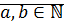. Будем говорить, что 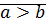, если 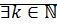, что

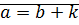
Свойство: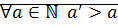

Доказательство: .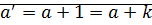

Теорема (Свойство трихотомии):

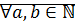имеет место только одно из соотношений: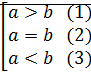

Доказательство (единственность): докажем, что никакие два соотношения 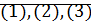одновременно не выполняются:

:

:

: , ⊠

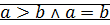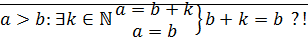
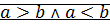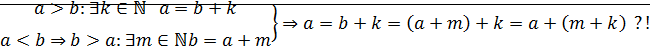
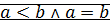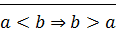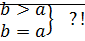Определение: Отношение 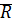на множестве 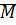называется отношением строгого порядка, если оно:

1) антирефлексивно: 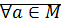: 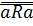истина.

2) ассиметрично: :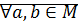

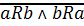
3) транзитивно: :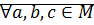

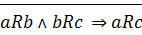
Теорема: Отношение 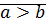является отношением строгого порядка на множестве .

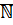16. Отношение « 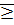» как отношение порядка на множестве N.

Определение: 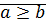, если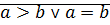

Определение: Отношение 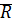на мн-ве 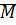называется отношением порядка, если оно:

1) рефлексивно: 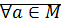: 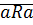истина.

2) антисимметрично: :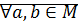

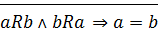
3) транзитивно: :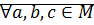

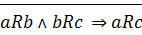
Теорема: Отношение « 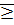» является отношением порядка на множестве .

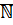Доказательство: 1), 2) – очевидно.

3) ?

,

,

⊠

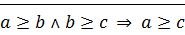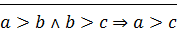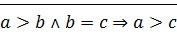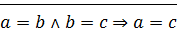17. Отношение « 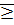» как отношение линейного порядка на множестве N

Определение : Отношение порядка 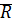на множестве 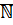называется линейным, если 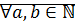выполняется: .

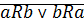Теорема: Отношение « 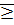» является отношением линейного порядка на множестве 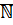, т.е.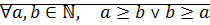

Доказательство: 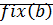, ММИ( )

:

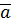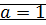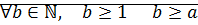
Пусть для 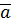выполняется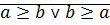

Докажем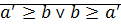

, ,

⊠

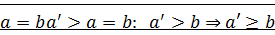
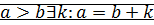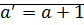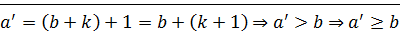
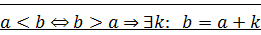
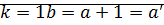
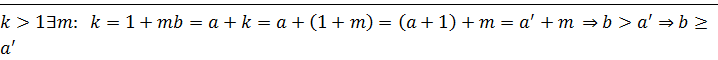Закон монотонности сложения на множестве N и следствия из него

Теорема (закон монотонности сложения):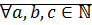

1)

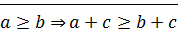
2)

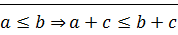
Доказательство: 1) ( )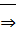

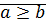
Если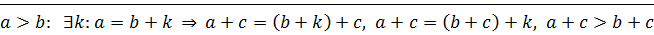

Если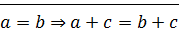

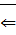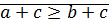( ) . От противного: пусть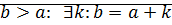

,

?!

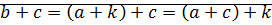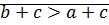2) Аналогично ⊠

Следствие: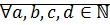

1)

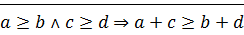
2)

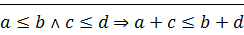
Закон монотонности умножения на множестве N и следствия из него

Теорема (закон монотонности умножения):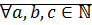

1)

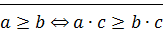
2)

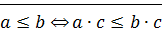
Следствие: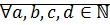

1)

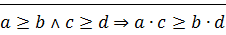
2)

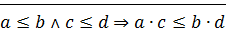
Дискретность и архимедовость множества натуральных чисел

Свойство (архимедовость множества )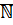

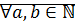
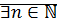
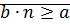
Доказательство: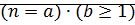

⊠

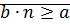Свойство (дискретность множества )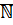

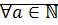
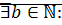
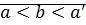
(Числа 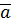и 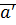– соседние. В дискретном множестве все точки изолированы, существует понятие «соседи»)

Доказательство: , ?! ⊠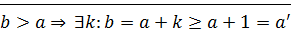

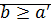Разность натуральных чисел: определение и единственность. Условие существования разности натуральных чисел

Определение: Натуральное число 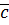(если оно существует) наз. разностью чисел 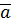и 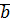, если .

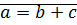Теорема

1)

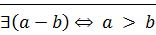
2) если разность существует, то она определена единственным образом.

Доказательство:

1)

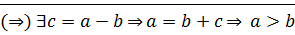
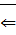( ) пусть ,

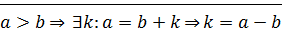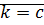
2)пусть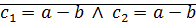

⊠
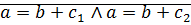
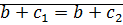
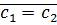