Множество натуральных чисел N. Аксиомы Пеано
Множество натуральных чисел N. Аксиомы Пеано
Определение: Множеством натуральных чисел называется непустое множество N, для элементов которого определено отношение «непосредственно следует за» (число которое непосредственно следует за 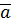 обозначается
обозначается 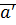 ), которое удовлетворяет следующим аксиомам:
), которое удовлетворяет следующим аксиомам:
1)  (существует натуральное число 1, которое непосредственно не следует ни за каким натуральным числом)
(существует натуральное число 1, которое непосредственно не следует ни за каким натуральным числом)
2)  (для каждого натурального числа
(для каждого натурального числа  единственное натуральное число
единственное натуральное число 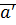 , которое непосредственно следует за ним)
, которое непосредственно следует за ним)
3)  (каждое натуральное число непосредственно следует не более чем за одним натуральным числом)
(каждое натуральное число непосредственно следует не более чем за одним натуральным числом)
4)  :
: 


Тогда  .
.
(множество M содержит все натуральные числа)
Аксиомы  называются аксиомами Пеано.
называются аксиомами Пеано.
Независимость аксиом Пеано
1)  (существует натуральное число 1, которое непосредственно не следует ни за каким натуральным числом)
(существует натуральное число 1, которое непосредственно не следует ни за каким натуральным числом)
2)  (для каждого натурального числа
(для каждого натурального числа  единственное натуральное число
единственное натуральное число 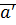 , которое непосредственно следует за ним)
, которое непосредственно следует за ним)
3)  (каждое натуральное число непосредственно следует не более чем за одним натуральным числом)
(каждое натуральное число непосредственно следует не более чем за одним натуральным числом)
4)  :
: 


Тогда  .
.
(множество M содержит все натуральные числа)
Аксиомы  называются аксиомами Пеано.
называются аксиомами Пеано.
1) Независимость 
 1 → 2
1 → 2
2) Независимость 
 3→5→….
3→5→….
1→2
4→6→….
3) Независимость 
 1→2→3
1→2→3
4) Независимость 
1→3→5→…..
2→4→6→….
Принцип полной математической индукции. Обобщенный принцип полной математической индукции. Примеры доказательства методом математической индукции
 :
:  . Тогда
. Тогда  (множество M содержит все натуральные числа)
(множество M содержит все натуральные числа)
Замечание: Из аксиомы  (аксиомы индукции) следует законность доказательств методом мат. индукции, при этом аксиома индукции применяется в следующем виде:
(аксиомы индукции) следует законность доказательств методом мат. индукции, при этом аксиома индукции применяется в следующем виде:
Теорема (принцип полной мат. индукции): Утверждение  ,
,  верно
верно  если выполняются след. условия:
если выполняются след. условия:
1)  – истина
– истина
2)  истина, то
истина, то  истина.
истина.
Доказательство:


 (условие 2)
(условие 2)
значит, по аксиоме индукции  . ⊠
. ⊠
Замечание: Доказательство на основании принципа полной математической индукции называется доказательство методом полной математической индукции. Говорят в этом случае коротко: докажем  индукцией по
индукцией по 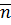 .
.
База индукции:  – истина ?
– истина ?
Предположение индукции: 
Шаг индукции:  (следует ли из
(следует ли из  T(
T(  ))
))
Пример: Доказать методом полной мат. индукции, что сумма 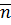 первых нечетных натуральных чисел равна
первых нечетных натуральных чисел равна 

1) T(1):  – истина.
– истина.



Сложение натуральных чисел как бинарная алгебраическая операция и как функция. Примеры. Свойство сокращения
Определение: Сложением на множественатуральных чисел называется бинарная алгебраическая операция
 (обознач (+), а результат называется суммой), которая удовл. следующим условиям:
(обознач (+), а результат называется суммой), которая удовл. следующим условиям:


Пример: Найти сумму 2+5





Определение: Сложением натуральных чисел называется функция  , причем выполняются условия:
, причем выполняются условия:


Теорема (свойство сокращения): 
Доказательство:  и
и 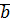 . ММИ по
. ММИ по 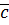 :
:
 :
: 
пусть  ,
,
докажем 
 ⊠
⊠
Закон монотонности умножения на множестве N и следствия из него
Теорема (закон монотонности умножения): 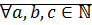
1) 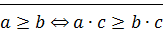
2) 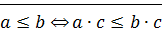
Следствие: 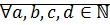
1) 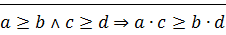
2) 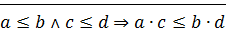
Поле действительных чисел.
Определение:Модулем действительного числа 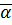 называется
называется
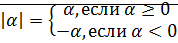
Определение: Пусть 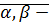 действителные числа, их произведением называется действительное число, которое определяется следующим образом:
действителные числа, их произведением называется действительное число, которое определяется следующим образом:
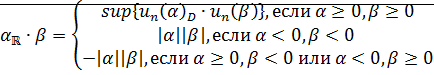
Теорема: Множество 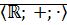 является кольцом. Умножение на
является кольцом. Умножение на 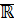 согласуется с умножением на
согласуется с умножением на 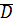 .
.
Доказательство:
1. для сложения всё уже доказано
2. Умножение – б. а. о.
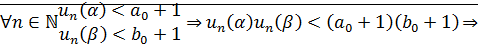
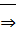 множество
множество 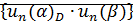 ограничено сверху
ограничено сверху 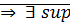 этого множества.
этого множества.
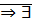 и единственным образом определено умножение неотрицательных действ-ых чисел.
и единственным образом определено умножение неотрицательных действ-ых чисел.
Следовательно, определено умножение действительных чисел.
3. ассоциативность: доказательство достаточно провести для неотрицательных чисел, потому что для других чисел это следует из этого случая:
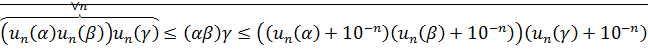 <
<
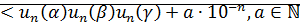
Аналогично:
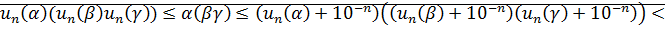
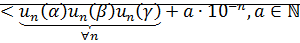
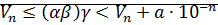
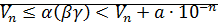
согласно следствию теоремы о плотности множества D в множестве 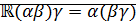
4. дистрибутивность 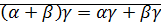 – это равенство очевидно, если одно из чисел
– это равенство очевидно, если одно из чисел 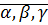 равно
равно 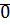 , или
, или 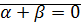 .
.
Достаточно доказать дистрибутивность для 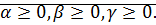 Доказательство аналогично доказательству для ассоциативности. ⊠
Доказательство аналогично доказательству для ассоциативности. ⊠
Теорема: 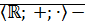 поле.
поле.
Доказательство: достаточно доказать, что если 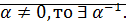
Будем считать, что 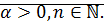 Тогда
Тогда 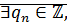 что
что 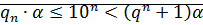
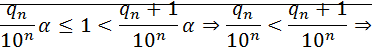
последовательность 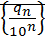 ограниченасверху
ограниченасверху 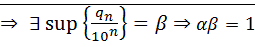 ⊠
⊠
Теорема: Множество действительных чисел содержит множество рациональных чисел. Отношение «=», отношение порядка, операции умножения и сложения на множестве 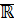 согласуются с соответствующими операциями на множестве
согласуются с соответствующими операциями на множестве 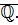
Доказательство: Множество 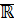 содержит множество
содержит множество 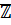 , поэтому мн-во
, поэтому мн-во 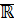 содержит мн-во чисел вида
содержит мн-во чисел вида 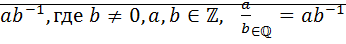 ⊠
⊠
Определение, свойства и алгебраические операции с комплексными числами. Действия над комплексными числами в алгебраической и тригонометрической формах. Вложение поля действительных чисел в поле комплексных чисел
Определение: Системой комплексных чисел называется множество 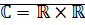 с операциями сложение и умножение:
с операциями сложение и умножение:
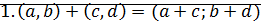 ;
; 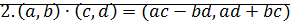 .
.
Теорема: Система комплексных чисел 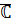 является полем.
является полем.
Доказательство:
1. Сложение коммут-но, ассоц-но, нулевой элемент 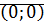 ; противоположный
; противоположный 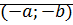 .
.
2. Умножение коммутативно, ассоциативно, единица 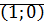 ;
;
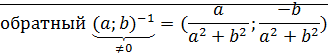
3. дистрибутивность ⊠
Обозначим 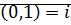 – называется комплексной единицей.
– называется комплексной единицей. 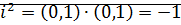 .
. 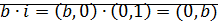 . Поэтому
. Поэтому 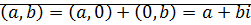 .
.
Определение: Комплексное число 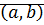 записанное в виде
записанное в виде 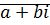 называется алгебраической формой комплексного числа.
называется алгебраической формой комплексного числа.
Утверждение: Сложение и умножение комплексных чисел в алгебраической форме:
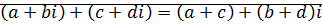 ;
;
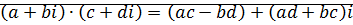 ;
;
Доказательство:
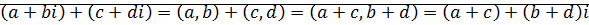 .
.
Аналогично для умножения. ⊠
Замечание: Рассмотрим пару 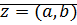 . Поставим в соответствие числа на декартовой плоскости с координатами
. Поставим в соответствие числа на декартовой плоскости с координатами 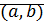 .
.
Длина вектора 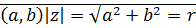
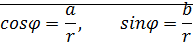
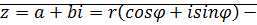 эта форма записи комплексного числа называется тригонометрической.
эта форма записи комплексного числа называется тригонометрической.
Утверждение:Умножение комплексных чисел в тригонометрической форме:
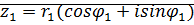 ;
; 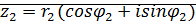 ,
,
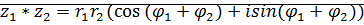 .
.
Утверждение: Если 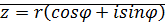 ,
, 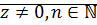 , то
, то 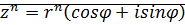 .
.
Определение: Корнем -ой степени из компл. числа 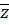 назыв. такое число
назыв. такое число 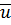 , что
, что 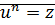 .
.
Обозначение: 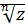 .
.
Теорема: Пусть 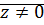 - комплексное число, тогда
- комплексное число, тогда 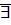 ровно
ровно 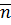 значений корня -ой степени из
значений корня -ой степени из 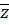 и они находятся по формуле:
и они находятся по формуле:
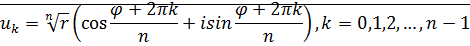
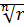 - арифметическое значение корня.
- арифметическое значение корня.
Следствие: Корни степени 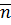 из
из 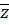 находятся в вершинах правильного -ка.
находятся в вершинах правильного -ка.
Следствие: Мн-во 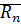 всех корней степени
всех корней степени 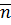 из 1 является мультипликативной группой.
из 1 является мультипликативной группой.
Доказательство:
· 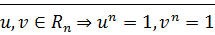
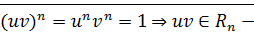 бинарная алгебраическая операция
бинарная алгебраическая операция
· 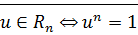
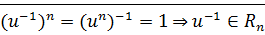
· 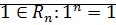 ⊠
⊠
Множество натуральных чисел N. Аксиомы Пеано
Определение: Множеством натуральных чисел называется непустое множество N, для элементов которого определено отношение «непосредственно следует за» (число которое непосредственно следует за 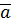 обозначается
обозначается 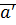 ), которое удовлетворяет следующим аксиомам:
), которое удовлетворяет следующим аксиомам:
1)  (существует натуральное число 1, которое непосредственно не следует ни за каким натуральным числом)
(существует натуральное число 1, которое непосредственно не следует ни за каким натуральным числом)
2)  (для каждого натурального числа
(для каждого натурального числа  единственное натуральное число
единственное натуральное число 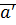 , которое непосредственно следует за ним)
, которое непосредственно следует за ним)
3)  (каждое натуральное число непосредственно следует не более чем за одним натуральным числом)
(каждое натуральное число непосредственно следует не более чем за одним натуральным числом)
4)  :
: 


Тогда  .
.
(множество M содержит все натуральные числа)
Аксиомы  называются аксиомами Пеано.
называются аксиомами Пеано.
Независимость аксиом Пеано
1)  (существует натуральное число 1, которое непосредственно не следует ни за каким натуральным числом)
(существует натуральное число 1, которое непосредственно не следует ни за каким натуральным числом)
2)  (для каждого натурального числа
(для каждого натурального числа  единственное натуральное число
единственное натуральное число 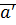 , которое непосредственно следует за ним)
, которое непосредственно следует за ним)
3)  (каждое натуральное число непосредственно следует не более чем за одним натуральным числом)
(каждое натуральное число непосредственно следует не более чем за одним натуральным числом)
4)  :
: 


Тогда  .
.
(множество M содержит все натуральные числа)
Аксиомы  называются аксиомами Пеано.
называются аксиомами Пеано.
1) Независимость 
 1 → 2
1 → 2
2) Независимость 
 3→5→….
3→5→….
1→2
4→6→….
3) Независимость 
 1→2→3
1→2→3
4) Независимость 
1→3→5→…..
2→4→6→….
Принцип полной математической индукции. Обобщенный принцип полной математической индукции. Примеры доказательства методом математической индукции
 :
:  . Тогда
. Тогда  (множество M содержит все натуральные числа)
(множество M содержит все натуральные числа)
Замечание: Из аксиомы  (аксиомы индукции) следует законность доказательств методом мат. индукции, при этом аксиома индукции применяется в следующем виде:
(аксиомы индукции) следует законность доказательств методом мат. индукции, при этом аксиома индукции применяется в следующем виде:
Теорема (принцип полной мат. индукции): Утверждение  ,
,  верно
верно  если выполняются след. условия:
если выполняются след. условия:
1)  – истина
– истина
2)  истина, то
истина, то  истина.
истина.
Доказательство:


 (условие 2)
(условие 2)
значит, по аксиоме индукции  . ⊠
. ⊠
Замечание: Доказательство на основании принципа полной математической индукции называется доказательство методом полной математической индукции. Говорят в этом случае коротко: докажем  индукцией по
индукцией по 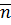 .
.
База индукции:  – истина ?
– истина ?
Предположение индукции: 
Шаг индукции:  (следует ли из
(следует ли из  T(
T(  ))
))
Пример: Доказать методом полной мат. индукции, что сумма 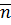 первых нечетных натуральных чисел равна
первых нечетных натуральных чисел равна 

1) T(1):  – истина.
– истина.



Сложение натуральных чисел как бинарная алгебраическая операция и как функция. Примеры. Свойство сокращения
Определение: Сложением на множественатуральных чисел называется бинарная алгебраическая операция
 (обознач (+), а результат называется суммой), которая удовл. следующим условиям:
(обознач (+), а результат называется суммой), которая удовл. следующим условиям:


Пример: Найти сумму 2+5





Определение: Сложением натуральных чисел называется функция  , причем выполняются условия:
, причем выполняются условия:


Теорема (свойство сокращения): 
Доказательство:  и
и 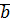 . ММИ по
. ММИ по 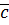 :
:
 :
: 
пусть  ,
,
докажем 
 ⊠
⊠
