Основные характеристики функционирования СМО с очередью.

Рассмотрим основные характеристики функционирования СМО с неограниченной длиной очереди. В таких системах поток заявок поступает извне. Примером подобной системы может служить любое предприятие сферы обслуживания (ателье, магазин, ресторан и т.д.). Эффективность функционирования таких систем определяется следующей совокупностью показателей:

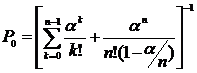-Вероятность того, что все обслуживающие каналы свободны:

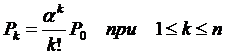-Вероятность того, что занято 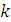каналов, при условии, что общее количество заявок не превышает числа каналов:

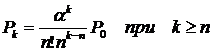-Вероятность того, что в системе находится 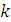заявок при условии, что число заявок больше числа каналов:

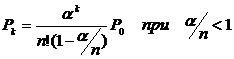-Вероятность того, что все каналы заняты:

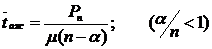-Среднее время ожидания в очереди:

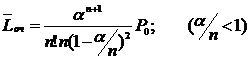-Средняя длина очереди:

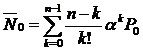-Среднее число свободных каналов:

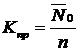-Коэффициент простоя каналов:

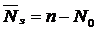-Среднее число занятых каналов:

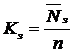- Коэффициент загрузки каналов:

Рассмотрим пример вычислений основных показателей эффективности функционирования СМО с неограниченной длиной очереди. Предположим, Фирма по ремонту радиоаппаратуры имеет 5 мастеров. В среднем в фирму поступает 10 заявок на ремонт в день. В среднем в день каждый мастер успевает отремонтировать 2,5 радиоаппарата. За единицу времени принимаем 7-часовой рабочий день.

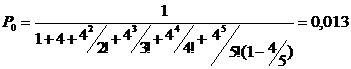На основании условия определяем: 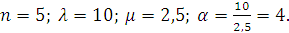Определим предельные вероятности состояний системы:

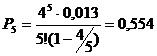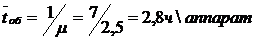Среднее время обслуживания одного аппарата:

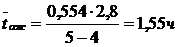Среднее время ожидания начала обслуживания:

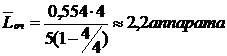Средняя длина очереди, от которой зависит площадь, необходимая для хранения принятых в ремонт аппаратов:

Среднее число мастеров, свободных от работы:

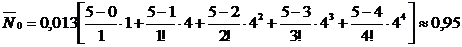В СМО с ограниченной длиной очереди поток заявок поступает изнутри системы. Например, в фирме имеется несколько единиц оборудования, которые случайным образом могут выходить из строя и требовать обслуживания в виде ремонта. Максимальное количество заявок на обслуживание в этом случае оказывается фиксированным. Оно обозначается .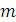

Эффективность функционирования таких систем характеризуют следующие показатели.

1. 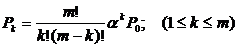Вероятность того, что занято 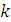каналов, при условии, что число заявок не больше числа каналов обслуживания:

2. 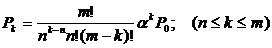Вероятность того, что в системе находится 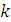заявок при условии, что число заявок больше числа каналов:

3. 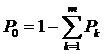Вероятность того, что все каналы свободны:

4. 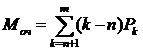Средняя длина очереди:

5. 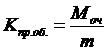Коэффициент простоя обслуживаемого объекта:

6. 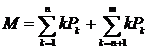Среднее число заявок:

7. 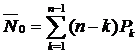Среднее число свободных каналов:

8. 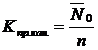Коэффициент простоя обслуживающего канала:

Рассмотрим пример задачи на расчет показателей эффективности функционирования СМО с ограниченной длиной очереди. Рабочий обслуживает группу из трех автоматов. В среднем автоматы требуют обслуживания с интенсивностью 2 авт.\час. На обслуживание одного автомата уходит в среднем 12 мин.

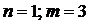
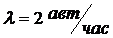
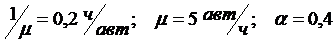На основании условий определяем:

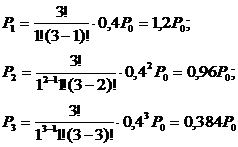Вероятности состояний определяем по формулам:

На основании расчетов заполним таблицу 36.

Таблица 36. Показатели эффективности функционирования СМО.

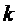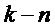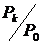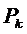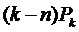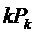		1,0000	0,2822
		1,2000	0,3386		0,3386
		0,9600	0,2709	0,2707	0,5418
		0,3840	0,1083	0,2166	0,3249
		3,5440	1,0000	0,4875	1,2053

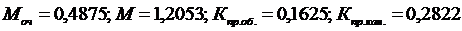Определим остальные показатели, используя расчеты, выполненные в таблице 36:

Заключение

В настоящем пособии отражены основные разделы традиционного курса исследования операций, содержание которых представляется автору наиболее важным и ценным с позиций требований, предъявляемых к профессиональной подготовке выпускников экономического факультета РГУ им. И. Канта.

В рамках реализации заявленной во введении цели были рассмотрены основные принципы разработки математических оптимизационных моделей, показаны подходы к их классификации. В соответствии с ранее выбранным принципом изложения в первых разделах пособия рассмотрены детерминированные модели, к числу которых относятся модели линейного и нелинейного (выпуклого) программирования, а также модели динамического программирования. В последующих разделах охарактеризованы вероятностные модели и модели с неопределенностью: математические игры, модели управления запасами и модели систем массового обслуживания.

В каждом разделе пособия автор стремился не только ознакомить читателей с математическим аппаратом, применяемым в моделировании, но и проиллюстрировать его применение на примерах экономических и управленческих ситуаций, требующих принятия решений. Остается надеяться, что такой подход позволил читателям увидеть и оценить возможности выбора оптимальных управленческих решений на основе методов математического программирования и исследования операций.

Задания для индивидуальной и самостоятельной работы.

Линейное программирование

Задание 1.1.

На предприятии имеется возможность выпускать n видов продукции П_j 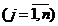. При ее изготовлении используются ресурсы, объемы запасов которых выражаются величинами 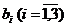. Нормы расходов ресурсов на выпуск одной единицы продукции П_j составляют а_ij. Цена единицы П_j равна с_j денежных единиц. Требуется:

1) симплексным методом найти план выпуска продукции по видам, который обеспечивал бы предприятию максимальный доход;

2) составить математическую модель двойственной задачи и дать ее содержательную экономическую трактовку;

3) найти компоненты оптимального плана двойственной задачи, используя данные заключительной симплексной таблицы исходной задачи;

4) определить целесообразность включения в план выпуска дополнительного вида продукции 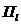, для которого даны нормы расхода ресурсов 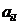и цена .

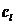Задание 1.2.

Смесь можно составить из n продуктов С_j 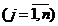. В каждом из продуктов содержится m компонентов. Минимально допустимый объем содержания i-го компонента в смеси выражается величиной 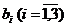. Содержание i-го компонента в единице j-го продукта выражается величиной а_ij. Цена единицы j-го продукта равна с_j. Составить смесь, минимальную по стоимости, используя для решения двойственную задачу.

Варианты контрольных заданий
Вариант
#1	1.2		C1	C2	C3	bi
		ci
		a1i
		a2i
		a3i
№2	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#3	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#4	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#5	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#6	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#7	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#8	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#9	1.1		П1	П2	П3	П4	П5	Пe	bi
		ci
		a1i
		a2i
		a3i
#10	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#11	1.1		П1	П2	П3	П4		Пe	bi
		ci	0,4	0,2	0,5	0,8
		a1i
		a2i
		a3i
#12	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#13	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#14	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#15	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#16	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#17	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#18	1.1		П1	П2	П3	П4	П5	Пe	bi
		ci
		a1i
		a2i
		a3i
#19	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i	1/6	3/7	1/4			5/9
		a2i	1/4	1/7	1/4			2/7
		a3i	1/6	1/7	3/8			2/7
#20	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i	1/2
		a3i	1/2	1/2
#21	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#22	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#23	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#24	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#25	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#26	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i	2,5	2,5		1,5
		a2i
		a3i
#27	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#28	1.2		C1	C2	C3	bi
		ci
		a1i
		a2i
		a3i
#29	1.2		C1	C2	C3	bi
		ci
		a1i
		a2i
		a3i
#30	1.2		C1	C2	C3	bi
		ci
		a1i
		a2i
		a3i
#31	1.2		C1	C2	C3	bi
		ci
		a1i
		a2i
		a3i
#32	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#33	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i
		a3i
#34	1.1		П1	П2	П3	П4		Пe	bi
		ci
		a1i
		a2i			2,5
		a3i
#35	1.2		C1	C2	C3	bi
		ci
		a1i
		a2i
		a3i
# 36	1.2		C1	C2	C3	bi
		ci
		a1i
		a2i
		a3i
#37	1.2		C1	C2	C3	bi
		ci
		a1i
		a2i
		a3i
						&nbs Наши рекомендации Свободные экономические зоны: определение, типология, основные характеристики функционирования. Основные операции с очередью Принципы функционирования и основные характеристики микрофонов Состав, назначение, основные характеристики и принципы функционирования системных и периферийных устройств ПК СМО с бесконечной очередью, первым обслуживающим прибором, с двумя приоритетами и бесконечной очередью для пуассоновских потоков. Граф, система уравнений Основные типы фирм. Экономические особенности функционирования фирм (предприятий) различных типов. Среда функционирования: внешняя и внутренняя Виды памяти: эмоциональная и двигательная память. Их характеристики и основные закономерности функционирования. Рынок: сущность и основные характеристики. Условия функционирования рынка. Модели рынка. Режимы функционирования государственной системы предупреждения и ликвидации чрезвычайных ситуаций. Основные мероприятия в различных режимах функционирования. Порядок функционирования и основные мероприятия при введении режимов функционирования государственной системы предупреждения и ликвидации чрезвычайных ситуаций. ← Предыдущая страница | Следующая страница →