Методы решения матричных игр.

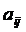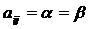Если в платежной матрице игры присутствует такой элемент , что , то говорят, что у игры есть седловая точка. В таком случае сам элемент 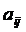называют ценой игры. Для обозначения цены игры введем особый символ 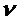(ню). Цена игры и пара альтернатив игроков, которая обеспечила данный исход игры, составляют решение игры.

В случае с седловой точкой решение игры находится в чистых стратегиях. Чистой стратегией игрока именуется такой способ поведения, когда одна из альтернатив выбирается с единичной вероятностью, а остальные альтернативы – с нулевой.

Как правило, в играх 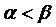, поэтому решение большинства игр находят в так называемых смешанных стратегиях. Смешанной стратегией игрока называют вектор, в котором каждая компонента соответствует вероятности (или частоте) выбора игроком соответствующей альтернативы. Ни одна компонента такого вектора не равна единице.

Обозначим смешанную стратегию игрока А 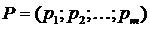, а смешанную стратегию игрока В 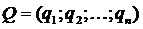. При использовании смешанных стратегий игра приобретает случайный характер, случайной величиной становится также и ее общий результат, который можно определить по формуле 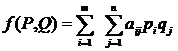. Функцию 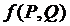называют платежной.

Смешанные стратеги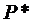и и 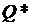являются оптимальными, если они образуют седловую точку для платежной функции игры. Это означает, что данные стратегии удовлетворяют неравенству

.

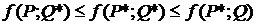Смысл данного неравенства таков: если А следует своей оптимальной смешанной стратегии, то независимо от стратегии В он получает выигрыш, не меньший чем цена игры; если В следует своей оптимальной смешанной стратегии, то независимо от стратегии А он получает проигрыш, не больший чем цена игры. Значение платежной функции от оптимальных смешанных стратегий является ценой игры

.

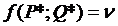Собственно решение начинается с упрощения платежной матрицы и изменения ее элементов. Упрощение состоит в исключении дублирующих (одинаковых по набору исходов) и доминируемых ( менее предпочитаемых с позиций удовлетворения интересов игрока) стратегий. Изменение элементов платежной матрицы состоит в том, чтобы сделать их целыми неотрицательными числами. В решении будем пользоваться упрощенной и видоизмененной матрицей. Решение осуществляется путем сведения игры к задаче линейного программирования на основе использования приведенного выше основного неравенства теории игр.

Воспользуемся левой частью этого неравенства, которую можно описать системой неравенств:

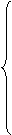
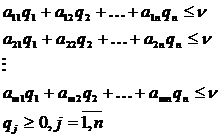
Для объяснения хода решения воспользуемся также матричной формой описания игры

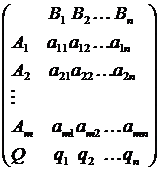
При этом 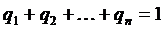, так как компонентами вектора являются вероятности полного набора возможных событий.

Разделим каждое неравенство системы и сумму компонентов вектора вероятностей на положительное число 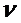. Поскольку элементы платежной матрицы можно сделать положительными числами, то можно сделать положительным и 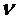. Введем обозначение 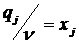. Так как игрок B стремится минимизировать исход 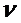, то он максимизирует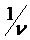

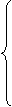
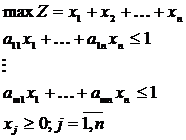
Решение данной задачи позволит получить 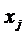, на основе которых вычисляются компоненты оптимального вектора 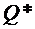и цена игры. На основе двойственных оценок получаем оптимальный вектор .

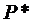Статистические игры.

Статистические игры образуют специальный класс матричных игр, в которых одним из участников является субъект, принимающий решение (игрок А – статистик), а другим – «природа» (игрок П). Под термином «природа» подразумевается весь комплекс внешних условий, в которых статистику приходится принимать решение. Статистик может осуществлять выбор решения из m возможных стратегий 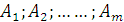. Природа может находиться в одном из n возможных состояниий .

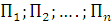Если статистик может численно оценить величиной 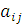последствия применения каждой своей стратегии 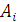при любом состоянии природы 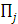, то игру можно задать платежной матрицей следующего вида:

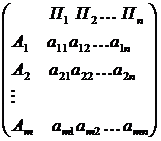
Содержание платежной матрицы определяется условием задачи. В частности, знак любого исхода зависит от того, каким образом данный исход удовлетворяет интересы игрока A. Любой позитивный ( с точки зрения интересов A ) исход выражается положительным числом, а негативный – отрицательным.

В играх с природой оптимальную стратегию игрока невозможно определить на базе основного неравенства теории игр, так как у природы нет осознанной стратегии, направленной против интересов A. Для определения оптимальной стратегии игрока А применяют некоторые критерии.

Начнем с рассмотрения ситуации с максимальной неопределенностью, когда о математических или статистических вероятностях наступления того или иного состояния природы ничего не известно. Для таких случаев предусмотрено применение критериев Вальда, Сэвиджа и Гурвица. Можно выделить два фактора, определяющих предпочтительный выбор того или иного критерия: 1) специфика условий, в которых приходится принимать решение; 2) субъективные склонности игрока А.

Критерий Вальда будет выбран наиболее осторожным игроком или же игроком, вынужденным принимать решение в крайне неблагоприятных условиях (ограниченность ресурсов, отсутствие резервов и невозможность позволить себе нести потери и т.д.). Ориентиром в выборе оптимального решения в таком случае будет максимин, уже известное нам число 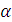, определяемое по платежной матрице как наибольшее среди наименьших по строкам матрицы чисел .

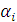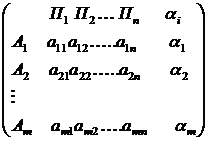
Игрок, более склонный к риску или имеющий резервы, для того чтобы рискнуть ради более ощутимого выигрыша, вероятнее всего остановит свой выбор на критерии Сэвиджа. Чтобы воспользоваться данным критерием, игроку придется рассчитать вспомогательные показатели 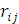, именуемые рисками. Для расчета рисков в платежной матрице выделяют наилучшие исходы по каждому состоянию природы ( максимальные числа в столбцах). Их обозначают .

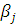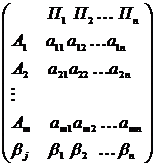
В каждом столбце риск определяется как отклонение фактического исхода от наилучшего при данном состоянии природы по формуле 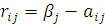. Затем в строках матрицы 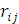выделяют максимальные риски, которые именуют 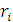. Оптимальной по критерию Сэвиджа будет альтернатива, соответствующая наименьшему среди .

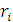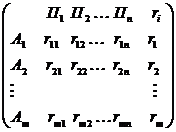
В ситуации максимальной неопределенности лицо, принимающее решение, может полагаться не только на логически структурированный выбор, но и на оценки частоты наступления наихудших и наилучших исходов, то есть на субъективное экспертное суждение. В таком случае выбор оптимальной альтернативы опирается на критерий Гурвица. Базовой основой данного критерия является параметр 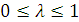, именуемый характеристикой «оптимизма-пессимизма», поскольку 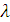соответствует частоте наступления наихудших исходов. Чем ближе 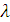к единице, тем более пессимистичен эксперт.

Технология выбора по критерию Гурвица такова. По строкам платежной матрицы выбираются наихудшие 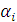и наилучшие 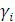исходы. Затем для каждой альтернативы вычисляются величины 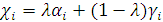. Оптимальной по критерию Гурвица является альтернатива с максимальным .

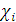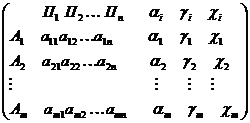
Выбор оптимальной альтернативы по критерию Лапласа опирается на максимальное математическое ожидание выигрыша игрока, рассчитанное с использованием равных вероятностей состояний природы. Делать выбор на основе критерия Лапласа вполне допустимо в ситуации с неизвестными вероятностями состояний ( при этом игрок исходит из допущения о равной вероятности наступления любого из состояний природы), но абсолютно правомерно его применение в тех случаях, когда состояния природы равновероятны, например, в силу того, что известна их математическая вероятность.

Технология выбора на основе критерия Лапласа основана на расчете ожидаемого выигрыша. Поскольку состояния равновероятны

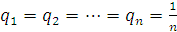, то математическое ожидание выигрыша рассчитывается по формуле 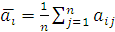. Максимальное математическое ожидание указывает на оптимальную альтернативу.

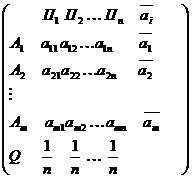
В ситуациях с известными вероятностями состояний природы используется критерий Байеса, который также базируется на расчете ожидаемого выигрыша. Для определения величины последнего вектор вероятностей состояний природы 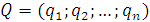необходимо умножить на вектор исходов в платежной матрице

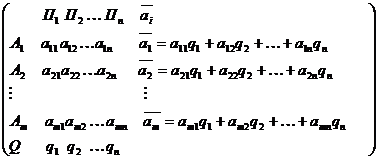
Оптимальна по критерию Байеса та альтернатива, у которой значение ожидаемого выигрыша 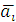максимально.

Рассмотрим применение разнообразных критериев выбора на примере.

Оборудование предприятия после нескольких лет эксплуатации может находиться в одном из следующих состояний: 1) требуется незначительный ремонт; 2) требуется частичная замена деталей; 3) требуется капитальный ремонт. Менеджмент предприятия определил следующие альтернативы выбора решения: 1) провести ремонт своими силами; 2) пригласить ремонтников со стороны; 3) заменить оборудование. Необходимо дать рекомендации относительно выбора оптимального решения для следующих ситуаций: а) вероятности состояний оборудования неизвестны; б) стали доступны статистические данные об опыте эксплуатации аналогичного оборудования, что позволило определить вероятность наступления каждого из его состояний.

Оценки затрат для каждого варианта решения приведены в таблице 26.

Таблица 26. Затраты, связанные с реализацией решений ( в ден. ед.).

Состояния   Альтернативы	1	2	3
1
2

Предположим, вероятности состояний оборудования неизвестны. Следовательно, мы можем опираться на критерии Вальда, Сэвиджа, Гурвица или, с известной долей условности, на критерий Лапласа.

Первым шагом к оптимальному выбору будет являться составление платежной матрицы. В нашем случае она формируется на основе данных таблицы 26. Необходимо определить лишь знаки исходов. Поскольку в условии задачи приведены данные о затратах, исходы платежной матрицы – отрицательные числа (табл. 27).

Таблица 27. Платежная матрица задачи.

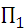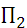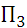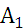	-2	-6	-10
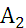	-10	-4	-8
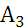	-14	-12	-6

Рассмотрим выбор на основе критерия Вальда ( табл. 28).

Таблица 28. Иллюстрация выбора на основе критерия Вальда.

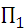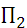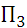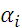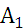	-2	-6	-10	-10
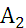	-10	-4	-8	-10
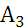	-14	-12	-6	-14

По критерию Вальда можно с одинаковым основанием выбрать либо первую, либо вторую альтернативу.

Теперь выберем оптимальную альтернативу по критерию Сэвиджа ( табл. 29 и 30). Сначала выберем наилучшие исходы по каждому из состояний.

Таблица 29. Выбор .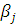

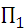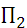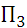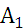	-2	-6	-10
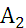	-10	-4	-8
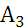	-14	-12	-6
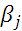	-2	-4	-6

Далее рассчитаем риски 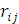и сделаем выбор.

Таблица 30. Иллюстрация выбора по критерию Сэвиджа.

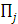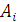	1	2	3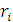
1
2

Критерий Сэвиджа предписывает остановить выбор на первой альтернативе.

Покажем применение критерия Лапласа (табл. 31). В данной задаче использование критерия Лапласа основано на допущении о равновероятности состояний оборудования. Вероятность каждого состояния в данном случае составляет

Таблица 31. Иллюстрация выбора по критерию Лапласа.

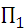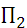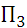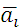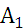	-2	-6	-10	-6
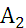	-10	-4	-8	-7,33
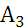	-14	-12	-6	-10,67

Критерий Лапласа указывает на первую альтернативу.

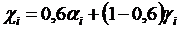И в завершение анализа ситуации с неизвестными вероятностями состояний покажем использование критерия Гурвица (табл. 32), предположив, что авторитетный эксперт оценил частоту наступления наихудших исходов на уровне 60%, то есть 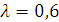. Основой выбора является вычисление величин

Таблица 32. Иллюстрация выбора по Гурвицу.

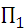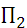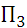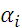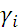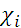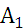	-2	-6	-10	-10	-2	-6,8
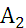	-10	-4	-8	-10	-4	-7,6
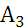	-14	-12	-6	-14	-6	-10,8

По критерию Гурвица оптимальна первая альтернатива.

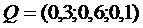Перейдем к анализу ситуации «б». Предположим, стали доступны данные об опыте эксплуатации аналогичного оборудования, из которых следует, что в 30% наблюдаемых случаев наступало первое состояние, в 60% - второе и лишь в 10% - третье. Следовательно, вектор вероятностей

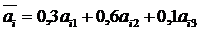Для вычисления ожидаемых выигрышей воспользуемся формулой

Выбор по критерию Байеса показан в таблице 33.

Таблица 33. Иллюстрация выбора по критерию Байеса.

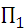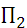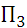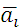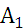	-2	-6	-10	-5,2
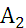	-10	-4	-8	-6,2
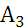	-14	-12	-6	-12

На основе критерия Байеса рекомендуется выбрать первую альтернативу.

Особенность данной задачи в том, что выбор по всем критериям совпадает. Однако часто разные критерии указывают на разные альтернативы, и к этому следует относиться как к естественному явлению. В таких случаях игрок должен определиться с предпочтениями и ориентировать выбор оптимальной альтернативы по самому важному и значимому для него критерию.