Вопрос 16. Решение систем методом Крамера

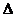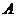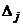Теорема Крамера. Пусть - определитель матрицы системы , а - определитель матрицы, получаемой из матрицы 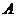заменой 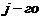столбца столбцом свободных членов. Тогда, если 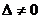, то система имеет единственное решение, определяемое по формулам: ( ).

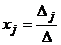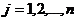Пример. Решить систему уравнений .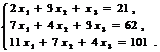

Вычислим определители: , , , .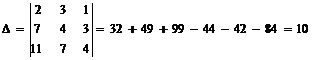

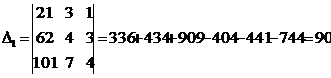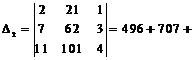
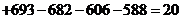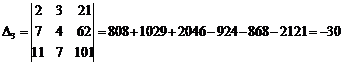Итак, , , .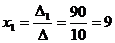

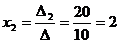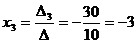Решение систем матричным методом.

Этот способ или, как его еще называеют, метод обратной матрицы называется так потому, что все решение сводится к простому матричному уравнению, для решения которого необходимо найти обратную матрицу. Для того, что бы расставить все точки над и, рассмотрим метод под микроскопом.

Алгоритм решения достаточно просто. Как и в методах Гаусса и Крамера первоначально надо проверить, имеет ли система уравнений решение по теореме Кронекера-Копелли. Затем для решения матричным методом необходимо ввести в рассмотрение матрицы-столбцы для неизвестных X и свободных членов B. Тогда систему линейных уравнений можно записать в матричной форме AX=B. Умножив это матричное уравнение на A^-1, получим A^-1AX= A^-1B, откуда EX=X=A^-1B. Следовательно, матрица-решение X легко находится как произведение A^-1 и B.

Для большей ясности решим небольшой пример методом обратной матрицы:

21x₁-45x₂-3.5x₃=10

12x₁-16x₂+21x₃=-16

14x₁+13x₂-8x₃=10

Определим совместность системы уравнений. По теореме Кронекера-Копелли для того, что бы система линейных алгебраических уравнений была совместна (имела решение), необходимо и достаточно, что быранг основной матрицы

A=	-45 3.5 -16 -8

и ранг расширенной матрицы

B=	-45 3.5 -16 -19 -8

были равны.
Так как rang|A|=3 равен rang|B|=3 и равен количеству неизвестных n=3, то система имеет единственное решение.

Для решения методом обратной матрицы необходимо ввести матричные обозначения

A=

-45 3.5 -16 -8

X=

X1 X2 X3

C=

-19

, то X=A-1C

Найдем обратную матрицу A^-1. Как ее найти, показывать не будем. Воспользовавшись нашии онлайн калькулятором, вы сможете выбрать один из двух способов для ее нахождения. Она будет иметь вид.

A-1=	0.008 0.016 0.046 -0.02 0.011 0.021 -0.02 0.047 -0.011

Для нахождения матрицы X умножим обратную матрицу А^-1 на матрицу С

0.008 0.016 0.046 -0.02 0.011 0.021 -0.02 0.047 -0.011

-19

=

0.227 -0.209 -1.194

Получили решение системы уравнений

X₁=0.227
X₂=-0.209
X₃=-1.194

ВОПРОС 18. Теорема Кронекера-Капелли. Решение систем линейных алгебраических уравнений в соответствии с теоремой Кронекера-Капелли.

Необходимость

Пусть система совместна. Тогда существуют числа 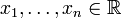такие, что 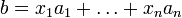. Следовательно, столбец 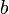является линейной комбинацией столбцов 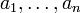матрицы 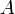. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

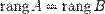Достаточность

Пусть 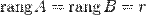. Возьмем в матрице 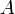какой-нибудь базисный минор. Так как 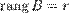, то он же и будет базисным минором и матрицы 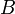. Тогда согласно теореме о базисном миноре последний столбец матрицы 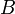будет линейной комбинацией базисных столбцов, то есть столбцов матрицы 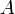. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы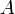

Следствия

Количество главных переменных системы равно рангу системы.

Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

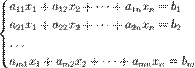(1)

Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.

Здесь 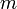— количество уравнений, а 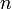— количество неизвестных. x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными^[1]. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[2].

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾, …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

ВОПРОС 21. Прямая на плоскости и в пространстве.. Взаимосвязь различных видов уравнений прямой.

Рассмотрим различные виды уравнений прямой на плоскости.

Пусть прямая проходит через точку М₀ (x₀,y₀) перпендикулярно вектору n = {A,B}. Тогда вектор , где М(х,у) — произвольная точка прямой, ортогонален n. Поэтому координаты любой точки данной прямой удовлетворяют уравнению

А(х — х₀) + В(у — у₀) = 0 - (7.3)

уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Замечание. Вектор n называется нормалью к прямой.

Преобразуем уравнение (7.3) к виду:

Ах + Ву + (-Ах₀ — Ву₀) = 0.

Обозначив -Ах₀ — Ву₀ = С, получим общее уравнение прямой:

Ах + Ву + С = 0. (7.4)

Получим теперь уравнение прямой, проходящей через точку М₀ (x₀,y₀) параллельно вектору q = {l,m}. Так как вектор , где М(х,у) — произвольная точка прямой, коллинеарен q, координаты любой точки данной прямой удовлетворяют уравнению

, (7.5)

называемому каноническим уравнением прямой. Вектор q при этом называется направляющим вектором прямой. В частности, если прямая проходит через точки М₁(х₁,у₁) и М₂(х₂,у₂), ее направляющим вектором можно считать , и из уравнения (7.5) следует:

- (7.6)

параметрические уравнения прямой.

Для прямой l, не параллельной оси Оу, можно ввести так называемый угловой коэффициент k — тангенс угла, образованного прямой и осью Ох, и записать уравнение

у l прямой в виде:

у = kx + b - (7.8)