Основные причины наличия в регрессионной модели случайного отклонения.

Основные причины наличия в регрессионной модели случайного отклонения.

Невключение в модель всех объясняющих переменных.

Проблема в том, что никогда заранее не известно, какие факторы при создав­шихся условиях действительно являются определяющими, а какими можно пренебречь. Здесь уместно отметить, что в ряде случаев учесть непосредственно какой-то фактор нельзя в силу невозможности получения по нему статистических данных.

Неправильный выбор функциональной формы модели.

Из-за слабой изученности исследуемого процесса либо из-за его переменчивости может быть неверно подобрана функция, его моделирующая. Это, безусловно, скажется на отклонении моде­ли от реальности, что отразится на величине случайного члена.

Агрегирование переменных.

Во многих моделях рассмат­риваются зависимости между факторами, которые сами пред­ставляют сложную комбинацию других, более простых пере­менных.

Ошибки измерений.

Какой бы качественной ни была мо­дель, ошибки измерений переменных отразятся на несоответствии модельных значений эмпирическим данным, что также отразится на величине случайного члена.

Ограниченность статистических данных.

Зачастую строятся модели, выражаемые непрерывными функциями. Но для этого используется набор данных, имеющих дискретную структуру. Это несоответствие находит свое выражение в слу­чайном отклонении.

Непредсказуемость человеческого фактора.

Эта причи­на может «испортить» самую качественную модель. Действи­тельно, при правильном выборе формы модели, скрупулезном подборе объясняющих переменных все равно невозможно спрогнозировать поведение каждого индивидуума.

Основные этапы регрессионного анализа.

1) выбор формулы уравнения регрессии;

2) определение параметров выбранного уравнения;

3) анализ качества уравнения и проверка адекватности урав­нения эмпирическим данным, совершенствование уравнения.

Определение теоретической линейной регрессионной модели.

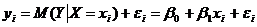(4.6)

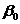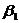Соотношение (4.6) называется теоретической линейной регрессионной моделью; и — теоретическими парамет­рами (теоретическими коэффициентами) регрессии; 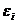— слу­чайным отклонением, зависимая переменная У и одна объ­ясняющая переменная X ( 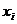— значения независимой перемен­ной в 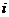-м наблюдении, .

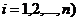Суть метода наименьших квадратов (МНК).

его суть состоит в минимизации суммы квадратов отклонений наблю­даемых значений зависимой переменной У от ее значений У, получаемых по уравнению регрессии.

Формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК.

Пусть по выборке 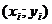, i = 1, 2, ... , n, требуется определить оценк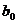и и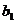

эмпирического уравнения регрессии (4.8). В этом случае при использовании МНК минимизируется следующая функция (рис.4.4)

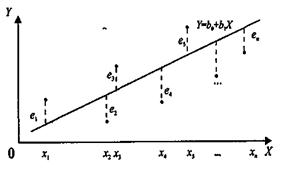
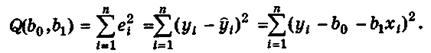
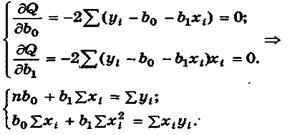
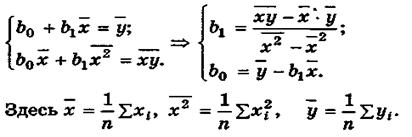
Предпосылки МНК

1°. Математическое ожидание случайного отклонения 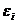равно нулю для всех наблюдений:

M( 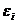) = 0, i = 1, 2, ..., п.

2°.Гомоскедастичностъ (постоянство дисперсии откло­нений). Дисперсия случайных отклонений 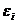< постоянна:

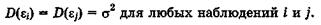
3°. Отсутствие автокорреляции.

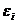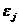Случайные отклонения и - являются независимыми друг от друга для всех

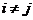
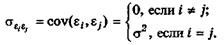
4°. Случайное отклонение должно быть независимо от объясняющих переменных.

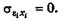
5°. Модель является линейной относительно параметров. .Для случая ножественной линейной регрессии сущест­венными являются еще две предпосылки.

6°. Отсутствие мультиколлинеарности.

Между объясняющими переменными отсутствует строгая (сильная) линейная зависимость.

7°. Ошибки 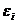, i= 1, 2, ..., n, имеют нормальное распределе­ние ( .

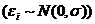Выполнимость данной предпосылки важна для проверки статистических гипотез и построения интервальных оценок.

При невыполнимости данной предпосылки (при гетероске­дастичности) последствия применения МНК будут следующи­ми.

Оценки коэффициентов по-прежнему останутся несме­щенными и линейными.

1. Оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками дан­ного параметра). Они не будут даже асимптотически эффектив­ными. Увеличение дисперсии оценок снижает вероятность по­лучения максимально точных оценок.

2. Дисперсии оценок будут рассчитываться со смещением. Смещенность появляется вследствие того, что не объясненная

уравнением регрессии дисперсия 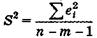(т - число объ ясняющих переменных), которая используется при вычисле­нии оценок дисперсий всех коэффициентов (формула (6.23)), не является более несмещенной.

4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно,статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным за­ иключениям по построенной модели. Вполне вероятно, что стан­дартные ошибки коэффициентов будут занижены, а следова­тельно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковы­ми на самом деле не являющихся.

1. 13)Характеристика коэффициентов уравнения регрессии. С помощью т статистики, Р, грубое правило

Примеры использования логарифмических регрессионных моделей.

Примеры использования обратных и степенных моделей.

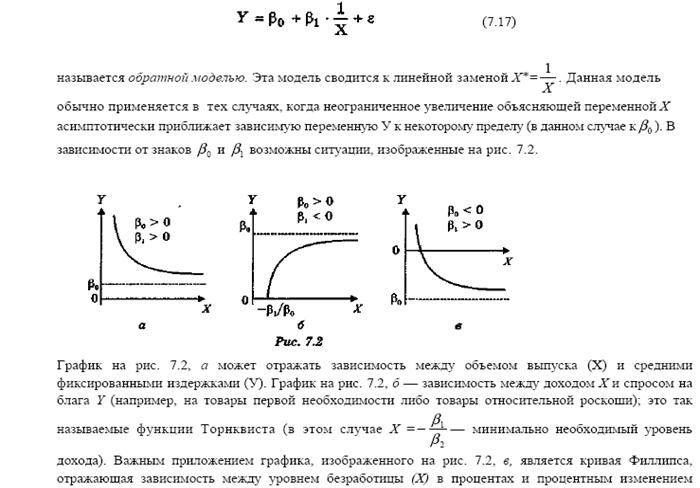заработной платы. При этом точка пересечения кривой с осью ОХ определяет естественный уровеньбезработицы.

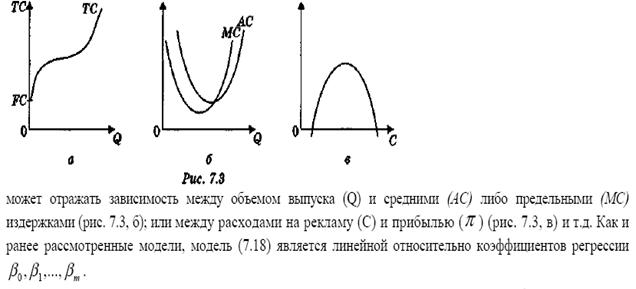
Примеры использования показательных функций в регрессионных моделях.

С С

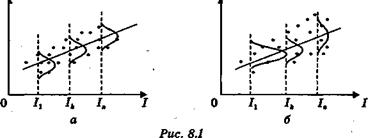
Динамика изменения дисперсий (распределений) отклонений для данного примера проил­люстрирована на рис. 8.2. При гомоскедастичности (рис. 8.2, а) дисперсии 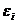постоянны, а при гетероскедастичности (рис. 8.2, б) дисперсии 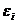изменяются (в нашем примере увеличиваются).

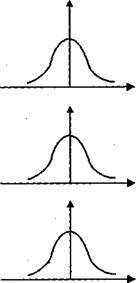Рис 8.2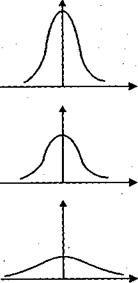

Проблема гетероскедастичности характерна для перекрест­ных данных и довольно редко встречается при рассмотрении временных рядов.

Последствия: При невыполнимости данной предпосылки (при гетероске­дастичности) последствия применения МНК будут следующи­ми.

Оценки коэффициентов по-прежнему останутся несме­щенными и линейными.

3. Оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками дан­ного параметра). Они не будут даже асимптотически эффектив­ными. Увеличение дисперсии оценок снижает вероятность по­лучения максимально точных оценок.

4. Дисперсии оценок будут рассчитываться со смещением. Смещенность появляется вследствие того, что не объясненная

уравнением регрессии дисперсия 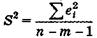(т - число объ ясняющих переменных), которая используется при вычисле­нии оценок дисперсий всех коэффициентов (формула (6.23)), не является более несмещенной.

4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным за­ иключениям по построенной модели. Вполне вероятно, что стан­дартные ошибки коэффициентов будут занижены, а следова­тельно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковы­ми на самом деле не являющихся.

Обнаружение:а) Графический анализ остатков

б) Тест ранговой корреляции Спирмена

в) Тест Парка

г) Тест Глейзера

д) Тест Голдфелда—Квандта

Спецификация модели

Одним из базовых предположений построения качествен­ной модели является правильная (хорошая) спецификация урав­нения регрессии. Правильная спецификация уравнения регрес­сии означает, что оно в целом верно отражает соотношение ме­жду экономическими показателями, участвующими в модели. Это является необходимой предпосылкой дальнейшего качест­венного оценивания.

Неправильный выбор функциональной формы или набора объясняющих переменных называется ошибками специфика­ции.

T-статистики

Дарбина—Уотсона dw

Проблемы спецификации

Однако необходимо предостеречь от абсолютизации полу­ченного результата, поскольку даже качественная модель явля­ется подгонкой спецификации модели под имеющийся набор данных. Поэтому вполне реальна картина, когда исследовате­ли обладающие разными наборами данных, строят разные мо­дели для объяснения одной и той же переменной. Проблематич­ным является и использование модели для прогнозирования значений объясняемой переменной. Иногда хорошие с точки зрения диагностических тестов модели обладают весьма низки­ми прогнозными качествами.

Одно из главных направлений эконометрического анали­за — постоянное совершенствование моделей. Здесь следует от­метить, что какого-то глобального подхода, определяющего за­ранее возможные пути совершенствования, нет и, скорее всего, быть не может. Исследователь должен помнить, что совершен­ной модели не существует. В силу постоянно изменяющихся ус­ловий протекания экономических процессов не может быть и постоянно качественных моделей. Новые условия требуют пе­ресмотра даже весьма устойчивых моделей.

Основные причины наличия в регрессионной модели случайного отклонения.