Приложения определенного интеграла: вычисление площади плоской фигуры.

Вычисление площадей.

а) 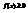и непрерывна, тогда площадь криволинейной трапеции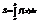

б) x=a, x=b и y=f(x), y=g(x); 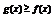на [a,b]

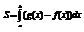
Замечание :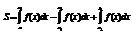

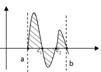
в) Пусть кривая задана параметрическим уравнением.

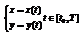
В данном случае мы не знаем явного задания кривой, поэтому при вычислении площади делаем замену, что бы свести к известным формулам.

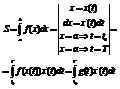
x(t)-убывает

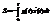
Пример(Вычислить площадь фигуры)

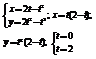
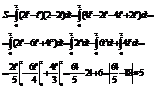
Вычисление площади в полярной системе координат.

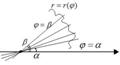Если линия, ограничивающая фигуру, задана в полярной системе координат, то в качестве основной фигуры принимает криволинейный сектор, то есть фигуру ограниченную 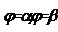и графиком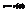

Разобьем 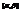(а вместе с ним и весь сектор)на частичные сектора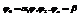

Каждый частичный сектор заменим круговым сектором. То есть будем считать, что на каждом из частичных промежутков 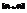функция 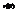изменится мало и приблизительно равна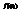

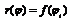
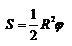
Приложения определенного интеграла: вычисление объемов

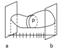
а) Вычисление объема тела по площадям поперечного сечения.

Рассмотрим тело(V), заключенное между плоскостями x=a, x=b.

Разобьем промежуток [a,b] на частичные промежутки, то есть тело разобьется на слои, параллельные плоскостям x=a, x=b.

Возьмем произвольную 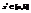и через 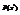, обозначим площадь сечения тела V плоскостью 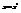. Сделаем следующие предположения:

1) При проецировании любых двух сечений друг на друга вдоль оси x, хотя бы одно из них проецируется на другое (внутрь другого).

2) Все сечения имеют в качестве площади непрерывную функцию f(x). Тогда объем слоя соответствует выделенному сечению, будет равен 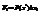. Где 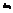- толщина слоя. Что бы получить объем всего тела, суммируем по слоям и перейдем к пределам.

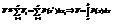
б) Пусть 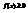на [a,b], непрерывна на замкнутой прямой. Вращением кривой y=f(x) получим, некоторое тело.

Полученное тело вращения будет подходить по рассматриваемый в a) случай. Т.к. сечение этого тела проецируется на перпендикулярную плоскость в виде кругов. Разбиваем [a,b] на частичные промежутки в каждом из которых, выбираем точку 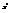. Сечения этого тела плоскостями 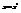будут представлять собой круги радиуса 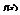. Поэтому 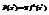суммируются по всем частям промежутка и переходя к пределу получаем, что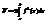

Приложения определенного интеграла: вычисление длины дуги

а) Пусть y=f(x)-непрерывная функция имеющая непрерывную производную и заданная на [a,b] .

Определение : Длиной дуги кривой назовем предел, к которому стремится вписанной к нему ломаной при неограниченном увеличении числа ее сторон и при стремлении наибольшей из ее сторон к 0.

Разобьем [a,b] на n-частей, где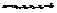

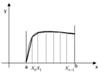
Проведем через две последующие точки деления дуги хорды. Построим ломаную.

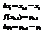
Длина ломаной 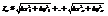Или, вынося 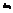за знак корня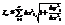

С учетом формулы конечного приращения Лагранжа, согласно которой имеем , .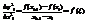

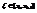Формулу длины выражает интеграл суммы 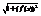. Поэтому вся длина дуги вычисляется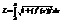

Дифференциальные уравнения. Основные понятия

Основные понятия определения.Дифференциальное уравнение называется соотношение вида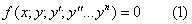 связывающее независимую переменную х, ее ф-цию у, а также производные этойфункции до н-го порядка включительно. если в уравнении 1 входит однанезависимая переменная, то такое диф. ур. называется обыкновенным, если вуравнение 1 входит несколько независимых переменных, то такое диф. ур.называется уравнение в частных производных. Порядком дифференциальногоуравнения называется порядок старшей производной, входящей в это уравнение.Решением уравнения 1 называется н-раз дифференцированная функция y=f(x),которая при подстановке в уравнение 1 обращает его в тождество. В простейшемслучае определение функции y=f(x) сводится к вычислению интеграла, а поэтомупроцесс нахождения решения диф. уравн. называется его интегрированием, аграфик ф-ции y=f(x) называется интегральной кривой диф. уравн. Т.к. приинтегрировании функции получается множество решений, отличающихся друг отдруга постоянным коэффициентом, то любое диф. уравн. также будет иметьмножество решений, графически определяемых семейством интегральных кривых.Общим решением (общим интегралом) диф. уравн. н-го порядка называется егорешение явно (неявно) выраженное относительно ф-ции у и содержащей н-независимых производных постоянных. 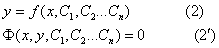Независимость констант С_I означает, что ни одна из них не может бытьвыражена через остальные, а следовательно число этих констант не может бытьуменьшено на единицу.Частным решением интеграла диф. уравн. н-го понрядка называется такое егорешение, в котором произвольным константам С_i присвоены конкретныезначения. это конкретные значения находятся из решения системы так называемыхначальных условий 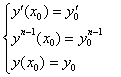В этой системе правые части равенства представляют собой некоторые константы. 9.Дифференциальные уравнения с разделяющимися переменными