Сопротивление в цепи синусоидального тока. Комплексная форма расчета.

=

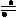
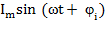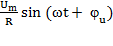
Каждой синусоидальной функции ставим в соответствие ее комплексное изображение:

;

;

;

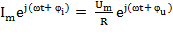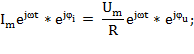
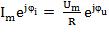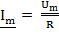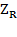– комплексное сопротивление резистора,

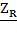= R, тогда закон Ома на резисторе в комплексной форме имеет вид:

,

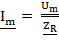аналогичное выражение справедливо и для действующих значений:

.

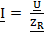Индуктивность в цепи синусоидального тока. Тригонометрическая форма расчета.

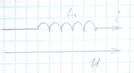
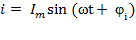, L = const, U - ?

Найдем напряжение в виде , .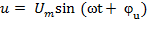

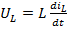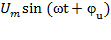=L

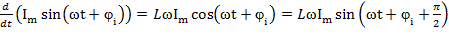
Тригонометрическая форма расчета.

А)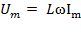

Обозначим 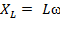– реактивное сопротивление индуктивности [Ом]

Закон Ома:

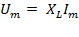– для амплитудных значений,

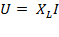– для действующих значений.

Закон Ома на индуктивности выполняется для амплитудных и действующих значений, но не выполняется для мгновенных значений, так как у напряжения и тока разная фаза.

Б) ;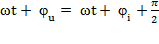

;

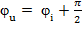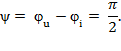
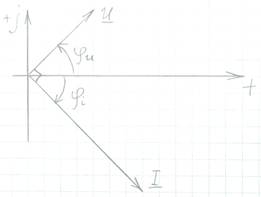
То есть начальная фаза напряжения на 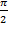больше начальной фазы тока. Другими словами, напряжение на индуктивности опережает ток на 90 градусов.

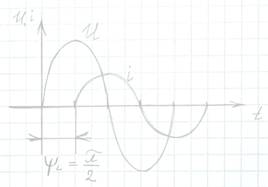
Индуктивность в цепи синусоидального тока. Комплексная форма расчета.

=

.

;

.

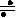
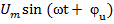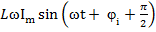
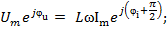
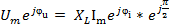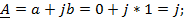
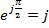
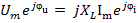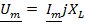Обозначим 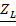= 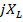– комплексное сопротивление индуктивности.

Тогда закон Ома на индуктивности в комплексной форме имеет вид:

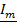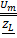= – для амплитудных значений;

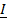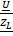= – для действующих значений.

Емкость в цепи синусоидального тока. Тригонометрическая форма расчета.

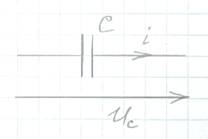Переменный ток в емкости.

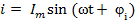, С = const, U_c - ?

= ;

= .

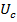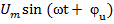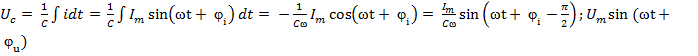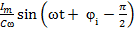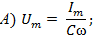
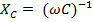– реактивное сопротивление емкости [Ом]

Тогда закон Ома на емкости для амплитуд примет вид:

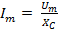– для амплитудных значений;

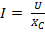– для действующих значений.

Б) = ;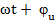

=

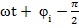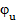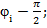
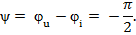
То есть разность фаз между напряжением и током на емкости = -90 градусов. Другими словами, ток опережает напряжение на 90 градусов, или напряжение на емкости отстает от тока на 90 градусов.

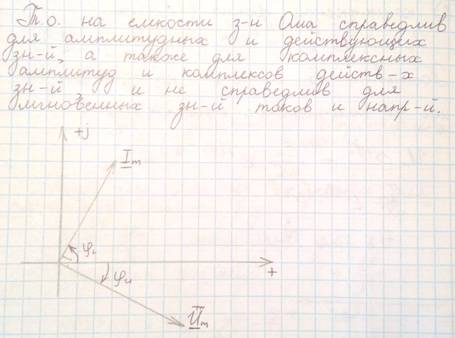
21. Емкость в цепи синусоидального тока. Комплексная форма расчета.

22.

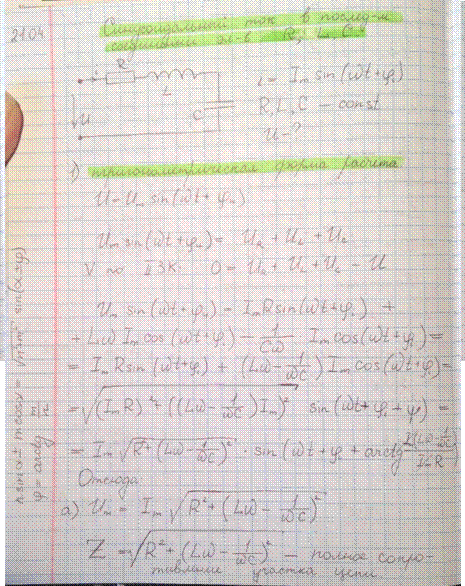Синусоидальный ток в цепях с последовательным соединением элементов R,L,C. Тригонометрическая форма расчета.

1. Синусоидальный ток в цепях с последовательным соединением элементов R,L,C. Комплексная форма расчета.

24.

Синусоидальный ток в цепях с параллельным соединением элементов R,L,C. Тригонометрическая форма расчета.

1. Синусоидальный ток в цепях с параллельным соединением элементов R,L,C. Комплексная форма расчета.

1. Представление синусоидальной функции комплексным числом.

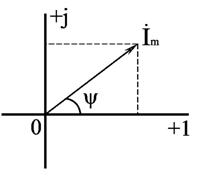
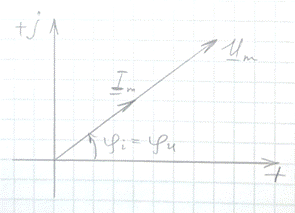
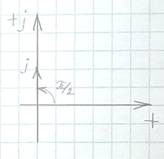
Рис. 1

Синусоидальный ток i(t) = I_m sin(ωt + ψ) можно представить комплексным числом Í_m на комплексной плоскости (рис. 1)

Í_m = I_me^jψ,

где амплитуда тока I_m – модуль, а угол ψ, являющийся начальной фазой, – аргумент комплексного тока.

Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока.

27. Комплексная форма записи законов Кирхгофа.