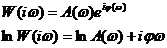Типовые входные сигналы (импульсная функция)

Единичная импульсная функция (дельта функция)

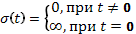
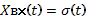
Основное свойство дельта функции, заключается в том, что она имеет единичную площадь, тоесть

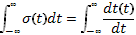^=1.

11.Типовые входные сигналы (гармоническая ф-я времени).

Гармоническое воздействие — сигнал синусоидальной формы, описываемый функцией

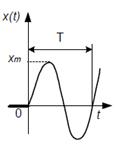
x(t)=x_msinωt, (-∞<t<∞), где х_т - амплитуда сигнала; ω= 2л/Т— круговая частота; Т- период сигнала. Гармонический сигнал, начинающий действовать в момент времени t = 0, описывают при помощи единичной ступенчатой функции:

x(t) = 1(t)x_msinωt, (0≤t<∞).

У НАС В ЛЕКЦИЯХ Xm ОБОЗНАЧАЛИ КАК А (типа амплитуда)

12 Временные характеристики.

Временные характеристики показывают закон изменения во времени регулируемой величины при изменении внешнего воздействия по определенному закону и при нулевыз начальныз условиях. В.Х. отражают динамические cd-df САУ, КОТОРЫЕ М,Б, ОПРЕДЕЛЕНЫ ПО ПЕРЕХОДНОЙ Ф_ЦИИ (хар-ке) и по ипульсной переходной хар-ке (ф-ци веса)

1.Переходная хар-ка h(t). Представляет собой перех процесс на выходе звена, возникающий при подаче на его вход сигнала в виде единичной ступенчатой функции

Переходная хар-ка м.б. определена экспериментально или аналитически. При аналитич определении перех хар-ки нужно найти решение диф-го ур-ия САУ или звена при вх сигнале в виде единичн ступенчатой функции и при нулевых начальных условиях. Перех хар-ка обыно представляется в виде графика. Конкретный вид переходной характеристики зависит от динамич свойств САУ или эл-та и м.б. весьма разнообразна

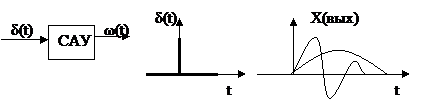2. Ф-ция веса или импульсная перех-ая хар-ка на импульсную фун-цию, которая подана на вход САУ или ее элемента

Импульсная перех-ая хар-ка м.б. получена диф-нием по времени переходной хар-ки 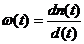как видно из этого выражения логарифм частотн передат функции равен комплексному выражению. Вещественной частью которого являетсаяс логарифм модуля, а мнимой – фаза. Для практических целей удобнее пользоваться десятичными логариф-ми и строить отдельно логариф-ую АЧХ или ЛФЧХ. Для построения ЛАЧХ определяется величина 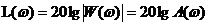- эта величина выражается в децибелах. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. 1 бел – увеличение мощности в 10 раз. Деци – десятая часть. Если бы А(ω) было отношением мощности, то перед lg в правой части должен был бы стоять множитель 10, но т.е. А(ω) представл собой отнош не мощности, а вых и вх величин (переем скор напр токов), то увеличение этого отнош в 10 раз будет соотв-ать увелич отнош мощности в 100 раз, что соотв-ет двум белам или 20 дБ. Для построения ЛАЧХ исп-ся стандартная сетка, по оси абсцисс откладывается частота в логар-ом масштабе, по оси ординат откладывается модуль в дБ.По оси ординат наносится равномерный масштаб ось абсцисс должна проходить через точку 0 дБ, что соотв-ет знач модуля а А(ω)=1, т.к. lg1=0

\\\график

Ось ординат модет пересекать ось абсцисс в произвольном месте, поэтому ось ординат проводят так, чтобы справа от нее м.б. показать весь ход ЛАЧХ. Ось абсцисс делится на декады и октавы. Декада-отрезок ось абсцисс, соответствующий десятикратному изменению частоты. Октава – отрезок ось абсцисс, соответс-ий двукратному изменению частоты.

13 Частотные характеристики.

Как и временнфые хар-ки, они широко используются при исследовании динамич cв-в САУ и их элементов. Частотн харки САУ определяют зависимость м/у вх и вых величинами в установившемся режиме при гармонич воздействии. В установившемся режиме исследовать свойства системы и судить об устойчивости системы и оценивать качество процесса управления. Важнейшей хар-кой димамич звена явл-ся его частотно-перидаточная ф-ция. Для ее построения рассмотрим динамич звено в случае, когда возмущающее воздействие на входе равно 0 f(t)=0 и на сис-му подается гармонич воздействие X Хвх(t)=Авхsin(ωt+φ), где φ – фазовый сдвиг м/у вх и вых колеб

φ(ω)

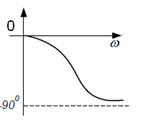
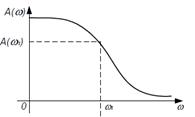
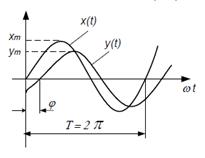При фиксированной амплитуде входных колебаний амплитуда и фаза установившихся колебаний на выходе зависят от частоты колебаний зависят от частоты колебаний вели постоянно увеличивать частоту колебаний и определ установившиеся значения амплитуды и фазы выходных колебаний, то можно получ зависимость отношения амплитуд от чсастоты, а также зависимость сдвигов фаз вых и вх установив колеб от частоты

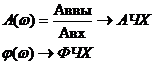
Рассмотренные частотные характеристики м.б. получены экспериментально или аналитически. Аналитич выраж для частотн хар-к получают из передаточной ф-ции. Если выраж. Передаточн ф-ции W(P) подставить P=lω, то получится комплексная передаточная ф-ция 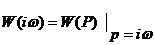Комплексная передаточн ф-ция явл-ся АФЧХ и представл собой комплексное число, модуль которого равен отношению амплитуды вых величины к амплитуде вх величины или АЧХ, а аргумент равен сдвигу фаз вых величины по отнош к входной, т.е. ФЧХ.. М.б. представл как в показательной так и в алгебраической форме.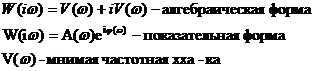

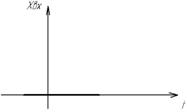
АФЧХ строится на компдексной плоскости, она представляет собой геом-ое место концов векторов (годограф), соотв-их частотно-передаточной ф-ции в алгебраич форме при изменении частоты от 0 до ∞

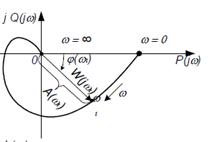По оси абсцисс откладыв-ся веществ часть V(ω), по оси ординат откладывается мнимая часть V(iω), для каждой частоты на комплексной плоскости наносится точка. Полученные точки соедин затем плавной кривой – годографом. Комплексная передаточной ф-ции при фиксированном значении частоты на компл-ой плоскости изобр вектором, а аргумент – значение фазы. При изменении частоты от 0 до ∞ конец вектора опишет кривую, которая представл собой график АФЧХ. Для оценки динаич свойств САУ и их Эл-тов АЧХ и ФЧХ обычно строятся в логарифмических координатах. Прологарифируем выраж частот перед ф-ции в показательном виде