Начальные и краевые условия.

Начальное условие – задание температуры во всех точках стержня в начальный момент: u(x,0)=f(x) Краевые условия – условия в тех точках стержня, где возможен теплообмен с окружающей средой – на торцевых сечениях стержня. Простейшие краевые условия – концы стержня поддерживаются при постоянной температуре:

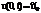
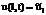
С учетом закона сохранения энергии получаем для правого торцевого сечения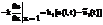

для левого торцевого сечения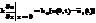

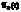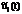Где и – заданные температуры внешней среды.

Таким образом, задача теплопроводности для однородного стержня с теплоизолированной боковой поверхностью без тепловых источников сводится к отысканию температуры u=u(x,t), удовлетворяющей уравнению

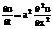начальному условию

u(x,0) = f(x)

краевым условиям

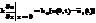
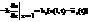
Уравнения параболического типа.

Пространственная задача теплопроводности.

Будем рассматривать неравномерно нагретое тело, температура которого в каждой точке (x,y,z) в момент времени t определяется функцией u(x,y,z,t). В фиксированный момент времени t совокупность точек, в которых 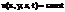Образует изотермическую поверхность. Направление наибольшей скорости изменения температуры u совпадает с направлением градиента функции u(x,y,z,t) при фиксированном значении t:

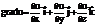
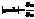
Величина теплового потока через малый участок 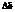изотермической поверхности за время 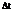равна

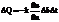
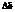- нормаль, единичный вектор

Здесь k – коэффициент теплопроводности.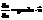

Тогда поток тепла через участок 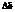любой поверхности за время 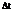будет равен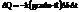

Если ввести вектор теплового потока

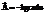то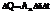

Если рассмотреть поток через замкнутую поверхность, то

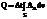
Применяя теорему Остроградского-Гаусса, получаем

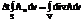де V – часть тела, ограниченная поверхностью S.

В результате 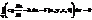Следовательно

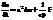Где 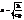основное уравнение теплопроводности.

Уравнения параболического типа.

Начальные и краевые условия.

Начальное условие – задание распределения температур во всех точках тела в начальный момент времени

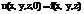
Краевое условие задается на поверхности G, ограничивающей тело. Поток тепла изнутри тела через любую часть поверхности тела G пропорционален перепаду температур на этой части границы: 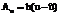где 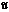– температура окружающей среды в граничащих с телом точках (G), h – коэффициент теплообмена. С учетом выражения

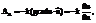получаем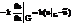

В частных случаях краевое условие упрощается. Например, h = 0, что соответствует теплоизолированной границе

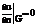Другой частный случай 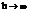, т.е. коэффициент внешней теплопроводности очень большой. Получаем

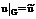что означает, что на границе тело имеет температуру внешней среды.

Задачи диффузии.

Концентрация – число атомов и молекул этого вещества в единице объема.

В задачах диффузии находится неизвестная функция – концентрация диффундирующего вещества, обозначаемая

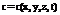
Процесс диффузии аналогичен теплопроводности, поэтому уравнение диффузии будет иметь вид

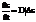Здесь D – коэффициент диффузии.

Начальные условия –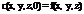

мы задаем начальную концентрацию. Краевые условия

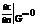соответствует тому, что граница G непроницаема для диффундирующего вещества, - концентрация на границе