Частные производные. Их геометрический и физический смысл.

Частной производной ф-ции ƶ=f(x;y) по аргументу х наз 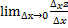предел отношения частного приращения ф-цииz по х к приращ аргумента х, т.е. к ∆х, если ∆х→0 и этот предел сущ.

Геометрич смысл: tg угла наклона касательной к линии пересечения пов-ти и пл-ти

α₁: 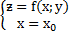к оси ОХ.

Физич. смысл: ƶ_х^’, ƶ_у^’- ск-ти изм-ся ф-ции ƶ в направлении оси ОХ и оси ОУ.

Полный дифференциал.

Дифференциалом 1-го порядка ф-ции ƶ=f(x;y) наз главная линейная часть полного приращения ф-цииdz.

Dz складывается из двух частных дифференциалов.

Частный диф-л по х: z_x^’dx=d_xz

Производная в данном направлении и градиент. Связь между ними.

Производной ф-цииz по напр 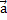наз:

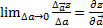
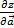=z_z^’cos£+z_y^’cosβ → произв. по напр. а

Градиентом ф-цииz в т.М₀наз вектор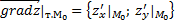

С учетом опр-я градиента произ-ая от z по напрa равна скалярному произв 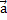на :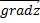

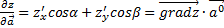
Экстремум функции двух переменных. Необходимые условия экстремума.

Говорят, что функция 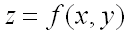имеет максимум в точке 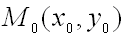, т.е. при 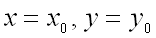, если 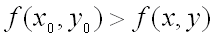для всех точек 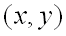, достаточно близких к точке 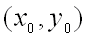и отличных от неё.
Говорят, что функция 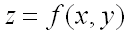имеет минимум в точке 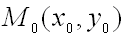, т.е. при 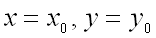, если 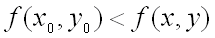для всех точек 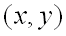, достаточно близких к точке 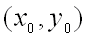и отличных от неё.
Максимум и минимум функции называются экстремумами функции.
Теорема (необходимое условие экстремума функции двух переменных). Если функция 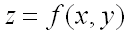достигает экстремума при 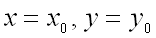, то каждая частная производная первого порядка от 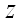или обращается в нуль при этих значениях аргументов, или не существует.
Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку 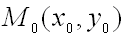функция 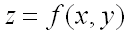имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка 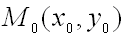является критической точкой функции 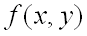, т.е.
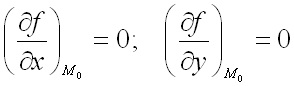, тогда при :
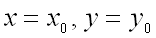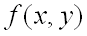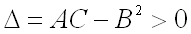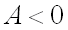1) имеет максимум, если дискриминант и , где ;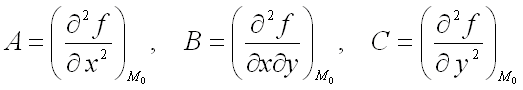
2) 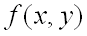имеет минимум, если дискриминант 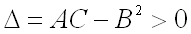и ;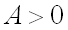
3) 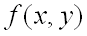не имеет ни минимума, ни максимума, если дискриминант ;
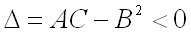4) если 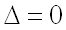, то экстремум может быть, а может и не быть (требуется дополнительное исследование)

Метод наименьших квадратов.

Этот метод является одним из наиболее распространенных приемов статистической обработки экспериментальных данных, относящихся к различным функциональным зависимостям физических величин друг от друга. В том числе, он применим к линейной зависимости и позволяет получить достоверные оценки ее параметров a и b, а также оценить их погрешности.

31.Задача об объёме цилиндрического тела. Задача о массе плоской пластинки. Понятие двойного интеграла. Теорема существования.

Двойным инт-лом от ф-цииf(x,y)по обл Д из пл-ти ХОУ наз предел последовательности инт-х сумм, если он сущ и не зависит от способа разбиения олб Д на ∆S_i и от выбора т.М(х_i, y_i) в них.

Теорема сущ: Если обл Д с кусочно-гладкой границей Г ограничена и замкнута, ф-цияz=f(x,y) непрерывна в Д, то она инт-ма в обл Д, т.е. сущ число I=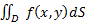

32. Свойства двойного интеграла. Вычисление двойного интеграла в прямоугольных координатах.

Св-ва: 1)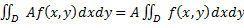

1) →