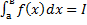Линейные дифференциальные уравнения 1-го порядка. Уравнения Бернулли.

ДУ1 наз линейным, если неизвестная ф-ция у(х) и ее производная у^’(х) входят в ДУ только в 1-ой степени.

Общий вид: a(x)y^’+b(x)y+c(x)=0 |:а(х)

Метод решения: метод Бернулли (у=uv).

Уравнение Бернулли. Общий вид: у^’+P(x)y=Q(x)y^£

Результат: 2 ур-ия с разд перемен.

11. Дифференциальные уравнения высших порядков. Общее и частное решения. Формулировка теоремы о разрешимости задачи Коши.

ДУ высшего порядка-это ДУ порядка выше певого. Общий вид:

F(x, y, y^’, y^’’… yⁿ)=0 →неявное задание

у⁽ⁿ⁾=f(x, y, y^’, y^’’… y^n-1)→ явное задание

Если f(x,y) и f^’_y(x,y) непрерывны в некобл-ти Dпл-ти f(x,y), то для любой т.М₀(х₀,у₀) сущ единое решение у(х) определенное в нек окрестности данной точки и удовлетворяющее условию у(х₀)=у₀

Простейшие дифференциальные уравнения, допускающие понижение порядка.

ДУ имеет вид: у⁽ⁿ⁾=f(x)

Метод инт-ия: n-кратное посл-оеинт-ие, при этом исп-ие у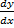^’= ; y^’’= ……

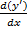13. Линейные дифференциальные уравнения. Линейные однородные уравнения. Фундаментальная система решений.

ДУ1 наз линейным, если неизвестная ф-ция у(х) и ее производная входят в ДУ только в 1-ой степени. Общий вид: а(х)у^’+в(х)у+с(х)=0 метод Бернулли.

ДУ любого порядка n наз. линейным, если неизвестная ф-цияу(х) и ее производные до n-го порядка входят в ур-ие в 1-ой степени.

Теорема о структуре общего решения линейного однородного дифференциального уравнения 2-го порядка.

Если ф-ция у₁, у₂ образуют фундаментальную систему решений ЛОДУII, то общее решение этого ур-ния будет линейная комбинация у=С₁у₁+С₂у₂, с₁, с₂- const

Теорема о структуре общего решения линейного неоднородного дифференциального уравнения 2-го порядка.

Общее решение ЛНДУIIсост из 2-х ф-ций: 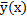- общее решение соот-го ЛОДУ2,

У_*(х)- к-либо частное решение исходного ЛНДУ2

Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.

Общий вид: y^’’+Py^’+Qy=0 → k²+Pk+Q=0:

a) D>0 → y(x)=C₁e^k1x+C₂e^k2x

b) D=0 → y(x)= C₁e^kx+C₂ xe^kx

c) D<0 → y(x)=e^£x(C₁cosβx+C₂sinβx)

17. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и с правой частью специального вида.Понятие о системах ЛДУ 1 порядка. Метод исключения.

f(x) наз ф-цией специального вида, если f(x)=e^£x (P_n(x)cosβx+Q_m(x)sinβx). £,β- действит числа; P_n(x), Q_m(x)- многочлены m,n степени.

ДУ любого порядка nназ линейным, если неизвестная ф-ция у(х) и ее производные до n-го порядка входят в ур-ие только в 1-ой степени.

18. Задача о площади криволинейной трапеции. Задача о работе переменной силы.Понятие определенного интеграла. Теорема существования.

Криволен. трапецией наз. плоская фигура, ограниченная отрезками прямых х=а, х=в, у=0 и кривой у=f(x)≥0 на [a,b].

ОИ наз. предел последовательности инт-х сумм вида 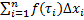при max 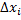→ (или n→ 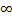), если этот предел сущ. и не зависит от способа разбиения [a;b] на части 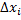и от выбора т. 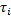в них.

Теорема сущ: Если ф-ция у=f(x) ограничена на [a;b], то она инт-ма в этом интервале, т.е. для нее сущинт-л: