Упражнение № 5. Расчет средней арифметической

Упражнение № 6. Расчет средней гармонической

Средняя гармоническая (простая) определяется формулой: 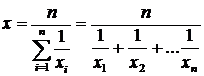. Для сгруппированных величин используется средняя гармоническая взвешенная: .

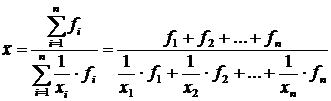Дано: автомобиль с грузом от предприятия до склада ехал со скоростью 40 км/час, а обратно порожняком - со скоростью 60 км/час.

Найти:среднюю скорость автомобиля за обе поездки.

Решение: пусть общее расстояние перевозки составляло s км, при замене индивидуальных значений скорости ( 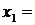40 км/час и 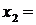60 км/час) на среднюю величину необходимо, чтобы неизменной величиной оставалось время, затраченное на обе поездки:

Общее время поездок равно: 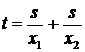или через среднюю скорость: 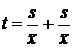, откуда: 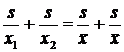или ,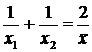

в результате получается: 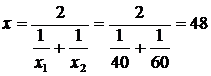км/час [4].

1. Перейти на чистый лист.

2.Для автоматизированного расчета результатов решения задачи в ячейки А7:D7соответственно ввести: Скорость, Туда, Обратно, Средняя. В ячейки В8:C8соответственно ввести:40, 60. Выделить их цветом и границами обрамления.

3.В ячейку D8(используя мастер функций) ввести формулу для расчета средней гармонической скорости =СРГАРМ(B8:C8).

Упражнение № 7. Расчет средней геометрической

Средняя геометрическая (простая) определяется формулой: 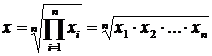. Для сгруппированных величин используется средняя геометрическая взвешенная: .

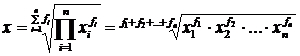Дано: выпуск продукции промышленного предприятия представлен по годам в таблице:

Таблица 8

Год	1995 г.	1996 г.	1997 г.
Объем продукции, тыс. руб

Найти:во сколько раз в среднем ежегодно увеличивался выпуск продукции.

Решение:

q для 1996 года увеличение объема выпуска по сравнению с предыдущим (1995 г) составило: 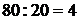(раза),

q для 1997 года увеличение объема выпуска по сравнению с предыдущим (1996 г) составило: 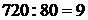(раз).

Ø Итого за 2 года (т.е. в 1997 г. по сравнению с 1995 г.) увеличение объема выпуска продукции составило: 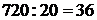(раз).

В среднем ежегодно объем выпуска возрастал в 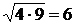(раз) ( 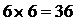) [4].

1.Перейти на чистый лист.

2.Для автоматизированного расчета результатов решения задачи в ячейки А10:А13соответственно ввести: Год, Объем, Рост. В ячейки В10:D10соответственно ввести годы:1995, 1996, 1997; в ячейки В11:D11числа, соответствующие объему производства: 20, 80, 720и выделить их цветом и границами обрамления.

3.В ячейку В12 ввести раз, в ячейку С12 ввести формулу, рассчитывающую во сколько раз возрос объем производства в 1996 г. по сравнению с 1997 г.: =C11/B11. Установить курсор в правый нижний угол ячейки С12, когда он примет крестообразный вид нажать и, удерживая нажатой левую кнопку мыши, протянуть его в ячейку D12 (тем самым копируя формулу для подсчета отношения для 1996 и 1997 годов). Выделить ячейки цветом и границами обрамления.

4.В ячейки F10 и F11соответственно ввести Среднийи рост. В ячейку F12 (используя мастер функций) ввести формулу, рассчитывающую среднее геометрическое ежегодное возрастание объема производства, =СРГЕОМ(C12:D12). Выделить ячейки цветом и границами обрамления.

Упражнение № 5. Расчет средней арифметической

Средней величиной называется обобщенный показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных условиях места и времени. Средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц совокупности.

Замена множества различных индивидуальных значений признака средним показателем позволяет выявить закономерности, присущие массовым явлениям, которые незаметны в единичных. Объективность и типичность статистической средней обеспечивается соблюдением условий:

ü средняя должна вычисляться для качественно однородной совокупности, для чего необходима группировка данных;

ü для исчисления средних должны быть использованы массовые данные.

Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности. В экономических исследованиях и плановых расчетах применяются 2 категории средних:

Ø степенные средние: средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадратическая;

Ø структурные средние: мода, медиана.

Степенные средние связаны неравенством: .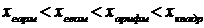

Средняя арифметическая (простая) определяется формулой: .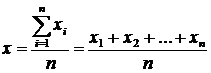

Для сгруппированных величин используется средняя арифметическая взвешенная:

.

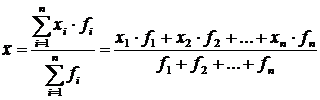Дано: имеется распределение рабочих участка по стажу работы:

Таблица 7

Стаж работы, лет	до 5 лет	5 - 10	10 - 15	15 - 20
Количество рабочих

Найти:средний стаж рабочих участка.

Решение:

Ø Для каждого интервала рассчитывается среднее значение признака как полусумма нижнего и верхнего значений интервала:

q для 1 интервала: ,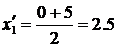

q для 2 интервала: ,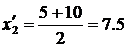

q для 3 интервала: ,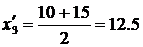

q для 4 интервала: .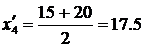

Ø По формуле средней взвешенной рассчитывается средний стаж работы:

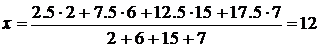(лет) [4].

1.Перейти на чистый лист.

2. Для автоматизированного расчета результатов решения задачи в ячейки А1:А3соответственно ввести: Стаж, работы, Количество. В ячейки В1:В2соответственно ввести:0, 5; в ячейки С1:С2числа: 5, 10; в ячейки D1:D2 ввести: 10, 15 и в ячейки E1:E2 ввести: 15, 20. В ячейки B3:E3ввести числа, соответствующие количеству рабочих в интервалах по стажу: 2, 6, 15, 7и выделить их цветом и границами обрамления.

3.В ячейку А5 ввести Полусумма, в ячейку В5 (используя мастер функций) ввести формулу, подсчитывающую полусумму значений интервала по стажу =СРЗНАЧ(B1:B2).

4.Установить курсор в правый нижний угол ячейки В5,когда он примет крестообразный вид, нажать и, удерживая нажатой левую кнопку мыши, протянуть его в ячейку Е5 (тем самым копируя формулу для подсчета среднего значения для других интервалов). Выделить ячейки цветом и границами обрамления.

5.В ячейки G1 и G2соответственно ввести Среднийи Стаж. В ячейку G3 (используя мастер функций) ввести формулу, рассчитывающую средний стаж работы в целом по участку, =СУММПРОИЗВ(B3:E3;B5:E5)/СУММ(B3:E3). Выделить ячейки цветом и границами обрамления.