Абсолютная и условная сходимость.

Перейдём теперь к рядам с членами, имеющими любой знак. С каждым таким рядом

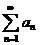(1)

связан ряд с неотрицательными членами, составленный из модулей членов данного ряда, т.е. ряд

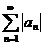(2)

Определение.Ряд (1) называется абсолютно сходящимся, если ряд (2) сходится. Если же ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся.

Теорема 1. Если ряд сходится абсолютно, то он сходится.

.

Функциональные ряды.

Будем рассматривать ряды, членами которых являются не числа, а функции:

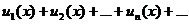(1)

Такие ряды называются функциональными.

Например, ряд

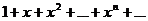
является функциональным.

Если в ряде (1) положим 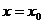, где 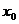- значение из области определения функций 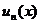, , 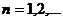то получим числовой ряд

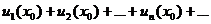(2)

Если ряд (2) сходится, то 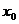называется точкой сходимостиряда (1). Если же ряд (2) расходится, то точка 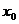называется точкой расходимости ряда (1).

Определение.Совокупность всех точек сходимости функционального ряда называется областью его сходимости.

Степенные ряды.

Определение. Степенным рядомназывается функциональный ряд вида

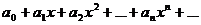, (1)

где 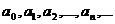- действительные числа, называемые коэффициентами степенного ряда.

А) Если степенной ряд сходится лишь в точке 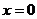, то он относится к рядам первого класса.

Например, ряд

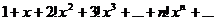(2)

относится к рядам первого класса. Зафиксируем 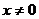и рассмотрим числовой ряд

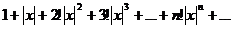
По признаку Даламбера

= =

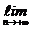
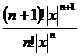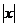
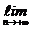
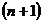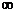
и ряд расходится при всех 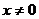. Следовательно, ряд (2) сходится только при .

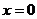Б)Если ряд (1) сходится на всей числовой прямой, то он относится к рядам второго класса.

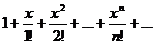Например, применив признак Даламбера при фиксированном 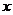нетрудно убедится, что к рядам второго класса относится ряд

В)Ряд (1), не принадлежит первому и второму классам, относят к рядам третьего класса.

Теорема Абеля. Если степенной ряд (1) сходится при 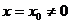, то он абсолютно сходится для любого 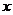, удовлетворяющего условию

;

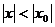если же степенной ряд (1) расходится при 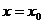, то он расходится и при любом 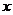, удовлетворяющем условию .

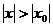Следствие.Для каждого степенного ряда (1) третьего класса существует число 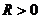, называемое радиусом сходимостиэтого ряда, для которого выполняется условия: при 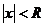ряд (1) сходится абсолютно, при 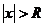ряд (1) расходится.

Промежуток 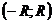называется интервалом сходимостистепенного ряда. Для степенного ряда (1) второго класса интервал сходимости .

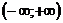Областью сходимостистепенного ряда (1) является интервал 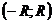, к которому в отдельных случаях добавляется один или оба конца этого интервала (это исследуется для конкретных рядом пр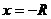и и ).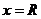

Для степенного ряда (1) первого класса полагают 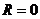; для степенного ряда (1) второго класса .

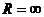Теорема 2. Пусть для степенного ряда (1) существует и отличен от нуля предел

.

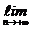
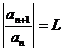б) 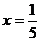. Имеем ряд = .

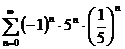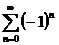Тогда

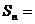
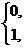
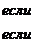
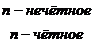
Поэтому 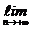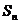не существует и ряд 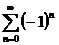расходится.

Итак, область сходимости ряда .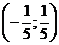

Основные понятия.

Дифференциальным уравнениемназывается соотношение, связывающее независимую переменную 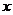, искомую функцию 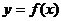и её производные. Если искомая функция есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным.Порядок старшей производной, входящей в дифференциальное уравнение, называется порядкомданного уравнения. Следовательно, общий вид ДУ n-го порядка следующий.

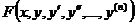=0. (1)

Например, уравнения

а) 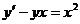б)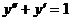

соответственно ДУ 1-го и 2-го порядков.

Функция 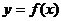, которая при подстановке её в уравнение (1) обращает это уравнение в тождество, называется решениемэтого уравнения.