Экстремум функции двух переменных.

Пусть функция z = 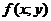определена в некоторой области D, точка .

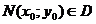Точка 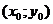называется точкой максимумафункции z = 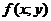, если существует такая 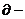окрестность точки 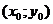, что для каждой точки 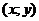, отличной от 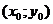, из этой окрестности выполняется неравенство: .

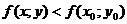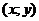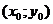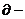Аналогично определяется точка минимумафункции: для всех точек , отличных от из окрестности точки 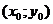выполняется неравенство: .

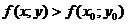Значение функции в точке в точке максимума (минимума) называется максимумом (минимумом)функции. Максимум и минимум называют её экстремумами.

Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный(местный) характер; значение функции в точке 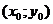сравнивается с её значениями в точках, достаточно близких к 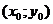. В области определения функция может иметь несколько экстремумов или не иметь ни одного.

Теорема(необходимые условия экстремума).

Если в точке 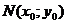дифференцируемая функция z = 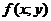имеет экстремум, то её частные производные в этой точке равны нулю: , .

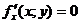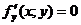Определение. Точка, в которой частные производные первого порядка функции

z = 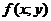равны нулю, т.е. 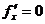, , 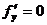называется стационарнойточкой функции z. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.

Для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию.

Теорема(достаточное условие экстремума).

Пусть в стационарной точке 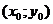и некоторой её окрестности функции 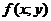имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке 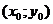значения 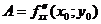, , 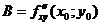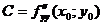. Обозначим

= .

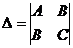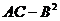Тогда:

1) если 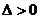, то функция 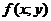в точке 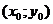имеет экстремум: максимум, если А<0: минимум, если А>0;

2) если 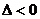, то функция 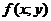в точке 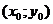экстремумов не имеет.

В случае, когда экстремум в точке 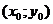может быть, а может и не быть.

Необходимы дополнительные исследования.

Метод наименьших квадратов.

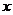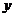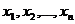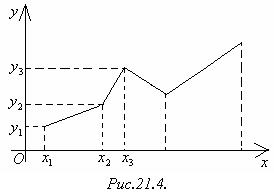
На практике при решении экономических задач зависимость между переменными и представляется в виде набора значений и соответствующих значений 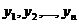. Эти значения изображаются точками плоскости с координатами 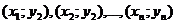. Ломаная линия, соединяющая эти точки, называются экспериментальной кривой(Рис.21.4).

Однако исследование характера и свойств зависимости между 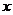и 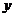лучше производить имея аналитическое задание этой зависимости 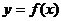, наиболее точно описывающей экспериментальные данные, определяется экономическими или иными соображениями. В качестве таких функций используются следующие:

1) 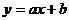─ линейная функция;

2) 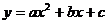─ параболическая функция;

3) 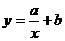─ гиперболическая функция;

4) 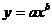─ показательная функция;

5) 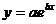─ экспоненциальная функция.

Выбранная для приближения функция называется теоретической. После выбора вида функции надо найти значения определяющих её параметров 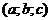таким образом, чтобы отклонения значений функции от экспериментальных значений были минимальными. Минимизацию отклонений обычно проводят, находя минимум суммы квадратов отклонений S = 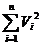, где 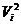= 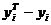─ отклонения теоретических значений функции от экспериментальных.

Общий метод наименьших квадратов для нахождения параметров на примере линейной функции: 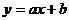. Для этой функции коэффициенты 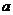и 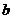находят из системы уравнений:

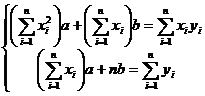
Решения этой системы дают минимум функции S = S 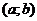, а сама система называется системой нормальных уравнений.Эта система линейная относительно неизвестных 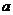, 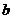и её определитель

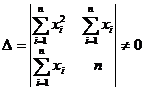
Следовательно, система имеет единственное решение, которое можно найти по правилу Крамера:

; .

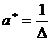
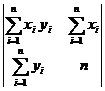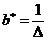
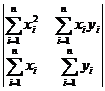Таким образом, наилучшим линейным приближением экспериментальной кривой по методу наименьших квадратов является прямая 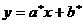, где 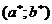─ решение системы нормальных уравнений.

Замечание.Если в качестве теоретической зависимости выбрана зависимость, отличная от линейной, то из условия 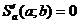, 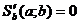находят соответствующую систему нормальных уравнений и решают её.