Взаимное расположение прямых в пространстве.

Пусть даны две прямые и .

Очевидно, что прямые лежат в одной плоскости тогда и только тогда, когда векторы 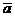, и компланарны, т.е.

= 0 (9)

Если в (9) первые две строки пропорциональны, то прямые параллельны. Если все три строки пропорциональны, то прямые совпадают. Если условие (9) выполнено и первые две строки не пропорциональны, то прямые пересекаются.

Если же ¹ 0, то прямые являются скрещивающимися.

Задачи на прямую и плоскость в пространстве.

Прямая как пересечение двух плоскостей.

Пусть заданы две плоскости

А₁х + В₁у +С₁z + D₁ = 0,

А₂х + В₂у +С₂z + D₂ = 0

Если плоскости не являются параллельными, то нарушается условие

.

Пусть, например ¹ .

Найдём уравнение прямой, по которой пересекаются плоскости.

В качестве направляющего вектора искомой прямой можно взять вектор

= × = = .

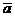Чтобы найти точку, принадлежащую искомой прямой, фиксируем некоторое значение

z = z₀ и решая систему

,

получаем значения х = х₀, у = у₀. Итак, искомая точка М(х₀;у₀;z₀).

Искомое уравнение

.

Взаимное расположение прямой и плоскости.

Пусть задана прямая х = х₀ + а₁t, y = y₀ + a₂t, z = z₀ + a₃t

и плоскость

А₁х + В₁у +С₁z + D₁ = 0.

Чтобы найти общие точки прямой и плоскости, необходимо решить систему их уравнений

откуда

А₁(х₀ + а₁t) + B₁(y₀ + a₂t) + C₁(z₀ + a₃t) + D₁ = 0,

(A₁a₁ + B₁a₂ + C₁a₃)t + (A₁x₀ + B₁y₀ + C₁z₀ + D₁) = 0.

Если А₁а₁ + В₁а₂ + С₁а₃ ¹ 0, то система имеет единственное решение

t = t₀ = - .

В этом случае прямая и плоскость пересекаются в единственной точке М₁(х₁;у₁;z₁), где

х₁ = х₀ + а₁t₀, y₁ = y₀ + a₂t₀, z₁ = z₀ + a₃t₀.

Если А₁а₁ + В₁а₂ + С₁а₃ = 0, А₁x₀ + В₁y₀ + С₁z₀ + D₁ ¹ 0, то прямая и плоскость не имеет общих точек, т.е. параллельны.

Если же А₁а₁ + В₁а₂ + С₁а₃ = 0, А₁x₀ + В₁y₀ + С₁z₀ + D₁ = 0, то прямая принадлежит плоскости.

Угол между прямой и плоскостью.

Найдём угол j между прямой

= =

и плоскостью А₁х + В₁у +С₁z + D₁ = 0.

Поскольку вектор 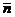= (А₁;В₁;С₁) образует с направляющим вектором 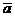= (а₁;а₂;а₃) угол y = 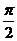- j или y = 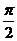+ j (Рис.10.3 и Рис.10.4), то cosy = cos( 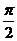- j) или cosy = cos( 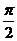+ j), откуда cosy = sinj или cosy = - sinj.

Значит, sinj = ôcosyô= .

Расстояние от точки до плоскости.

Пусть плоскость задана общим уравнением Ах +Ву + Сz +D = 0. Расстояние от точки М(х₀;у₀;z₀) до данной плоскости вычисляется по формуле

d = .

Цилиндры второго порядка.

Определение. Цилиндрической поверхностьюназывается поверхность, описываемая прямой (образующей),движущейся вдоль некоторой линии (направляющей) и остающейся параллельной исходному направлению.

Определение. Цилиндром второго порядканазывается цилиндрическая поверхность, направляющей которой является эллипс (окружность), гипербола или парабола.

Рассмотрим цилиндры второго порядка, у которых образующая параллельна оси Оz.

1). Эллиптический цилиндр (рис.10.5).

.

В частности эллиптический цилиндр имеет в качестве направляющей окружность. Его уравнение

или .

2). Гиперболический цилиндр(рис. 10.6)

-

.

3) Параболический цилиндр(рис. 10.7).

х² = 2ру.