Смешанное произведение векторов.

Определение. Пусть даны три вектора , и . Умножим вектор на векторно, а затем, векторное произведение × умножим скалярно на . В результате получим число ( × )× , которое называют смешанным произведениетрёх векторов , и .

Теорема 3.Смешанное произведение ( × )× трёх некомпланарных векторов равно объёму параллелепипеда, построенного на векторах , и , связанному со знаком «+», если тройка , , правая, и со знаком «−», если эта тройка ─ левая.

Доказательство. Рассмотрим параллелепипед, построенный на векторах , и (рис.9.5).

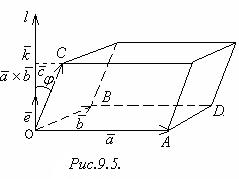
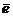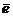Построим вектор × и пусть ─ единичный вектор, одинаково направленный с вектором × . Так как │ × │= S ─ площадь параллелограмма OBDA, построенного на векторах и , то × = ×S.

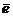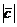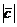Возьмём ось ℓ, одинаково направленную с вектором . Тогда по свойствам проекции векторов пр_е = соsφ, где φ ─ угол между и осью ℓ. Тогда │пр_е │= h, где h ─ высота параллелепипеда. Отметим, что если тройка , , правая (рис.9.5), то h = пр_е = = соsφ. Если же тройка , , левая, то h = − пр_е = − 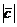соsφ.

Теперь,

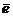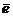( × )× = ( S)× = ( × )S = 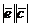cosφ × S = S × 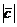соsφ = ± S × h = ± V_{параллелепипеда,}

причём знак «+» берётся, если , , ─ правая тройка, и знак «−», если она левая.

Следствие 3.1.Векторы , и компланарны тогда и только тогда, когда их смешанное произведение ( × )× = 0.

Доказательство.

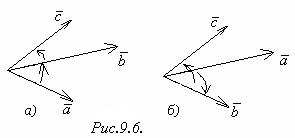
Отметим, что если тройка , , правая, то тройка , , также правая (рис.9.6(а)), а если тройка , , левая, то тройка , , также левая (рис.9.6(б)).

Очевидно, что параллелепипед, построенный на векторах , , и векторах , , ─ один и тот же. Поэтому

( × )× = ±V_парал., ( × )× = ± V_{паралл.}

Так как тройки , , и , , либо обе правые, либо обе левые, то знак перед V выбирается в обоих произведениях одинаково. Поэтому

( × )× = ( × )× = ×( × ).

Ввиду следствия 3.2 смешанное произведение векторов , , ещё обозначают .

Теорема 4.Если = (х₁;у₁;z₁), = (х₂;у₂;z₂), = (х₃;у₃;z₃), =

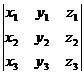
Доказательство.

= ( × )× = х₃ × 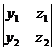− у₃ × 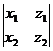+ z₃ × = .

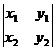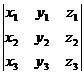Определение. Уравнением поверхностив заданной системе координат в пространстве называется такое уравнение с тремя переменными, которому удовлетворяют координаты любой точки данной поверхности и только они.

Поверхность, определяемая алгебраическим уравнением n-й степени относительно декартовых координат, называется поверхностью n-го порядка. Мы рассмотрим поверхности 1-го и 2-го порядков.

Плоскость в пространстве.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

Пусть дана точка М₀(х₀;у₀;z₀) и ненулевой вектор 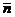= (А,В,С). Требуется составить

уравнение плоскости, проходящей через точку М₀ перпендикулярно указанному вектору 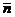(Рис.10.1). В таком случае вектор 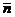называют нормальнымвектором плоскости.

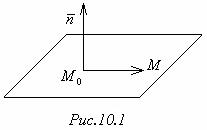Пусть М(х;у;z) ─ произвольная точка плоскости. Так как вектор 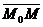= (х-х₀;у-у₀;z-z₀) лежит на плоскости, то он перпендикулярен вектору 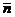. Следовательно, их скалярное произведение равно нулю, т.е.

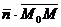= 0.

Тогда

А(х - х₀) + В(у - у₀) + С(z - z₀) = 0 (1)

Получили искомое уравнение.

Общее уравнение плоскости.

Раскроем скобки в уравнении (1):

А(х - х₀) + В(у - у₀) + С(z - z₀) = 0

Ах + Ву +Сz + (- Ах₀ – Ву₀ – Сz₀) = 0

Обозначим через D = - Ах₀ – Ву₀ – Сz₀ . Получаем уравнение

Ах + Ву +Сz + D = 0, (2)

которое называется общим уравнением плоскости.

Частные случаи:

1) D = 0. Уравнение Ах + Ву +Сz = 0 определяет плоскость, проходящую через начало координат.

2) С = 0. В этом случае нормальный вектор 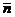(А;В;0) перпендикулярен оси Оz. Поэтому плоскость Ах + Ву + D = 0 параллельна оси Оz.

3) С = 0, D = 0. С учётом п.1) и п.2) плоскость Ах +Ву = 0 проходит через ось Oz.

4) В = 0, С = 0. В этом случае нормальный вектор 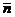(А;0;0) перпендикулярен плоскости Oyz. Поэтому плоскость Ах + D = 0 параллельно оси Oyz.

5) В = 0, С = 0, D = 0. Плоскость Ах = 0 или х = 0 определяет координатную плоскость Oyz.

Аналогично рассматриваются всевозможные другие случаи.