Связь между полярными и декартовыми координатами.

Чтобы установить связь между полярными координатами точки и её прямоугольными координатами, будем предполагать, что начало прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка М имеет прямоугольные координаты х₀ и у_о и полярные координаты r и j (рис.1.3).

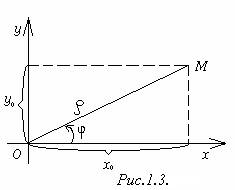
Нетрудно доказать, что при любом расположении точки М, верны равенства

х₀ = rcosj, у₀ = rsinj. (1)

Формулы (1) выражают прямоугольные координаты через полярные. Выражения полярных координат через прямоугольные следуют из формул (1):

r = 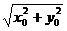, tgj = 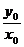. (2)

Заметим, что формула tgj = 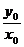определяет два значения полярного угла j, т.к. 0≤j<2p. Из этих двух значений угла j выбирают то, при котором удовлетворяются равенства (1).

Расстояние между двумя точками.

Пусть задана прямоугольная система координат.

Теорема 1.1.Для любых двух точек М₁(х₁;у₁) и М₂(х₂;у₂) плоскости расстояние d между ними выражается формулой

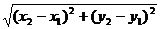d = . (3)

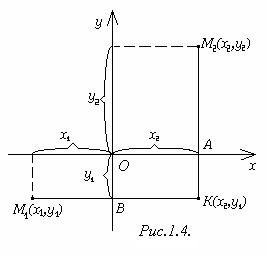
Доказательство.Опустим из точек М₁ и М₂ перпендикуляры М₁В и М₂А соответственно на оси Оу и Ох и обозначим через К точку пересечения прямых М₁В и М₂А (рис.1.4). Возможны следующие случаи:

1)Точки М₁, М₂ и К различны. Очевидно, что точка К имеет координаты (х₂;у₁). Нетрудно заметить что М₁К = ôх₂ – х₁ô, М₂К = ôу₂ – у₁ô. Т.к. ∆М₁КМ₂ прямоугольный, то по теореме Пифагора d = М₁М₂ = = = .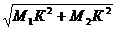

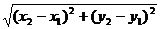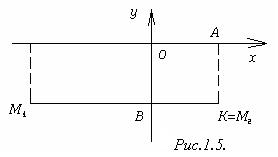2) Точка К совпадает с точкой М₂, но отлична от точки М₁ (рис.1.5). В этом случае у₂ = у₁ и

d = М₁М₂ = М₁К = ôх₂ – х₁ô= = = .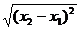

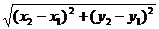3) Точка К совпадает с точкой М₁, но отлична от точки М_{2 .} В этом случае х₂ = х₁ и

d =М₁М₂ = КМ₂ = ôу₂- у₁ô= = .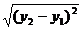

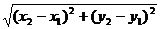4) Точка М₂ совпадает с точкой М₁. Тогда х₁ = х₂ , у₁ = у₂ и

d = М₁М₂ = О = .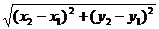

Деление отрезка в данном отношении.

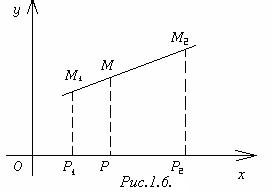Пусть на плоскости дан произвольный отрезок М₁М₂ и пусть М ─ любая точка этого отрезка, отличная от точки М₂ (рис.1.6). Число l, определяемое равенством l = = 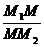, называется отношением, в котором точка М делит отрезок М₁М₂.

Теорема 1.2.Если точка М(х;у) делит отрезок М₁М₂ в отношении l, то координаты этой точки определяются формулами

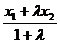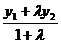х = , у = ,(4)

где (х₁;у₁) ─ координаты точки М₁, (х₂;у₂) ─ координаты точки М₂.

Доказательство.Докажем первую из формул (4). Вторая формула доказывается аналогично. Возможны два случая.

1) Прямая М₁М₂ перпендикулярна оси Ох. Тогда х₁ = х = х₂ и поэтому

х = х₁ = = = .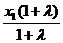

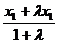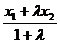2) Прямая М₁М₂ не перпендикулярна оси Ох (рис.1.6). Опустим перпендикуляры из точек М₁, М, М₂ на ось Ох и обозначим точки их пересечения с осью Ох соответственно Р₁, Р, Р₂. По теореме о пропорциональных отрезках 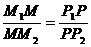= l.

Т.к. Р₁Р = ôх – х₁ô, РР₂ = ôх₂ – хô и числа (х – х₁) и (х₂ – х) имеют один и тот же знак (при х₁ < х₂ они положительны, а при х₁ > х₂ отрицательны), то

l = = ,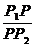

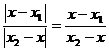х – х₁ = l(х₂ – х), х + lх = х₁ + lх₂,

х = .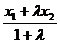

Следствие 1.2.1.Если М₁(х₁;у₁) и М₂(х₂;у₂) ─ две произвольные точки и точка М(х;у) ─ середина отрезка М₁М₂, то

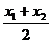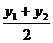х = , у = . (5)

Доказательство. Так как М₁М = М₂М, то l = 1 и по формулам (4) получаем формулы (5).

Площадь треугольника.

Теорема 1.3.Для любых точек А(х₁;у₁), В(х₂;у₂) и С(х₃;у₃), не лежащих на одной

прямой, площадь S треугольника АВС выражается формулой

S = 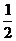ô(х₂ – х₁)(у₃ – у₁) – (х₃ – х₁)(у₂ – у₁)ô. (6)

Доказательство.Площадь ∆ АВС, изображённого на рис.1.7, вычисляем следующим образом:

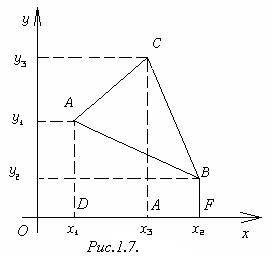S_ABC = S_ADEC + S_BCEF – S_ABFD.

Вычисляем площади трапеций:

S_ADEC = ,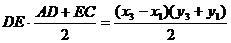

S_BCEF = ,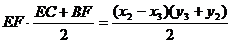

S_ABFD = .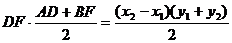

Теперь имеем

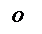S_ABC = 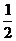((х₃ – х₁)(у₃ + у₁) + (х₂ – х₃)(у₃ + у₂) - (х₂ –

– х₁)(у₁ + у₂)) = 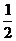(х₃у₃ – х₁у₃ + х₃у₁ – х₁у₁+ х₂у₃ –

– х₃у₃ + х₂у₂ – х₃у₂ – х₂у₁ + х₁у₁ – х₂у₂ + х₁у₂) =

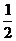= (х₃у₁ – х₃у₂ + х₁у₂ – х₂у₁ + х₂у₃ – х₁у₃) = 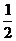(х₃(у₁ – у₂) + х₁у₂ – х₁у₁ + х₁у₁ – х₂у₁ + у₃(х₂ – – х₁)) = 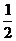(х₁(у₂ – у₁) – х₃(у₂ – у₁) + у₁(х₁ – х₂) – у₃(х₁ – х₂)) = 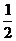((х₁ – х₃)(у₂ – у₁) + (х₁ –

– х₂)(у₁ – у₃)) = 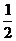((х₂ – х₁)(у₃ – у₁) – (х₃ – х₁)(у₂ – у₁)).

Для другого расположения ∆ АВС формула (6) доказывается аналогично, но может получиться со знаком «-». Поэтому в формуле (6) ставят знак модуля.