Решение краевой задачи методом пристрелки

В методе пристрелки рассматривается двухточечная краевая задача для системы дифференциальных уравнений

,

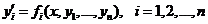или в векторной форме

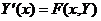. (24)

В качестве краевых условий заданы значения искомых функций 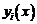на концах отрезка 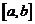, причем часть условий задана в точке a, а другая часть - в точке b:

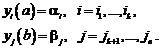
Числа i и j могут частично или даже полностью совпадать; однако между собой все числа i различны, также как и числа j.

Метод состоит в сведении краевой задачи к задаче (или задачам) Коши. Для того, чтобы можно было решать задачу Коши, исходя из точки a, нужно добавить недостающие (n–k) условий – значений неизвестных функций в точке a. При отсутствии каких-либо предположений относительно недостающих условий, эти условия выбираются произвольным образом. Аналогично добавляется k недостающих значений неизвестных функций в точке b. Тем самым формируется вектор недостающих или добавленных параметров P, часть координат которого относится к точке a, и часть к точке b. После добавления недостающих параметров – добавления недостающих условий – можно решать задачу Коши, как исходя из точки a, так и исходя из точки b, – навстречу друг другу.

Обозначим:

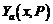– решение задачи Коши, исходящее из точки a при заданном значении вектора P,

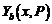– решение, исходящее из точки b.

Если добавленные условия (координаты вектора P) выбраны правильно, то 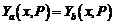во всех внутренних точках отрезка 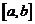. Если добавленные условия неверны, то существует расхождение: 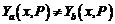. Поэтому задача состоит в поэтапном улучшении первоначально добавленных условий – корректировке координат вектора P – до тех пор, пока решения не совпадут. В этом и состоит суть метода пристрелки.

Для решения задачи выбираем точку сшивания 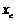. Если координаты вектора P выбраны правильно, то выполняется равенство:

.

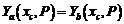В общем случае существует невязка:

.

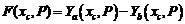Цель состоит в решении системы уравнений:

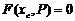, (25)

т.е. в нахождении такого значения вектора P, при котором невязка равна нулю. Если это решение найдено, то любая из функци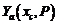й: или 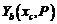– является решением исходной краевой задачи.

Решение системы (25) находят каким-либо итерационным методом, например, методом Ньютона. Обозначим:

P^s – значение вектора недостающих параметров на шаге итераций с номером s,

F^s = F(x_c,P^s) – соответствующее значение вектора невязки.

В соответствии с методом Ньютона приближение с номером s+1вычисляется по формуле:

P^s+1 = P^s – (J^s)^–1 * F^s, (26)

где 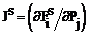- значение матрицы частных производных на шаге итераций с номером s.

Отметим, что вместо вычислений по формуле (26) предпочтительнее решать систему линейных алгебраических уравнений относительно вектора приращений DP^S = P^S+1 – P^S:

J^S *DP^S = -F^S, (27)

т.к. вычисление обратной матрицы (J^S)^–1 требует большего объема вычислений, чем решение системы (27).

Итак, начиная с выбранного нулевого приближения 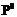, можно найти решение уравнения (25) с требуемой точностью. Однако трудность состоит в том, что неизвестно аналитическое выражение для невязки: на каждом шаге итераций – невязка представлена только набором из n чисел. Поэтому вместо точных значений частных производных приходится использовать их оценки. Для получения этих оценок координатам вектора недостающих параметров поочередно даются приращения, и для каждого приращения вновь решается задача Коши. Обозначим:

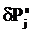– приращение j-ой координаты вектора недостающих параметров на s-ом шаге итераций,

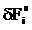– приращение i-ой координаты вектора невязки.

Тогда отношение 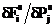дает оценку значения частной производной 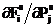. Таким образом, приращение одной из координат вектора P^S и повторное решение задачи Коши позволяет найти один из столбцов матрицы J^S. Для нахождения всех столбцов матрицы следует решить задачу Коши (n+1) раз на каждом шаге итераций.

В случае, когда решение задачи Коши устойчиво на отрезке [a,b], размерность задачи может быть уменьшена. Для этого в качестве точки сшивания выбирается одна из границ отрезка. При этом размерность вектора P может выть снижена до m = min(k, n-k). В частности, для дифференциального уравнения 2-го порядка (или для системы из двух уравнений 1-го порядка) вектор недостающих параметров сводится к скаляру.

Отметим, что при решении линейной краевой задачи достаточно выполнить один шаг итераций.

Вычисление интегралв