Тема: Численные методы решения нелинейных уравнений

Все численные методы являются методами уточнения корней, так что применению любого численного метода должно предшествовать определение интервала изоляции корня.

Отделение корней обычно выполняют графически: определяют точки пересечения графика функции с осью абсцисс. Можно это сделать и аналитически: определить корни первой производной функции, т. е. выделить точки смены знака производной, и составить таблицу знаков функции. Интервалы, на которых функция меняет знак, и определят исходные интервалы изоляции действительных корней уравнения.

Свойства функции на интервале изоляции, содержащем единственный корень уравнения:

- функция на концах интервала имеет разные знаки;

- первая и вторая производные функции не меняют знаки.

Метод хорд

Для реализации сходящегося процесса уточнения корня используют две расчётных формулы. Выбор формулы и нулевого приближения определяется знаком второй производной функции на интервале изоляции корня.

Пусть решается нелинейное уравнение 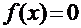и известен интервал изоляции одного из его корней - 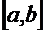. Для выбора расчётной формулы следует определить знаки функции на концах интервала, т. е. 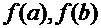, и знак второй производной на интервале - .

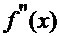Из графической интерпретации метода хорд следует, что при уточнении корня один конец интервала изоляции остаётся неподвижным, и это тот конец, на котором знак функции совпадает со знаком второй производной. Тогда противоположный конец интервала следует брать за нулевое приближение к корню.

Когда неподвижна точка 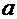, т. е. 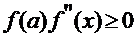, расчётная формула:

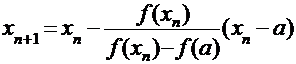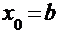; и . (1)

Когда неподвижна точка 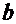, т. е. 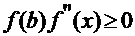, расчётная формула:

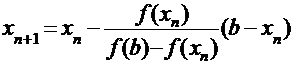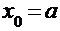; и . (2)

При ручных расчётах целесообразно вычисления вести в следующих таблицах.

По формуле (1): зафиксировать 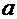; вычислить 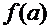; ввести обозначение 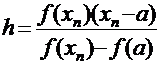; расчётная формула: .

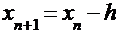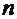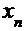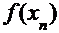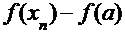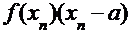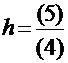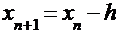По формуле (2): зафиксировать 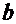; вычислить 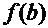; ввести обозначение 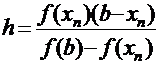; расчётная формула: .

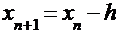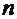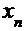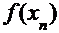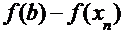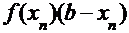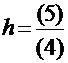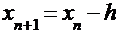Контроль за правильностью вычислений следует вести в таблице по следующим признакам:

- числовые значения в столбце 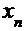не должны выходить за пределы интервала изоляции корня, т. е. при 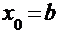значения 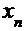должны приближаться к 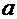,а при 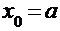значения 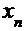должны приближаться к ;

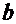- числовые значения в столбце 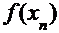должны приближаться к нулю с одной стороны;

- числовые значения в столбце 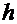должны уменьшаться по модулю на каждом шаге уточнения корня.

Расчёт следует закончить при достижении заданной точности, когда будет выполнено условие: .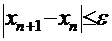

Следить за точностью приближения к корню по приведённой выше формуле можно лишь в случае, если на интервале изоляции соблюдается следующее неравенство: ,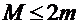

где ;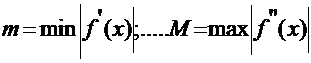

Если это неравенство не выполняется, интервал изоляции следует сузить. Если же не выполнять сужение интервала изоляции, то следить за точностью приближения к корню следует по общей более сложной формуле: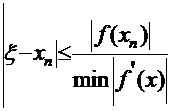

Пример 1. Найти корень нелинейного уравнения с точностью до 10^-4, применив метод хорд, на интервале изоляции [0,02;0,92]:

.

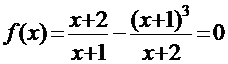Решение.

Знаки функции на концах интервала изоляции: 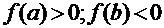. Знак второй производной 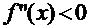, значит, правый конец интервала неподвижен, и за нулевое приближение в методе хорд следует взять противоположный конец - точку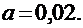

Проверим выполнение неравенства: 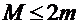, для чего вычислим минимум 1-ой производной - 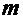=2,2449 и максимум 2-ой производной - 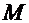=1,6371 на интервале изоляции корня. Неравенство выполняется, и за точностью приближения к корню можно следить по величине разности между двумя последовательными приближёнными значениями: .

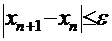Вычисления приведены в таблице, где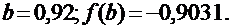

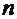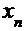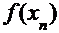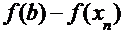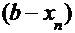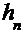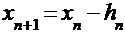	0,02 0,5753 0,6148 0,6178 0,6180	1,4550 0,1168 0,0090 0,0007 0,0001	-2,3581 -1,0199 -0,9121 -0,9038 -0,9032	0,0900 0,3447 0,3052 0,3022 0,3020	-0,5553 -0,0395 -0,0030 -0,0002	0,5753 0,6148 0,6178 0,6180 0,6180

Метод касательных Ньютона

Расчётная формула: .

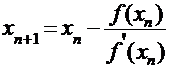Этот метод также требует сужения интервала изоляции до выполнения неравенства: 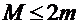. За нулевое приближение следует брать неподвижный конец интервала изоляции корня, иначе процесс приближения к корню будет расходящимся.

Расчётная таблица имеет следующий вид.

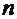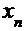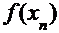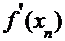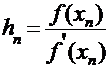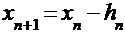Приме 2.. Найти корень нелинейного уравнения с точностью до 10^-5 методом касательных: 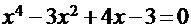на интервале [-3;-2].

Решение.

На концах интервала изоляции функция имеет разные знаки: 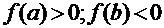; знак второй производной 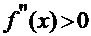. Значит, неподвижным является левый конец интервала – точка 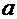, который в методе касательных и станет нулевым приближением к корню .

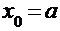Для выполнения неравенства 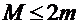необходимо сузить интервал изоляции до [-2,31;-2,29], тогда 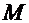=58,0332, 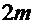=60,5919.

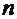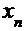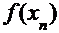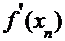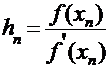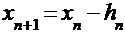	-2,310000 -2,302824 -2,302776	0,225663 0,001491 0,000000	-31,445564 -31,030526 -31,027757	-0,007176 -0,000048 -0,000000	-2,302824 -2,302776 -2,302776

Метод итераций

Этот метод требует приведения исходного уравнения к каноническому виду: 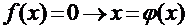. Тогда одношаговый итерационный процесс строится по формуле: 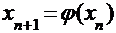при выборе любого нулевого приближения из интервала изоляции.

Главное - проверка соблюдения условий сходимости для канонического уравнения: 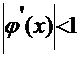- это обеспечит сходящийся итерационный процесс и получение значения корня уравнения с требуемой точностью за конечное число шагов.

Существует стандартный приём преобразования уравнения к каноническому виду, обеспечивающий сходимость итерационного процесса. 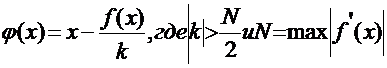. Знак 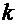совпадает со знаком первой производной исходной функции. Итерации продолжают до тех пор, пока не будет выполнено условие:

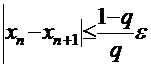, где 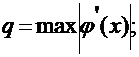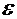- погрешность.

Если функция 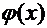возрастает, приближённые значения сходятся к точному значению корня монотонно, если же функция 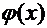убывает, то приближённые значения колеблются вокруг точного значения.

Пример 3.

Для функции 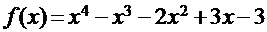найти интервалы изоляции действительных корней и на каждом интервале привести исходное уравнение к каноническому виду, используя стандартный приём, и проверить выполнение условий сходимости итерационного процесса.

Решение.

Построение графика функции выявило два действительных корня уравнения на интервалах [-2;-1] и [1;2].

Для применения стандартного приёма преобразования уравнения к каноническому виду необходимо найти максимум первой производной:

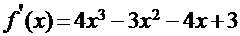
Интервал [-2;-1] : .

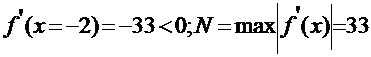Следовательно, положим 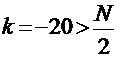и знак совпадает со знаком .

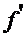Тогда правая часть канонического уравнения:

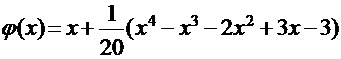
Проверим выполнение условия сходимости:

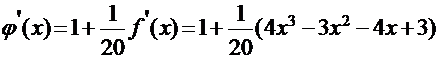
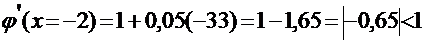
Интервал [1;2] : .

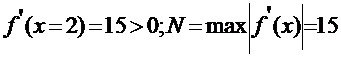Следовательно, положим 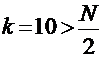и знак совпадает со знаком .

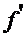Тогда правая часть канонического уравнения:

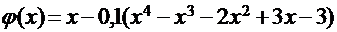
Проверим выполнение условия сходимости:

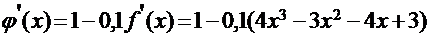
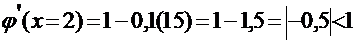
Таким образом, на каждом из интервалов условия сходимости выполняются для канонических уравнений, которые получены с помощью стандартной схемы преобразования исходного уравнения.

Пример 4. Найти корень нелинейного уравнения 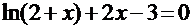на интервале [0,1;1] с точностью до 10^-5.

Решение. Для приведения исходного уравнения к каноническому виду можно использовать стандартный приём, а можно попробовать выразить 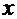из уравнения и проверить выполнение условия сходимости.

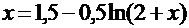
Сходимость итерационного процесса обеспечена, если 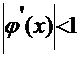. Найдём первую производную от правой части канонического уравнения.

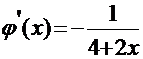
Вычислим значения производной на концах интервала 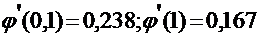- условия сходимости выполняются, следовательно, итерационный процесс будет сходящимся.

Выберем начальное приближение 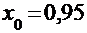и последующие вычисления представлены в таблице. Расчётная формула: .

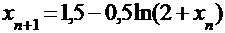n		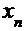	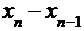комментарий
	0,95000000
	0,95909741	0,00909741	>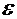
	0,95755785	0,00153956	>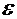
	0,95781806	0,00026021	>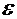
	0,95777407	0,00004399	>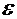
	0,95778151	0,00000744	<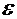

Значение корня с точностью 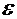=0,00001: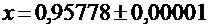

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1