Свойства пределов функции. Вычисление пределов.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

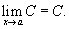
2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

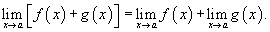
Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

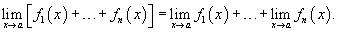
Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

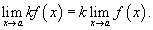
4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

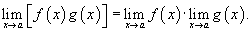
Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

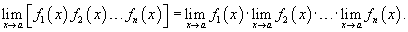
5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

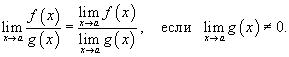
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ НА ОСНОВЕ ОПРЕДЕЛЕНИЯ ПРЕДЕЛА

Пример 1. Докажем, что

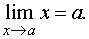
Пусть задано произвольное e>0. Тогда для того чтобы выполнялось неравенство

|f(x)-a|<e, необходимо выполнение неравенства |x-a|<e, которое, очевидно, выполняется, если |x-a|<d, где d=e. Таким образом, согласно определению предела функции, число a, действительно, является пределом функции x при x стремящемся к a.

Пример 2. Докажем, что

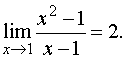
Нужно доказать, что при произвольном e>0 найдется такое положительное d, что неравенство

будет выполняться, если |x-1|<d. Но, если x не равно 1, то (1) эквивалентно неравенству

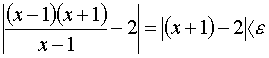
или

При произвольном e неравенство (1) будет выполняться, если будет справедливо (2), а последнее справедливо, если |x-1|<d, где d=e. Поэтому в соответствии с определением предела функции данная функция при x стремящемся к 1 имеет пределом число 2.

Определение числового ряда.

Сумма числового ряда 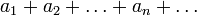определяется как предел, к которому стремятся суммы первых nслагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится. Элементы ряда представляют собой либо вещественные, либо комплексные числа.

Определение

Пусть 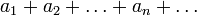— числовой ряд. Число 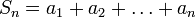называется 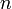-ой частичной суммойряда .

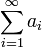Сумма (числового) ряда — это предел частичных сумм 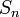, если он существует и конечен. Таким образом, если существует число 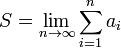, то в этом случае пишут 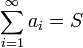. Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то говорят, что ряд расходится.

Сходимость числовых рядов

Свойство 1. Если ряд

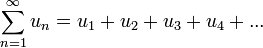(1.1)

сходится и его сумма равна S, то ряд

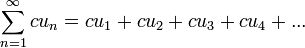(1.2)

где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится.

Свойство 2. Если сходится ряд (1.1) и сходится ряд

,

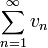а их суммы равны 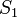и 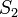соответственно, то сходятся и ряды

,

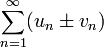причём сумма каждого равна соответственно .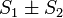

Необходимый признак сходимости ряда

Ряд 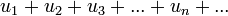может сходиться лишь в том случае, когда член 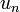(общий член ряда) стремится к нулю:

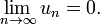
Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.