Определение матрицы, элементы матрицы.
Определение матрицы, элементы матрицы.
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Матрицы допускают следующие алгебраические операции:
сложение матриц, имеющих один и тот же размер;
умножение матриц подходящего размера (матрицу, имеющую столбцов, можно умножить справа на матрицу, имеющую строк);
умножение матрицы на элемент основного кольца или поля (т. е. скаляр).
Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом (векторное пространство над полем). Множество квадратных матриц замкнуто относительно матричного умножения, поэтому квадратные матрицы одного размера образуют ассоциативное кольцо с единицей относительно матричного сложения и матричного умножения.
Матрица представляет собой матрицу некоторого линейного оператора: свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.
В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.
Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.
Квадратная матрица.
КВАДРАТНАЯ МАТРИЦА [square matrix] — m × n матрица, у которой число строк и столбцов равно, т. е. m = n (индекс строки i = 1,2,..., m, а индекс столбца j = 1,2,..., n). Все элементы, для которых i=j, начиная со стоящего в левом верхнем углу элемента с индексами (1,1) и заканчивая стоящим в правом нижнем углу элементом с индексами (n,n), называются элементами главной диагонали. Для экономических приложений важно, что такая матрица имеет определитель (или детерминант) — число, получаемое из ее элементов по определенному правилу, и если определитель не равен нулю,
Определение суммы двух матриц, вычисление суммы.
Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

Умножение матрицы на число.

Произведение двух матриц.

Системы линейных уравнений.

Длина дуги плоской кривой
Дифференциал функции
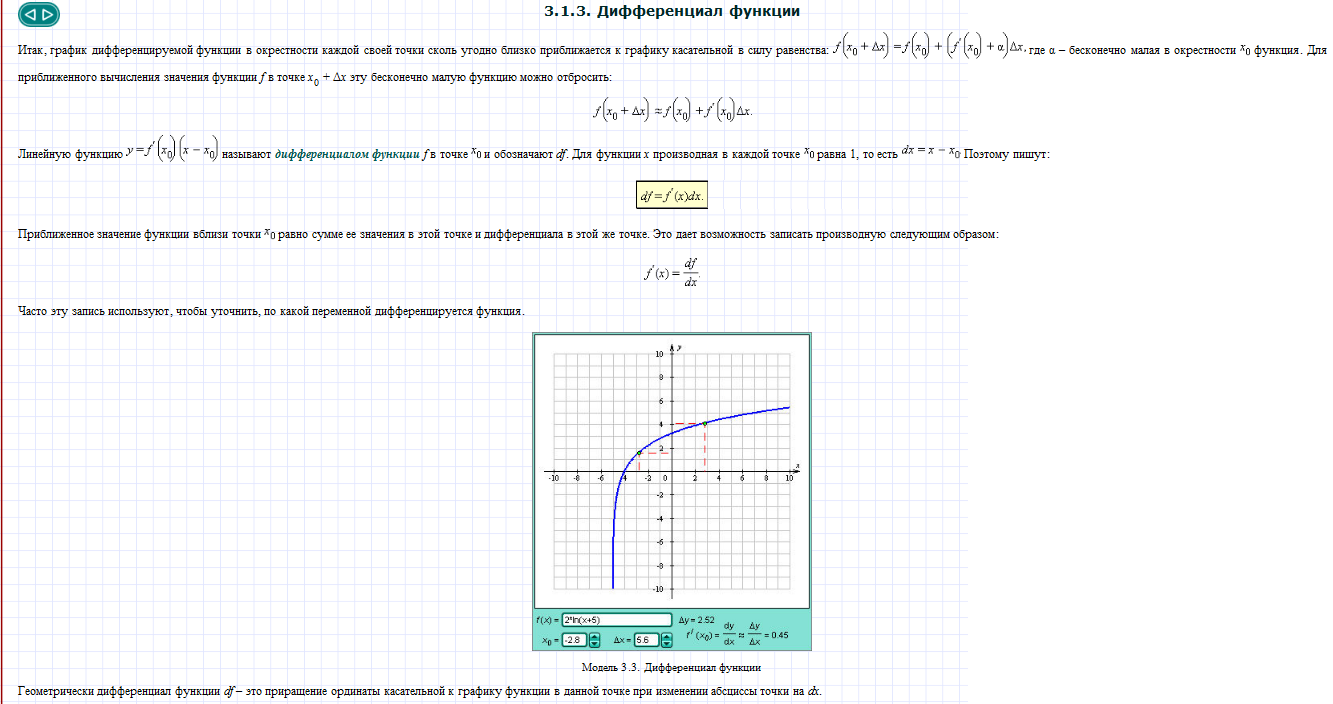
Предел функции. Таблица замечательных пределов.
Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел A в точке x0 если для всех значений x, достаточно близких к x0, значение f(x) близко к A.
Определение числового ряда.
Сумма числового ряда 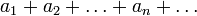 определяется как предел, к которому стремятся суммы первых nслагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится. Элементы ряда
определяется как предел, к которому стремятся суммы первых nслагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится. Элементы ряда 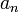 представляют собой либо вещественные, либо комплексные числа.
представляют собой либо вещественные, либо комплексные числа.
Определение
Пусть 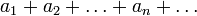 — числовой ряд. Число
— числовой ряд. Число 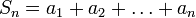 называется
называется 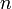 -ой частичной суммойряда
-ой частичной суммойряда 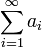 .
.
Сумма (числового) ряда — это предел частичных сумм 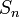 , если он существует и конечен. Таким образом, если существует число
, если он существует и конечен. Таким образом, если существует число 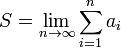 , то в этом случае пишут
, то в этом случае пишут 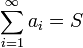 . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то говорят, что ряд расходится.
. Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то говорят, что ряд расходится.
Сходимость числовых рядов
Свойство 1. Если ряд
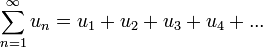 (1.1)
(1.1)
сходится и его сумма равна S, то ряд
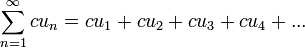 (1.2)
(1.2)
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится.
Свойство 2. Если сходится ряд (1.1) и сходится ряд
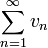 ,
,
а их суммы равны 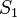 и
и 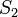 соответственно, то сходятся и ряды
соответственно, то сходятся и ряды
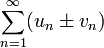 ,
,
причём сумма каждого равна соответственно 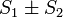 .
.
Необходимый признак сходимости ряда
Ряд 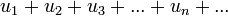 может сходиться лишь в том случае, когда член
может сходиться лишь в том случае, когда член 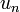 (общий член ряда) стремится к нулю:
(общий член ряда) стремится к нулю:
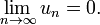
Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.
Признак Даламбера.
Признак Даламбера — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
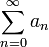
существует такое число 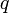 ,
, 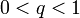 , что начиная с некоторого номера выполняется неравенство
, что начиная с некоторого номера выполняется неравенство
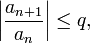
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
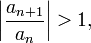
то ряд расходится.
Признак сходимости д’Аламбера в предельной форме
Если существует предел
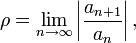
то рассматриваемый ряд абсолютно сходится если 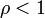 , а если
, а если 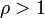 — расходится .
— расходится .
Замечание. Если 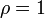 , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
, то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
Примеры
Ряд
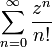
абсолютно сходится для всех комплексных 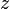 , так как
, так как
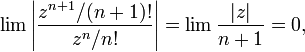
Ряд
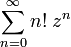
расходится при всех 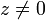 , так как
, так как
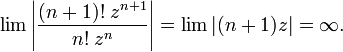
Если 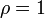 , то ряд может как сходиться, так и расходиться: оба ряда
, то ряд может как сходиться, так и расходиться: оба ряда
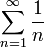 и
и 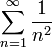
удовлетворяют этому условию, причём первый ряд расходится, а второй сходится.
38. Признак Коши.
Радикальный признак Коши — признак сходимости числового ряда:
Если для числового ряда 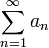 с неотрицательными членами существует такое число с неотрицательными членами существует такое число 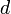 , , 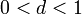 , что, начиная с некоторого номера, выполняется неравенство , что, начиная с некоторого номера, выполняется неравенство 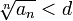 , то данный ряд сходится. , то данный ряд сходится. |
Предельная форма
Условие радикального признака равносильно следующему:
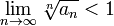
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
Если для ряда 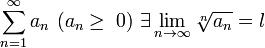 , то если , то если 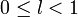 ряд сходится, если ряд сходится, если 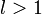 ряд расходится, если ряд расходится, если 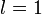 вопрос о сходимости ряда остается открытым. вопрос о сходимости ряда остается открытым. |
Доказательство
1. Пусть 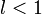 . Очевидно, что существует такое
. Очевидно, что существует такое 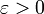 , что
, что 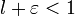 . Поскольку существует предел
. Поскольку существует предел 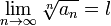 , то подставив в определение предела выбранное
, то подставив в определение предела выбранное  получим:
получим:
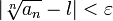
Раскрыв модуль, получаем:
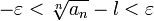
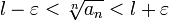
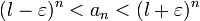
Поскольку 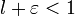 , то ряд
, то ряд 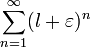 сходится. Следовательно, по признаку сравнения ряд
сходится. Следовательно, по признаку сравнения ряд 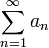 тоже сходится.
тоже сходится.
2. Пусть 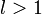 . Очевидно, что существует такое
. Очевидно, что существует такое 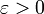 , что
, что 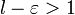 . Поскольку существует предел
. Поскольку существует предел 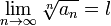 , то подставив в определение предела выбранное
, то подставив в определение предела выбранное  получим:
получим:
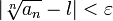
Раскрыв модуль, получаем:
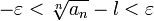
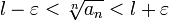
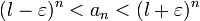
Поскольку 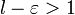 , то ряд
, то ряд 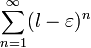 расходится. Следовательно, по признаку сравнения ряд
расходится. Следовательно, по признаку сравнения ряд 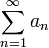 тоже расходится.
тоже расходится.
Примеры
1. Ряд
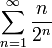
сходится, так как выполняется условие предельной формы радикального признака теоремы Коши
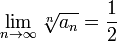
2. Рассмотрим ряд
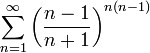
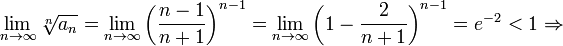 ряд сходится.
ряд сходится.
Сходимость степенного ряда.
Сходимость степенных рядов
Из формального степенного ряда с вещественными или комплексными коэффициентами путем приписывания формальной переменной 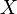 какого-нибудь значения в поле вещественных или комплексных чисел можно получить числовой ряд. Числовой ряд считается сходящимся (суммируемым), если сходится последовательность частичных сумм, составленных из его членов, и называется абсолютно сходящимся, если сходится последовательность частичных сумм, составленных из его членов, взятых по модулю (по норме).
какого-нибудь значения в поле вещественных или комплексных чисел можно получить числовой ряд. Числовой ряд считается сходящимся (суммируемым), если сходится последовательность частичных сумм, составленных из его членов, и называется абсолютно сходящимся, если сходится последовательность частичных сумм, составленных из его членов, взятых по модулю (по норме).
Признаки сходимости
Для степенных рядов есть несколько теорем, описывающих условия и характер их сходимости.
Первая теорема Абеля: Пусть ряд 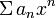 сходится в точке
сходится в точке 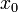 . Тогда этот ряд сходится абсолютно в круге
. Тогда этот ряд сходится абсолютно в круге 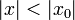 и равномерно по
и равномерно по 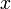 на любом компактном подмножестве этого круга.
на любом компактном подмножестве этого круга.
Обращая эту теорему, получаем, что если степенной ряд расходится при 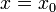 , он расходится при всех
, он расходится при всех 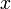 , таких что
, таких что 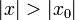 . Из первой теоремы Абеля также следует, что существует такой радиус круга
. Из первой теоремы Абеля также следует, что существует такой радиус круга 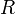 (возможно, нулевой или бесконечный), что при
(возможно, нулевой или бесконечный), что при 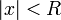 ряд сходится абсолютно (и равномерно по
ряд сходится абсолютно (и равномерно по 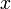 на компактных подмножествах круга
на компактных подмножествах круга 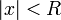 ), а при
), а при 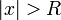 — расходится. Это значение
— расходится. Это значение 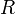 называется радиусом сходимости ряда, а круг
называется радиусом сходимости ряда, а круг 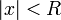 — кругом сходимости.
— кругом сходимости.
Формула Коши-Адамара: Значение радиуса сходимости степенного ряда может быть вычислено по формуле:
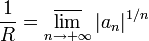
(По поводу определения верхнего предела 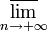 см. статью «Частичный предел последовательности».)
см. статью «Частичный предел последовательности».)
Пусть 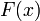 и
и 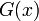 — два степенных ряда с радиусами сходимости
— два степенных ряда с радиусами сходимости 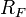 и
и 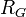 . Тогда
. Тогда
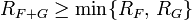
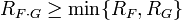
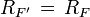
Если у ряда 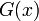 свободный член нулевой, тогда
свободный член нулевой, тогда
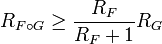
Вопрос о сходимости ряда в точках границы 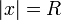 круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
круга сходимости достаточно сложен и общего ответа здесь нет. Вот некоторые из теорем о сходимости ряда в граничных точках круга сходимости:
Признак Д’Аламбера: Если при 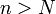 и
и 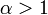 выполнено неравенство
выполнено неравенство
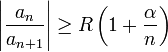
тогда степенной ряд 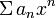 сходится во всех точках окружности
сходится во всех точках окружности 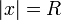 абсолютно и равномерно по
абсолютно и равномерно по 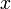 .
.
Признак Дирихле: Если все коэффициенты степенного ряда 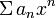 положительны и последовательность
положительны и последовательность 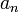 монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности
монотонно сходится к нулю, тогда этот ряд сходится во всех точках окружности 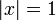 , кроме, быть может, точки
, кроме, быть может, точки 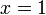 .
.
Вторая теорема Абеля: Пусть степенной ряд сходится в точке 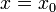 . Тогда он сходится равномерно по
. Тогда он сходится равномерно по 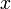 на отрезке, соединяющем точки 0 и
на отрезке, соединяющем точки 0 и 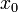 .
.
Сумма степенного ряда как функция комплексного параметра 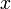 является предметом изучения теории аналитических функций.
является предметом изучения теории аналитических функций.
Умножение вектора на число.
Умножение вектора на число
Произведением ненулевого вектора а на число х =/= 0 называется вектор, длина которого равна | x | • | а |, а направление совпадает с направлением а, если х > 0, и противоположно ему, если х < 0.
Произведением нулевого вектора на любое число х и произведением любого вектора на число нуль называется нулевой вектор.
Произведение вектора а на число х обозначается х • а (числовой множитель пишется слева).
Согласно определению | x • а | = | x | • | а | для любого вектора а и любого числа х.
На рис. 18 изображены произведения вектора а на число х = 2 (вектор CD>) и на число х = —2 (вектор EF>).
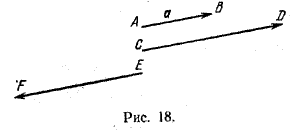
Умножение вектора на число обладает следующими свойствами:
1. Свойство ассоциативности (сочетательности):
х • (у • а) = (х • у) • а.
2. Свойство дистрибутивности (распределительности) относительно векторного множителя:
х • а + y • а = (х + у) • а.
3. Свойство дистрибутивности (распределительности) относительно числового множителя:
х • а + х • b = х • (a + b).
Если a = 0 или ху = 0, то равенство х(уа) = = (ху)а очевидно, так как слева и справа стоят нулевые векторы.
Пусть а =/= 0, ху =/= 0 и а = OA>. Тогда векторы х (у • OA>) и (ху) OA> лежат на прямой OA>, имеют длину |x| • |y| • |OA>| и направлены в одну сторону: в сторону вектора а = OA>, если ху > 0, и в противоположную сторону, если ху < 0. Таким образом, свойство 1 доказано.
Свойства 2 и 3 доказывать не будем. Заметим лишь, что свойства 1 и 2 являются свойствами векторов на прямой. Они уже доказывались в курсе геометрии восьмилетней школы. Свойство 3 является свойством векторов на плоскости; оно тоже было доказано.
Задача. В параллелограмме ABCD точка М есть точка пересечения диагоналей. Найти множитель k в каждом из следующих случаев:
1) M C> = k • CA>; 2) BD> = k • BM>; 3) AC> = k • CM>;
4) BB> = k • BD>; 5) AA> = k • CC>.
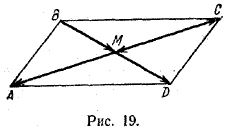
В соответствии с определением умножения вектора на число имеем (рис. 19)
1) M C> 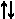 CA> , | CA| = 2•| MC |, откуда k = — 1/2;
CA> , | CA| = 2•| MC |, откуда k = — 1/2;
2) BM> 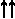 BD>, | BD | = 2 • | ВМ |, откуда k = 2;
BD>, | BD | = 2 • | ВМ |, откуда k = 2;
3) CM> 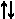 AC>, | CM | = 1/2• |AС |, откуда k = -2;
AC>, | CM | = 1/2• |AС |, откуда k = -2;
4) BB> = 0, BD> =/= 0, откуда k = 0;
5) AA> = 0, CC> = 0, откуда k — любое число.
Двойной интеграл.
Тогда двойной интеграл вычисляется по формуле
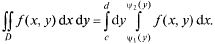
51. Вычисление двойного интеграла.
Комплексные числа , — расширение множества вещественных чисел, обычно обозначается 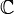 . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма 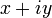 , где
, где 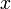 и
и 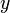 — вещественные числа,
— вещественные числа, 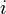 — мнимая единица[3].
— мнимая единица[3].
Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени 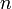 с комплексными коэффициентами имеет ровно
с комплексными коэффициентами имеет ровно 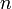 комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике,гидродинамике, картографии, квантовой механике, теории колебаний и многих других.
комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике,гидродинамике, картографии, квантовой механике, теории колебаний и многих других.
Алгебраическая форма:
Запись комплексного числа 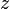 в виде
в виде 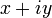 ,
, 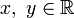 , называется алгебраической формой комплексного числа.
, называется алгебраической формой комплексного числа.
Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что 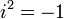 ):
):
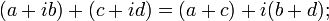
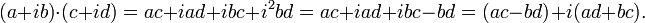
Схема испытаний Бернулли
Пусть один и тот же опыт повторяется п раз, испытания независимы, в результате каждого испытания может наступить или нет событие А. Пусть Р(А) = р — вероятность наступления А, тогда  = q = 1 - р. Такая схема испытаний называется схемой Бернулли. Найдем вероятность
= q = 1 - р. Такая схема испытаний называется схемой Бернулли. Найдем вероятность  того, что событие А произойдет при n испытаниях m раз.
того, что событие А произойдет при n испытаниях m раз.
Пространство элементарных событий состоит из произведений п событий А или  Событие
Событие
В, состоящее в том, что событие А произойдет при п испытаниях т раз, включает те  в которых А содержится
в которых А содержится  раз, их
раз, их  По формуле (34.7)
По формуле (34.7)  поэтому по (34.3)
поэтому по (34.3)

Формула  (34.10) называется формулой Бернулли.
(34.10) называется формулой Бернулли.
Пример: Найти вероятность того, что четырехзначный номер первого встречного автомобиля содержит две цифры 5.
Так как  = 4 (число цифр в номере),
= 4 (число цифр в номере),  = 2, событие А — данная цифра номера 5,
= 2, событие А — данная цифра номера 5,  — не 5, Р(А) = 1/10,
— не 5, Р(А) = 1/10,  = 9/10, то
= 9/10, то
 = 6 · 0,01· 0,81 = 0,0486
= 6 · 0,01· 0,81 = 0,0486
При больших значениях  подсчет
подсчет  проводится по при-
проводится по при-
ближенной формуле (локальная теорема Лапласа)

Если  велико, а
велико, а  то применяют приближенную
то применяют приближенную
формулу Пуассона:

65. Математическое ожидание дискретной величины, его свойства
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ [ mathematical expectation ]
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X) = x1 p1+ x2 p2+...+ xn pn.
Реально на основе данных выборки мы не можем вычислить M(X). Однако эту характеристику можно оценить. В качествеоценки можно использовать среднее арифметическое, то есть M(X) ≈`X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка. Математическое ожидание обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C.
2. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X).
3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z).
4. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(X×Y×Z) = M(X)×M(Y)×M(Z). Все эти свойства имеют большое практическое значение.
Математи́ческое ожида́ние — среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математическом сообществе Санкт-Петербурга обозначается через  (например, от англ. Expectedvalue или нем. Erwartungswert), в русской —
(например, от англ. Expectedvalue или нем. Erwartungswert), в русской —  (возможно, отангл. Meanvalue или нем. Mittelwert, а возможно от рус. Математическое ожидание). В статистике часто используют обозначение
(возможно, отангл. Meanvalue или нем. Mittelwert, а возможно от рус. Математическое ожидание). В статистике часто используют обозначение 
Определение
Пусть задано вероятностное пространство  и определённая на нём случайная величина
и определённая на нём случайная величина 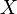 . То есть, по определению,
. То есть, по определению,  — измеримая функция. Если существуетинтеграл Лебега от
— измеримая функция. Если существуетинтеграл Лебега от 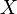 по пространству
по пространству  , то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается
, то он называется математическим ожиданием, или средним (ожидаемым) значением и обозначается  или
или  .
.

Дискретные распределения
Определение 3. Случайная величина называется простой или дискретной, если она принимает не более, чем счётное число значений. То есть  , где
, где  — разбиение
— разбиение  .
.
Распределение простой случайной величины тогда по определению задаётся:  . Введя обозначение
. Введя обозначение  , можно задать функцию
, можно задать функцию  . Очевидно, что
. Очевидно, что  . Используя счётную аддитивность
. Используя счётную аддитивность  , легко показать, что эта функция однозначно определяет распределение
, легко показать, что эта функция однозначно определяет распределение 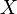 .
.
Определение 4. Функция  , где
, где  часто называется дискретным распределением.
часто называется дискретным распределением.
Пример 1. Пусть функция 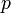 задана таким образом, что
задана таким образом, что  и
и  . Эта функция задаёт распределение случайной величины
. Эта функция задаёт распределение случайной величины 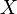 такой, что
такой, что  (распределение Бернулли).
(распределение Бернулли).
Теорема 3. Дискретное распределение обладает следующими свойствами:
1.  ;
;
2.  .
.
Свойства дисперсии
1)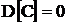 Дисперсия постоянной величины равна 0
Дисперсия постоянной величины равна 0
2) 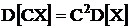 Постоянный множитель выносится за знак дисперсии с возведением в квадрат.
Постоянный множитель выносится за знак дисперсии с возведением в квадрат.
3) 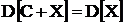 Дисперсия не изменяется, если к случайной величине прибавить или отнять случайное число.
Дисперсия не изменяется, если к случайной величине прибавить или отнять случайное число.
4) Если 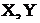 - независимые случайные величины, то дисперсия суммы равна сумме дисперсий. Дисперсия разности так же равна сумме дисперсий.
- независимые случайные величины, то дисперсия суммы равна сумме дисперсий. Дисперсия разности так же равна сумме дисперсий.
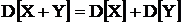 ;
;
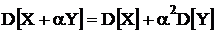 ;
;
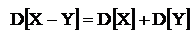 .
.
5) 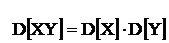 при
при 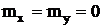 . Дисперсия произведения независимых случайных величин с нулевым математическим ожиданием равна произведению дисперсий.
. Дисперсия произведения независимых случайных величин с нулевым математическим ожиданием равна произведению дисперсий.
Полезное соотношение:
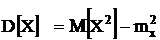 .
.
| Дисперсия случайной величины равна математическому ожиданию квадрата этой величины за вычетом квадрата математического ожидания. |
Доказательство:
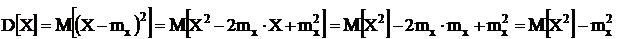 .
.
Приложение к лекции
-Проведем доказательство свойства 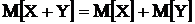 на примере дискретных случайных величин. В этом случае конкретные значения , которые может принимать случайная величинаZ=X+Y определяются выражением zij =( xi + yj), i = 1, 2, …, n; j = 1, 2, …, m
на примере дискретных случайных величин. В этом случае конкретные значения , которые может принимать случайная величинаZ=X+Y определяются выражением zij =( xi + yj), i = 1, 2, …, n; j = 1, 2, …, m
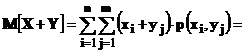
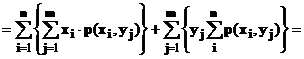
Положим, что появление значения yj это событие А и применим к этому событию формулуполной вероятности :
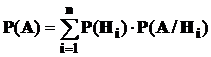 . *)
. *)
Событие А может появиться с одним из событий гипотез и отметим, что согласно теоремеумножения, которая была использована при выводе формулы *)
P(Hi)*P(A/Hi) = P(A*Hi)
События-гипотезы состоят в появлении значений х1, х2, . . .,хn. Тогда
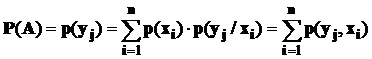 .
.
Следовательно, сумма вфигурных скобках второго слагаемого должна равняться вероятности появления yj - 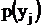 . Тогда можно написать:
. Тогда можно написать:
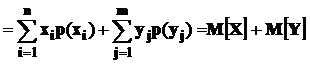
Доказательства других свойств матожидания
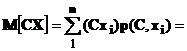
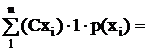
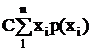
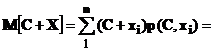
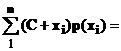
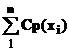 +
+ 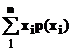
Доказательства свойства дисперсии 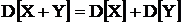
D[X+Y] =M[(X+Y-mx+y)2]=M[(X-mx+Y-my)2]= 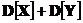 +2M[X-mx]*M[Y-my]
+2M[X-mx]*M[Y-my]
Возведение в степень приближенных чисел (ЧИСЛА 68 И 42 ЭТО ПРИМЕР. ВМЕСТО НИХ НАДО ПОДСТАВИТЬ ОДИНАКОВОЕ ЧИСЛО.)
Пусть требуется вычислить площадь прямоугольного участка, длина которого 68 м, а ширина — 42 м. Если бы числа 68 и 42 были точные, площадь участка в точности равнялась бы
68 * 42 = 2856 кв. м.
Но числа 68 и 42 не точные, а приближенные: в длине не ровно 68 м, а немного больше или меньше, так как невероятно, чтобы метр укладывался в ней в точности 68 раз. Да и самая длина метровой линейки едва ли в точности была равна 1 м. Мы можем, согласно предыдущему, выразить длину участка в метрах так:
68,?
Подобным же образом и ширину участка выразим через
42,?
Проделаем теперь умножение приближенных чисел:
68,? X 42,?
Выполнение действия видно из следующей схемы:
| Х | , | ? | |||
| , | ? | ||||
| ? | ? | ? | |||
| ? | |||||
| ? | |||||
| ?, | ? | ? |
Интерполяция
Интерполя́ция, интерполи́рование — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных экспериментальным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называетсяаппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить её значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Следует также упомянуть и совершенно другую разновидность математической интерполяции, известную под названием «интерполяция операторов». К классическим работам по интерполяции операторов относятся теорема Рисса-Торина (Riesz-Thorin theorem) и теорема Марцинкевича (Marcinkiewicz theorem), являющиеся основой для множества других работ.
Определения
Рассмотрим систему несовпадающих точек 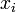 (
( 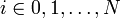 ) из некоторой области
) из некоторой области 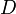 . Пусть значения функции
. Пусть значения функции 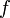 известны только в этих точках:
известны только в этих точках:
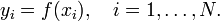
Задача интерполяции состоит в поиске такой функции 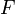 из заданного класса функций, что
из заданного класса функций, что
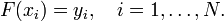
§ Точки 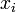 называют узлами интерполяции, а их совокупность — интерполяционной сеткой.
называют узлами интерполяции, а их совокупность — интерполяционной сеткой.
§ Пары 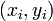 называют точками данных или базовыми точками.
называют точками данных или базовыми точками.
§ Разность между «соседними» значениями 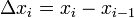 — шагом интерполяционной сетки. Он может быть как переменным так и постоянным.
— шагом интерполяционной сетки. Он может быть как переменным так и постоянным.
§ Функцию 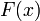 — интерполирующей функцией или интерполянтом.
— интерполирующей функцией или интерполянтом.
Пример
1. Пусть мы имеем табличную функцию, наподобие описанной ниже, которая для нескольких значений 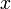 определяет соответствующие значения
определяет соответствующие значения 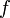 :
:
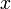 | 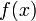 |
| 0,8415 | |
| 0,9093 | |
| 0,1411 | |
| −0,7568 | |
| −0,9589 | |
| −0,2794 |
Интерполяция помогает нам узнать какое значение может иметь такая функция в точке, отличной от указанных (например, при x = 2,5).
К настоящему времени существует множество различных способов интерполяции. Выбор наиболее подходящего алгоритма зависит от ответов на вопросы: как точен выбираемый метод, каковы затраты на его использование, насколько гладкой является интерполяционная функция, какого количества точек данных она требует и т. п.
2. Найти промежуточное значение (способом линейной интерполяции).
| 15.5 | |
| ? | |
| 19.2 |
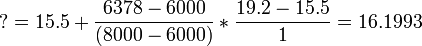
Преподаватель: Меркачева Л.И.
ЛИТЕРАТУРА:
- И.С. Пискунов «Дифференцированное и интегральное исчисление».
- Р.С. Гутер., П.Т. Резниковский «Программирование и вычислительная математика».
- В.П. Григорьев, Ю.А. Дубинский «Элементы высшей математики».
- Н.В. Богомолов «практическое занятие по математике».
Определение матрицы, элементы матрицы.
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные м
