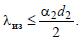Теплопередача через цилиндрическую стенку.

При теплопередаче с обоих сторон стенки имеют место ГУ-3. Для неограниченных стенок (l >> 10d) теплообменом с торцевых поверхностей пренебрегают и считают, что полный тепловой поток, отдаваемый горячим теплоносителем в стенку, равен тепловому потоку, проходящему через стенку и равен тепловому потоку, отдаваемому стенкой в холодный теплоноситель (см. рис. 2.15),

т.е. имеет место следующий тепловой баланс Qα1 = Qλ = Qα2 = Q. Запишем формулы, по которым можно рассчитать каждый из этих потоков: Qα1 = α1πd1l (tж1 – tс1);

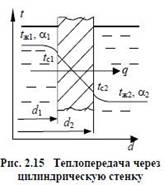
В итоге нами получена замкнутая система из трех уравнений, содержащая три неизвестных: Q, tc1 и tc2. Значения неизвестных найдем, не приводя систему к каноническому виду, а выразив из этих уравнений предварительно разницы температур:

и сложив почленно правые и левые части этих формул. Тогда получаем:

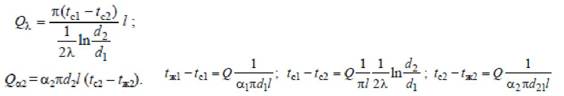
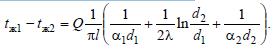
Отсюда находим

или, разделив на l, Выражения 1/(α1d1) и 1/(α2d2) называют термическими сопротивлениями теплоотдачи цилиндрических стенок. На практике очень часто встречаются такие стенки, у которых толщина во много раз меньше диаметра (тонкостенные цилиндры). У таких стенок можно считать, что d2/d1≈1, и тогда расчетная формула упрощается. Величину ln(d2/d1) разложим в ряд (при (d2/d1) < 2).

Поскольку для тонкостенных цилиндров (d2/d1) – 1 ≈ 0, то всеми

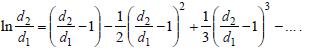
слагаемыми ряда, начиная со второго, можно

пренебрегать, как величинами более высоких порядков малости.

Значит:

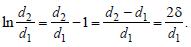
Учитывая

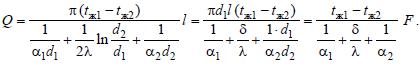
это, найдем теперь величину Q: Мы получили формулу, полностью совпадающую с расчетной формулой для плоской стенки.

Вывод: теплопередачу

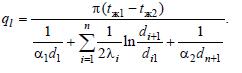
через тонкостенные трубы можно (и удобнее) рассчитывать по формуле плоской стенки. Обычно величину F берут для

горячей стороны стенки. Естественно, что для многослойной стенки суммируются термические сопротивления теплопроводности всех слоев:

Критический диаметр изоляции. Условие эффективной изоляции труб.

Оптимальная изоляция.

Чтобы уменьшить тепловые потери или создать безопасные условия труда, часто нагретые стенки покрывают слоем (или несколькими слоями) тепловой изоляции. Толщину изоляции определяют, учитывая задаваемые ограничения (например, q должно быть не более определенной величины, или t на поверхности изоляции не должна превышать заданного значения) или на основании технико-экономических расчетов оборудования. При теплоизоляции труб за счет слоя изоляции увеличивается термическое сопротивление теплопроводности, однако одновременно из-за увеличения наружного диаметра уменьшается термическое сопротивление внешней теплоотдачи. В результате теплопотери трубы могут не всегда уменьшаться. Чтобы лучше понять это, рассмотрим трубу с диаметрами d1 и d2, на которую нанесен слой тепловой изоляции толщиной δ (рис. 2.16). Общее термическое сопротивление такой двухслойной цилиндрической стенки найдется по формуле:

Изобразим теперь график зависимости

термических сопротивлений (отдельных слагаемых формулы (2.19)) при увеличении

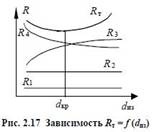
dиз = d2 + 2δ.Такие зависимости приведены на рис. 2.17.Первое и второе слагаемые не

содержат dиз и поэтому не меняются и изображаются некоторыми прямыми линиями. Третье

слагаемое с увеличением диаметра изоляции dиз увеличивается по логарифмическому

закону, а четвертое уменьшается гиперболически. При этом сумма Rт обязательно имеет

минимум. Поскольку ql = π (tж1 – tж2) / Rт, то понятно, что с увеличением dиз тепловые потери

qlмогут сначала и возрасти,и только затем уменьшаться.Диаметр изоляции,

соответствующий минимальному термическому сопротивлению (или максимальным

тепловым потерям) называют критическим, dкр. При dиз < dкр нанесение изоляции приводит к увеличению теплопотерь. Значит для эффективной работы изоляции необходимо, чтобы обязательно соблюдалось условие d2 ≥ dкр. В этом случае, как это видно из рис. 2.17, при нанесении изоляции всегда dиз = d2 + 2δ > dкр и реализуется правая ветвь кривой Rт = f (dиз). Величину dкр найдем, исследовав формулу (Rт) на экстремум. Для этого продифференцируем Rт по dиз и приравняем нулю полученное выражение:

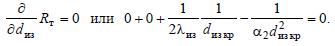
Теперь находим dкр = 2λиз / α2.

Как правило, величина α2 с изменением dиз практически не изменяется. Поэтому изменить dкр можно, лишь меняя материал изоляции (изменяя λиз). Объединяя формулы (2.20) и (2.21), найдем ограничение для λиз, гарантирующее эффективную работу изоляции:

В противном случае уменьшения теплопотерь тоже можно добиться существенным увеличением толщины изоляции, однако при этом большая часть слоя изоляции будет лежать, не принося пользы.

В последние годы в связи с динамичными изменениями цены тепла и материалов возрастает роль технико-экономических расчетов тепловой изоляции. Понятно, что с увеличением толщины изоляции тепловые потери (их стоимость Sт в рублях за весь период эксплуатации) уменьшаются, а стоимость материала изоляции Sм увеличивается. Рис. 2.18 иллюстрирует эти изменения. Поскольку слагаемые имеют противоположный характер изменения, то суммирующая кривая будет иметь минимум. Толщина слоя тепловой изоляции, соответствующая минимальной суммарной стоимости S, называется оптимальной толщиной δопт. В любом другом случае мы будем проигрывать либо за счет тепловых потерь, либо за счет увеличения стоимости материала изоляции. При расчетах многослойной изоляции можно ставить и решать вопрос об оптимальном сочетании толщин каждого слоя, поскольку эффективность и стоимость различных материалов различны. Доказано, например, что тот материал, у которого λиз меньше, следует располагать на горячей стороне стенки, там он работает более эффективно.