Элементы аналитической геометрии и линейной алгебры
1. Определители второго и третьего порядков. Основные свойства [1, приложение, §§1,3,4], [4, ч. 1, гл. 6, §§ 1,3,4].
2. Системы линейных уравнении. Метод Гаусса. Правило Крамера [1, приложение, §§1,2,5], [4, ч. 1, гл.6, §§ 2,5-7].
3. Трехмерное пространство. Векторы. Линейные операции над векторами [1, гл. 7, §§ 43 - 46, гл. 8, §§ 48-52], [4, ч. II, гл. 2, §§ 1-6].
4. Скалярное произведение векторов и его свойства. Выражение скалярного произведения через координаты векторов [1, гл. 9, §§ 53, 54], [4, ч. II, гл. 2, §§ 7-9].
5. Векторное и смешанное произведения векторов. Основные свойства. [1, гл. 10, §§ 55-58], [4, ч. II, гл. 2, §§ 11-15].
6. Уравнение плоскости и прямой в пространстве [1, гл. 12, §§ 63 – 67], [4, ч. II, гл. 4, §§ 1-10; гл. 5, §§1-7,9,10].
7. Уравнение прямой линии на плоскости [1, гл. 3, §11; гл. 4, §§16–20,.22], [4, ч.1, гл.3, §§1-10,12, 14-16].
8. Линии второго порядка. Эллипс, гипербола, парабола [1, гл. 5, §§ 24-26, 30-32, 35, 36], [4, ч. I, гл. 4, §§ 1 - 5].
9. Матрицы, действия над матрицами. Сложение матриц и умножение на число. Преобразование вектора с помощью матрицы. Обратная матрица. Решение систем линейных уравнений матричным методом [3, т.II, гл.21, §§2,4-9], [2, гл.3, §§ 12,13,16].
10. Собственные векторы и собственные значения матрицы. Квадратичные формы и их преобразования. Преобразование прямоугольных координат при переносе начала координат и повороте осей. Приведение общего уравнения линии второго порядка к каноническому виду [3, т. II, гл.21, §§11,14], [1, гл.2, § 10, гл.6, §41].
11. Ранг матрицы. Существование решений линейных уравнений. Теорема Кронекера-Капелли [3, т. II, гл. 21, §15].
Введение в математический анализ
12. Понятие функции одного действительного переменного. Способы задания функции. Четность, нечетность, периодичность. Основные элементарные функции и их графики [3, т. I, гл.1, §§ 6-9], [5, раздел 3, гл. 2, §§ I-4].
13. Предел переменной величины и предел функции. Основные теоремы о пределах. Первый замечательный предел. Число е [3, т. I, гл. 2, §§1-5,6-8], [5, раздел 3, гл. 2, §§1-4, 7-10].
14. Непрерывность функции. Свойства непрерывных функций [3, т. 1, гл. 2, §§9,10], [5, раздел 3, гл.2, §§12-16].
15. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых [3, т. I, гл. 2, §§ 4,11], [5, раздел 3, гл. 2, §§ 5,6].
Дифференциальное исчисление функций одной переменной
16. Производная функции, ее геометрический и механический смысл. Производная суммы, произведения, частного функций. Производные основных элементарных функций [3, т. I, гл.3, §§1-8,10,12], [5, раздел 4, гл. 1, §§ 1-7].
17. Производная сложной и обратной функций. Производные обратных тригонометрических функций. Таблица производных [3, т. I, гл. 3, §§ 9, 13-15], [5, раздел 4, гл. 1, §§ 8-10].
18. Дифференциал функции. Связь дифференциала с производной. Геометрический смысл дифференциала. Дифференциал суммы, произведения, частного функций [3, т. 1, гл. 3, §§ 20, 21], [5, раздел 4, гл. 1, §§ 11-13].
19. Производные и дифференциалы высших порядков. Формула Лейбница [3, т. I, гл. 3, §§ 22, 23], [5, раздел 4, гл. 1, § 14].
20. Теоремы Ролля и Лагранжа. Правило Лопиталя [3, т. I, гл. 4, §§ 1,2,4,5], [5, раздел 4, гл. 2, §§ 1,5].
21. Формула Тейлора с остаточным членом в форме Лагранжа. Представление функций 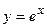 ,
, 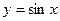 ,
, 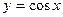 по формуле Тейлора [3, т. I, гл. 4, §§ 6,7].
по формуле Тейлора [3, т. I, гл. 4, §§ 6,7].
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
К КОНТРОЛЬНОЙ РАБОТЕ №1
1. Что называется определителем? Каковы свойства определителей и методы их вычисления? Что такое минор и алгебраическое дополнение?
2. Запишите в общем виде систему линейных уравнений. Какая система называется однородной, неоднородной? Напишите формулы Крамера. Когда применимы эти формулы?
3. Дайте определение геометрическим векторам, сложению и вычитанию векторов. Как определяются скалярное, векторное и смешанное произведения векторов? Как эти произведения выражаются через координаты векторов?
4. Напишите следующие уравнения плоскости: общее уравнение, нормальное уравнение, уравнение плоскости, проходящей через данную точку с заданной нормалью, уравнение плоскости в отрезках. Каковы условия параллельности и перпендикулярности плоскостей?
5. Напишите общие уравнения прямой в пространстве, канонические уравнения, уравнения прямой, проходящей через две точки. Каковы условия параллельности и перпендикулярности прямых? Запишите условия параллельности и перпендикулярности прямой и плоскости, условие их пересечения.
6. Напишите следующие уравнения прямой на плоскости: уравнение прямой с угловым коэффициентом, общее уравнение прямой, нормальное уравнение. Как найти угол между прямыми? Каковы условия параллельности и перпендикулярности прямых?
7. Дайте определение окружности, эллипса, гиперболы, параболы и напишите их канонические уравнения.
8. Начертите полярную систему координат и запишите формулы, связывающие прямоугольные и полярные координаты точки.
9. Дайте определение матрицы. Укажите, как они складываются. умножаются. Дайте определение обратной матрицы. Как найти обратную матрицу? Запишите систему линейных уравнений в матричной форме и объясните матричный метод ее решения.
10. Дайте определение функции. Что называется областью определения функции и каковы основные способы задания функции? Что называется графиком функции? Какие функции называются четными, нечетными, периодическими и каковы особенности их графиков?
11. Начертите графики основных элементарных функции. Сформулируйте определение предела функции при стремлении аргумента к конечному пределу и при стремлении аргумента к бесконечности.
12. Как связано понятие предела функции спонятиями ее пределовслева и справа?
13. Какая функция называется бесконечно малойи каковы ее основныесвойства?
14. Какая функция называетсябесконечно большой и какова ее связь с бесконечно малой?
15. Сформулируйте основные теоремы о пределах.
16. Что такое первый и второй замечательные пределы?
17. Сформулируйте определения непрерывности функции в точке и на отрезке. Какие точки называются точками разрыва функции?
18. Сформулируйте определение производной. Каков ее механический и геометрический смысл?
19. Запишите формулы производных суммы, произведения, частного двух функций и таблицу производных.
20. Сформулируйте правило дифференцирования сложной функции и теорему о дифференцировании обратной функции.
21. Что такое логарифмическое дифференцирование?
22. Как находятся производные функций, заданных параметрически?
23. Сформулируйте определение дифференциала функции. Каков его геометрический смысл?
24. Сформулируйте теоремы Ролля и Лагранжа. Каков их геометрический смысл?
25. В чем состоит правило Лопиталя для раскрытия неопределенностей?
КОНТРОЛЬНАЯ РАБОТА №1
Задача №1
Даны координаты вершин треугольника 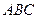 . Найти:
. Найти:
1) уравнения сторон 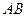 и
и 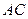 и их угловые
и их угловые
коэффициенты;
2) угол 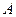 в радианах (градусах) с точностью до двух знаков после запятой;
в радианах (градусах) с точностью до двух знаков после запятой;
3) уравнение высоты 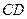 и ее длину;
и ее длину;
4) уравнение медианы 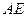 и координаты точки
и координаты точки 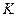 пересечения этой медианы с высотой
пересечения этой медианы с высотой 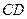 .
.
Сделать чертеж.
| Номер варианта | А | В | С |
| (2;5) | (14;-4) | (18;18) | |
| (0;3) | (12;-6) | (10;8) | |
| (-9;6) | (3;-3) | (7;19) | |
| (-12;-1) | (0;-10) | (4;12) | |
| (4;1) | (16;-8) | (14;6) | |
| (-3;10) | (9;1) | (7;15) | |
| (-1;4) | (11;-5) | (15;17) | |
| (3;6) | (15;-3) | (13;11) | |
| (-2;7) | (10;-2) | (8;12) | |
| (-6;8) | (6;-1) | (4;13) | |
| (-5;9) | (7;0) | (5;14) | |
| (-8;-3) | (4;-12) | (8;10) | |
| (-5;7) | (7;-2) | (11;20) | |
| (-4;10) | (8;1) | (12;23) | |
| (-7;4) | (5;-5) | (3;9) | |
| (0;2) | (12;-7) | (16;15) | |
| (-10;-9) | (2;0) | (6;22) | |
| (1;0) | (13;-9) | (17;13) | |
| (-4;12) | (8;3) | (6;17) | |
| (-10;5) | (2;-4) | (0;10) |
Задача №2
Даны координаты вершин пирамиды 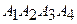 . Найти:
. Найти:
1) длину ребра 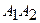 ;
;
2) угол между ребрами 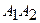 и
и 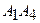 ;
;
3) уравнение плоскости 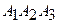 и угол между ребром
и угол между ребром
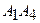 и плоскостью
и плоскостью 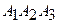 ;
;
4) уравнение высоты, опущенной из вершины 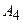 на грань
на грань
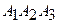 и ее длину;
и ее длину;
5) площадь грани 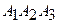 и объем пирамиды.
и объем пирамиды.
Сделать чертеж.
| Номер варианта | 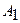 | 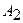 | 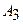 |  |
| (5;3;10) | (1;9;7) | (0;2;0) | (4;3;5) | |
| (2;3;5) | (5;3;7) | (4;2;10) | (1;2;7) | |
| (4;10;9) | (1;8;2) | (5;7;4) | (5;2;6) | |
| (2;5;8) | (1;4;9) | (2;1;6) | (5;4;2) | |
| (4;4;10) | (7;10;2) | (2;8;4) | (9;6;9) | |
| (2;3;9) | (3;3;6) | (2;1;7) | (1;2;5) | |
| (8;7;4) | (5;10;4) | (4;7;8) | (3;5;4) | |
| (2;6;5) | (1;2;5) | (4;0;6) | (6;4;8) | |
| (–2;8;2) | (6;8;9) | (5;3;3) | (7;10;3) | |
| (2;1;3) | (4;–1;1 ) | (1;0;–1) | (0;1;1) | |
| (0;2;7) | (1;5;0) | (0;7;1) | (4;2;5) | |
| (1;8;9) | (-1;3;0) | (4;7;8) | (2;4;9) | |
| (5;3;7) | (2;3;5) | (4;2;10) | (1;2;7) | |
| (8;6;4) | (2;1;1) | (5;6;8) | (8;10;7) | |
| (3;2;8) | (2;–1;7) | (6;3;1) | (2;–3;7) | |
| (5;3;1) | (2;3;7) | (7;2;2) | (5;7;7) | |
| (3;5;8) | (6;5;8) | (7;7;3) | (8;4;1) | |
| (–1;0;3) | (4;2;1) | (1;2;7) | (4;1;3) | |
| (6;9;4) | (7;5;9) | (4;6;5) | (1;5;5) | |
| (6;9;3) | (6;6;5) | (4;6;11) | (4;9;5) |
Задача №3
Сделать чертеж и составить уравнение линий:
1) расстояние каждой точки которой от начала координат и от точки 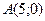 относятся как
относятся как 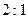 ;
;
2) расстояние каждой точки которой от точки 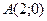 и от прямой
и от прямой 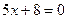 относятся как
относятся как 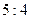 ;
;
3) расстояние каждой точки которой от точки 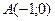 вдвое меньше расстояния ее от прямой
вдвое меньше расстояния ее от прямой 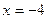 ;
;
4) для каждой точки которой расстояние от начала координат и от точки 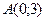 относятся друг к другу как
относятся друг к другу как 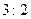 ;
;
5) каждая точка которой находится втрое дальше от точки 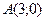 , чем от точки
, чем от точки 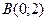 ;
;
6) расстояние каждой точки которой от точки 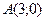 вдвое меньше расстояния ее от точки
вдвое меньше расстояния ее от точки 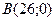 ;
;
7) для каждой точки которой расстояние от точки 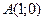 и от прямой
и от прямой 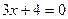 относятся как
относятся как 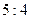 ;
;
8) каждая точка которой отстоит от точки 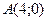 втрое дальше, чем от начала координат;
втрое дальше, чем от начала координат;
9) для каждой точки которой сумма квадратов расстояний до сторон квадрата с вершинами 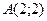 ,
, 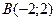 ,
, 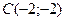 ,
, 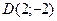 есть величина постоянная, равная
есть величина постоянная, равная 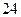 ;
;
10) каждая точка которой одинаково удалена от точки 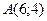 и от прямой
и от прямой 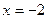 ;
;
11) каждая точка которой одинаково удалена от точки 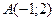 и от оси
и от оси 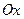 .
.
12) для каждой точки которой сумма квадратов расстояний до точек 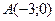 и
и 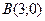 равна
равна 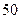 ;
;
13) для каждой точки которой сумма квадратов расстояний до точек 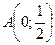 и
и 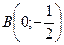 равна
равна 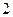 ;
;
14) расстояние каждой точки которой от точки 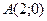 и от прямой
и от прямой 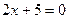 относятся как
относятся как 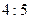 ;
;
15) расстояние каждой точки которой от точки 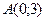 втрое больше расстояния от точки
втрое больше расстояния от точки 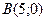 ;
;
16) каждая точка которой равноудалена от точки 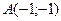 и от прямой
и от прямой 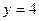 ;
;
17) для каждой точки которой отношение расстояния до точки 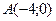 к расстоянию до прямой
к расстоянию до прямой 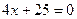 равно
равно 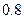 ;
;
18) каждая точка которой одинакова удалена от точки 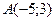 и от начала координат;
и от начала координат;
19) каждая точка которой находится вдвое дальше от точки 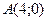 , чем от точки
, чем от точки 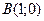 ;
;
20) полученной при таком движении точки 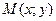 , что расстояние от нее до точки
, что расстояние от нее до точки 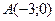 вдвое меньше расстояния от точки
вдвое меньше расстояния от точки  ;
;
Задача №4
Решить систему линейных уравнений методом Гаусса.
1. 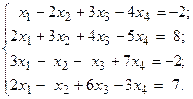 2.
2. 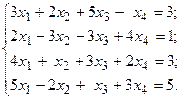
3. 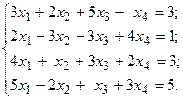 4.
4. 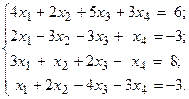
5. 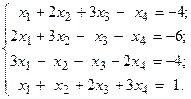 6.
6. 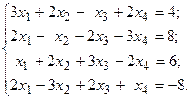
7. 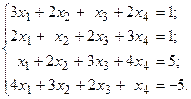 8.
8. 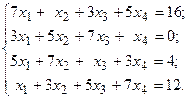
9. 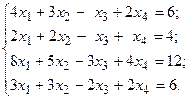 10.
10. 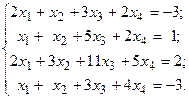
11. 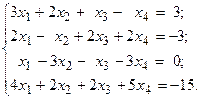 12.
12. 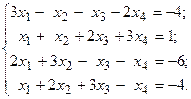
13. 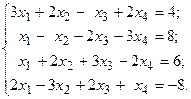 14.
14. 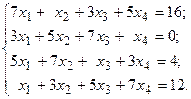
15. 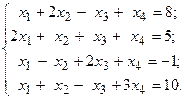 16.
16. 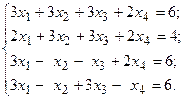
17. 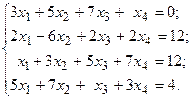 18.
18. 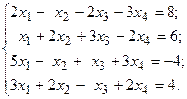
19. 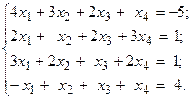 20.
20. 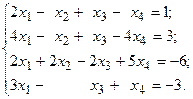
Задача №5
Решить систему линейных уравнений двумя способами:
1) методом Крамера;
2) используя обратную матрицу.
1. 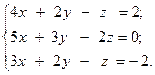 2.
2. 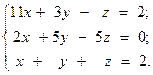
3. 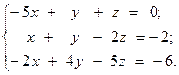 4.
4. 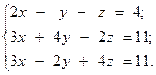
5. 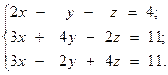 6.
6. 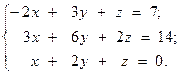
7. 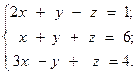 8.
8. 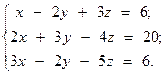
9. 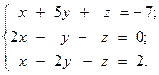 10.
10. 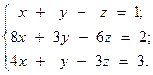
11. 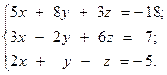 12.
12. 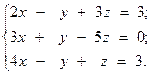
13. 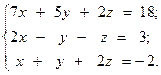 14.
14. 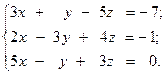
15. 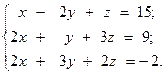 16.
16. 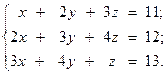
17. 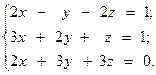 18.
18. 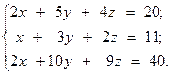
19. 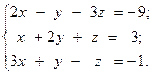 20.
20. 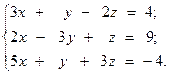
Задача №6
Вычислить пределы, не пользуясь правилом Лопиталя.
1. a) 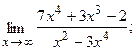 б)
б) 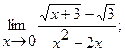
в) 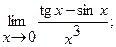 г)
г) 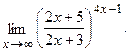
2. a) 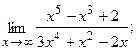 б)
б) 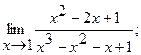
в) 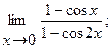 г)
г) 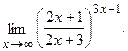
3. a) 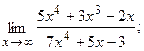 б)
б) 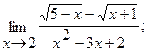
в) 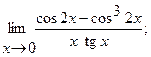 г)
г) 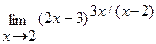 .
.
4. a) 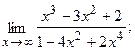 б)
б) 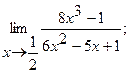
в) 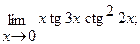 г)
г) 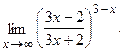
5. а) 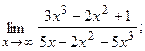 б)
б) 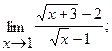
в) 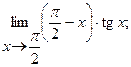 г)
г) 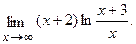
6. а) 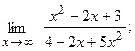 б)
б) 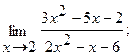
в) 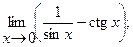 г)
г) 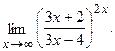
7.а)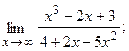 б)
б) 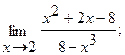
в) 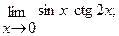 г)
г) 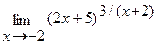 .
.
8. а) 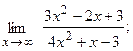 б)
б) 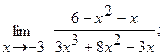
в) 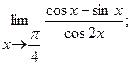 г)
г) 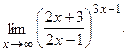
9. а) 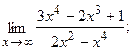 б)
б) 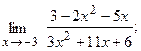
в) 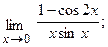 г)
г) 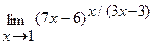 .
.
10. а) 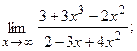 б)
б) 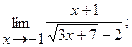
в) 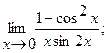 г)
г) 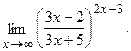
11.a) 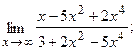 б)
б) 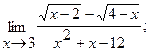
в) 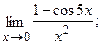 г)
г) 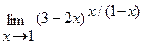
12.а) 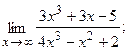 б)
б) 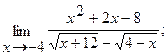
в) 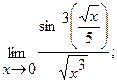 г)
г) 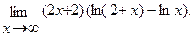
13.а) 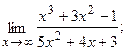 б)
б) 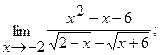
в) 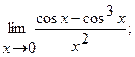 г)
г) 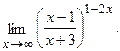
14.a) 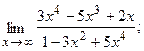 б)
б) 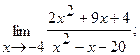
в) 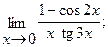 г)
г) 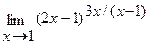 .
.
15.а) 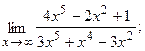 б)
б) 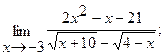
в) 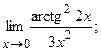 г)
г) 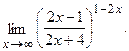
16. а) 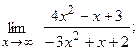 б)
б) 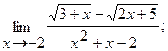
в) 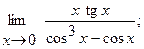 г)
г) 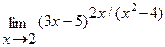 .
.
17.а)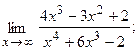 б)
б) 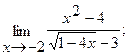
в) 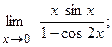 г)
г) 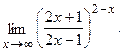
18. а) 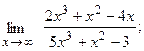 б)
б) 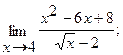
в) 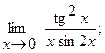 г)
г) 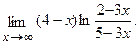
19. а) 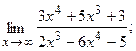 б)
б) 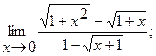
в) 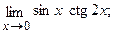 г)
г) 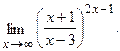
20. а) 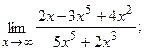 б)
б) 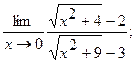
в) 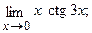 г)
г) 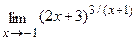 .
.
Задача №7
Исследовать функцию 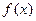 на непрерывность. Определить характер точек разрыва, если они существуют. Сделать чертеж.
на непрерывность. Определить характер точек разрыва, если они существуют. Сделать чертеж.
1. 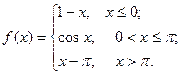 2.
2. 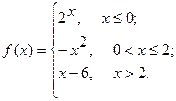
3. 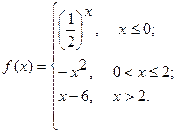 4.
4. 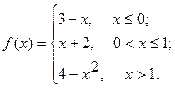
5. 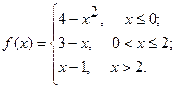 6.
6. 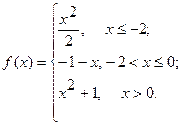
7. 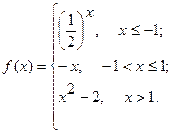 8.
8. 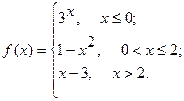
9. 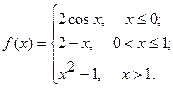 10.
10. 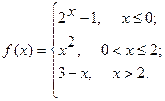
11. 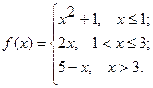 12.
12. 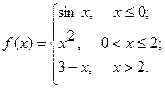
13. 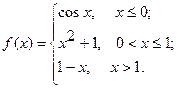 14.
14. 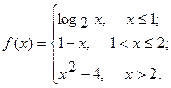
15. 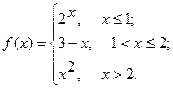 16.
16. 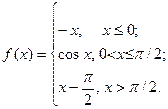
17. 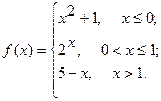 18.
18. 
19. 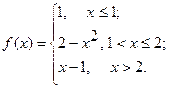 20.
20. 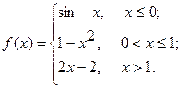
Задача №8
Найти производные заданных функций
1.a) 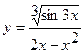 ; б)
; б) 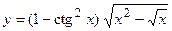 ;
;
в) 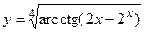 ; г)
; г) 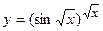 ;
;
д) 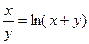 ; е)
; е) 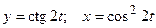 .
.
2. a) 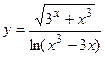 ; б)
; б) 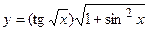 ;
;
в) 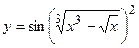 ; г)
; г) 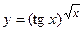 ;
;
д) 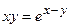 ; е)
; е) 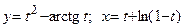 .
.
3. a) 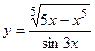 ; б)
; б) 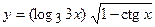 ;
;
в) 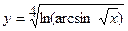 ; г)
; г) 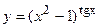 ;
;
д) 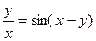 ; е)
; е) 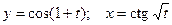 .
.
4. а) 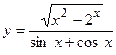 ; б)
; б) 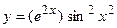 ;
;
в) 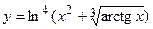 ; г)
; г) 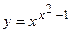 ;
;
д) 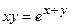 ; е)
; е) 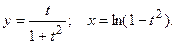
5. a) 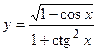 ; б)
; б) 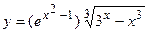 ;
;
в) 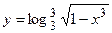 ; г)
; г) 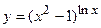 ;
;
д) 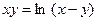 ; е)
; е) 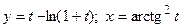 .
.
6. а) 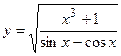 ; б)
; б) 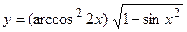 ;
;
в) 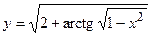 ; г)
; г) 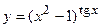 ;
;
д) 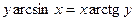 ; е)
; е) 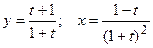 .
.
7. a) 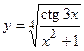 ; б)
; б) 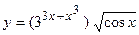 ;
;
в) 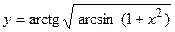 ; г)
; г) 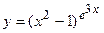 ;
;
д) 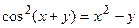 ; е)
; е) 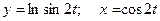 .
.
8. а) 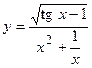 ; б)
; б) 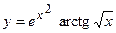 ;
;
в) 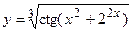 ; г)
; г) 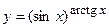 ;
;
д) 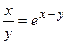 ; е)
; е) 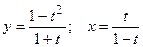 .
.
9. а) 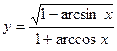 ; б)
; б) 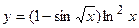 ;
;
в) 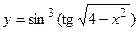 ; г)
; г) 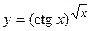 ;
;
д) 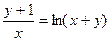 ; е)
; е) 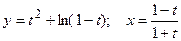 .
.
10. а) 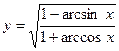 ; б)
; б) 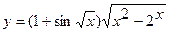 ;
;
в) 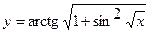 ; г)
; г) 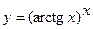 ;
;
д) 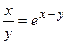 ; е)
; е) 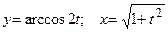 .
.
11. а) 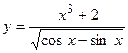 ; б)
; б) 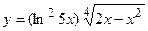 ;
;
в) 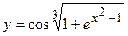 ; г)
; г) 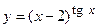 ;
;
д) 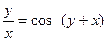 ; е)
; е) 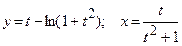 .
.
12. a) 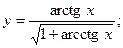 б)
б) 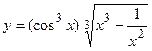 ;
;
в) 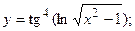 ; г)
; г) 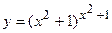 ;
;
д) 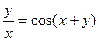 ; е)
; е) 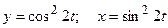 .
.
13. a) 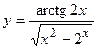 ; б)
; б) 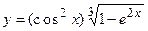 ;
;
в) 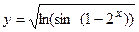 ; г)
; г) 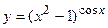 ;
;
д) 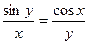 ; е)
; е) 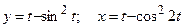 .
.
14. а) 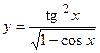 ; б)
; б) 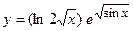 ;
;
в) 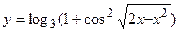 ; г)
; г) 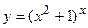 ;
;
д) 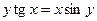 ; е)
; е) 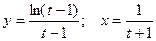 .
.
15. a) 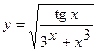 ; б)
; б) 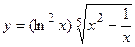 ;
;
в) 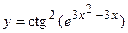 ; г)
; г) 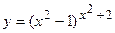 ;
;
д) 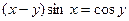 ; е)
; е) 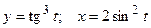 .
.
16. a) 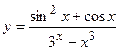 ; б)
; б) 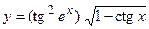
в) 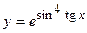 ; г)
; г) 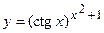 ;
;
д) 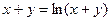 ; е)
; е) 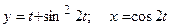 .
.
17. а) 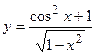 ; б)
; б) 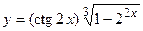 ;
;
в) 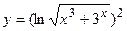 ; г)
; г) 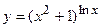 ;
;
д) 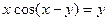 ; е)
; е) 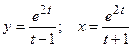 .
.
18. a) 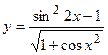 ; б)
; б) 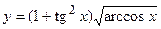 ;
;
в) 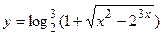 ; г)
; г) 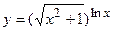 ;
;
д) 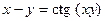 ; е)
; е) 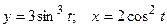 .
.
19. а) 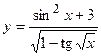 ; б)
; б) 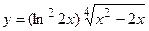 ;
;
в) 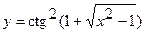 ; г)
; г) 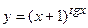 ;
;
д) 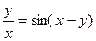 ; е)
; е) 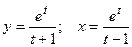 .
.
20. а) 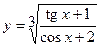 ; б)
; б) 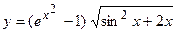 ;
;
в) 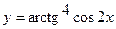 ; г)
; г) 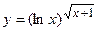 ;
;
д) 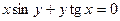 ; е)
; е) 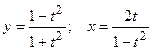 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ К КОНТРОЛЬНОЙ РАБОТЕ №1
Задача №1
Даны координаты вершин треугольника 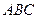 :
: 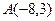 ,
, 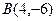 ,
, 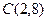 . Найти:
. Найти:
1) уравнения сторон 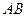 и
и 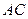 и их угловые
и их угловые
коэффициенты;
2) угол 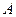 в радианах (градусах) с точностью до двух знаков после запятой;
в радианах (градусах) с точностью до двух знаков после запятой;
3) уравнение высоты 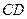 и ее длину;
и ее длину;
4) уравнение медианы 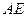 и координаты точки
и координаты точки 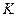 пересечения этой медианы с высотой
пересечения этой медианы с высотой 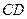 .
.
 Сделать чертеж (рис.1).
Сделать чертеж (рис.1).
Рис. 1
Решение. 1) Найдем координаты векторов 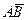 и
и 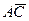 , для чего воспользуемся формулой
, для чего воспользуемся формулой
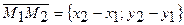 .
.
Тогда 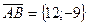 ,
, 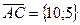 . Эти векторы являются направляющими векторами прямых, на которых лежат соответствующие стороны треугольника и для получения их уравнений можно использовать каноническое уравнение прямой на плоскости
. Эти векторы являются направляющими векторами прямых, на которых лежат соответствующие стороны треугольника и для получения их уравнений можно использовать каноническое уравнение прямой на плоскости
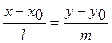 .
.
В результате получим
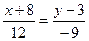 (
( 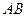 ),
),
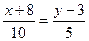 (
( 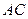 ).
).
Разрешая эти уравнения относительно 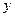 , т.е. приводя их к виду уравнения прямой с угловым коэффициентом
, т.е. приводя их к виду уравнения прямой с угловым коэффициентом
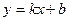 ,
,
найдем 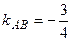 ,
, 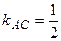 .
.
2) Угол 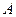 треугольника совпадает с углом между векторами
треугольника совпадает с углом между векторами 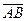 и
и 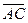 и для его нахождения можно использовать формулу
и для его нахождения можно использовать формулу
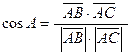 ,
,
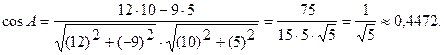 По таблице найдем значение угла
По таблице найдем значение угла 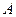 : <
: < 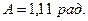 (
( 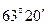 ).
).
3) Для получения уравнения высоты 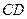 приведем уравнение стороны
приведем уравнение стороны 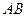 к виду общего уравнения прямой на плоскости
к виду общего уравнения прямой на плоскости
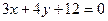 (
( 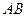 ).
).
Из рисунка видно, что вектор нормали к прямой 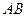 является направляющим вектором высоты
является направляющим вектором высоты 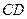 , т.е.
, т.е. 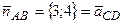 , и можно вновь воспользоваться каноническим уравнением прямой на плоскости
, и можно вновь воспользоваться каноническим уравнением прямой на плоскости
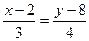 (
( 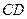 ).
).
Длину высоты 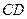 вычислим по формуле вычисления расстояния от точки
вычислим по формуле вычисления расстояния от точки 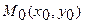 до прямой
до прямой 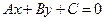 :
:
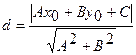 .
.
В нашем случае 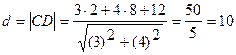 .
.
4) Найдем координаты точки 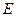 , являющейся серединой отрезка
, являющейся серединой отрезка 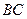
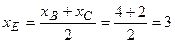 ;
; 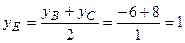 .
.
Т.о., 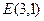 , и для нахождения уравнения медианы
, и для нахождения уравнения медианы 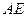 можно использовать уравнение прямой, проходящей через две точки
можно использовать уравнение прямой, проходящей через две точки 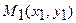 и
и 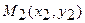 :
: 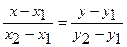 . Тогда получим
. Тогда получим
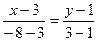 или
или 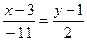 (
( 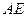 ).
).
Наконец, для вычисления координат точки 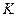 , решим совместно уравнения прямых
, решим совместно уравнения прямых 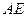 и
и 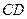 , предварительно приведя их уравнения к общему виду
, предварительно приведя их уравнения к общему виду
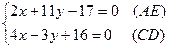 .
.
Отсюда получим 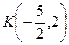 .
.
Задача №2
Даны координаты вершин пирамиды 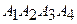 :
:
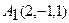 ,
,
