Аппроксимация функции с помощью MathCAD

Вводим исходные данные (рис.12).

Рис.12. Фрагмент листа MathCAD с исходными данными

Линейная регрессия

Линейная регрессия в системе MathCAD выполняется по векторам аргумента Х и отсчетов Y функциями:

intercept(X,Y) – вычисляем параметр 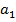, смещение линии регресси по вертикали;

slope(X,Y)– вычисляем параметр 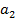, угловой коэффициент линии регрессии.

Полученные значения коэффициентов используем в уравнение регрессии .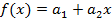

Функция Corr(Y,y(x)) – вычисляет коэффициент корреляции Пирсона. Чем он ближе к 1, тем точнее обрабатываемые данные соответствуют линейной зависимости [3].

Вычислив параметры линейной регрессии, строим графики исходной функции y и функции линейной регрессии f(x) (рис.13)

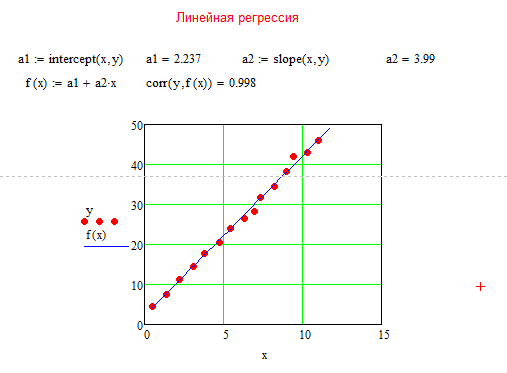
Рис. 13. Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии тренда для линейной аппроксимации

Уравнение линейной регрессии, полученное в MathCAD: y=2.237+3.99.

Полиномиальная регрессия

Одномерная полиномиальная регрессия с произвольной степенью n полинома и с произвольными координатами отсчетов в MathCAD выполняется функцией regress(X,Y,n), которая вычисляет вектор S, в составе которого находятся коэффициенты 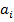полинома n-й степени.

Значения коэффициентов 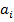могут быть извлечены из вектора S функцией submatrix(S, 3, length(S)-1, 0, 0).

Полученные значения коэффициентов используем в уравнении регрессии .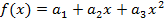

Вычислив параметры квадратичной регрессии, строим графики исходной функции y и функции квадратичной регрессии f(x) (рис. 14).

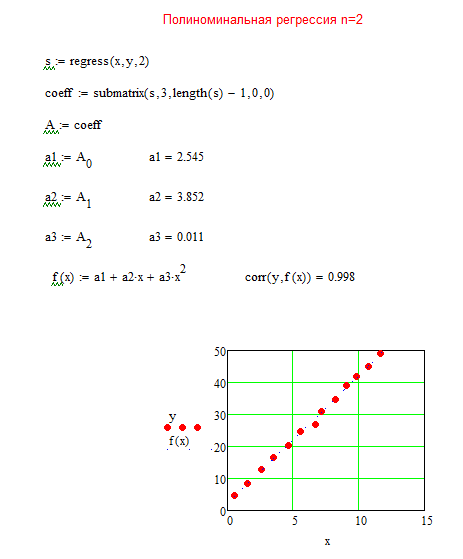
Рис.14. Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии для квадратичной аппроксимации

Уравнение полиномиальной регрессии : y=2.545+3.852х+0.011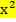

Экспоненциальная регрессия

Для определения экспоненциальной функции решим систему (10) в MathCAD:

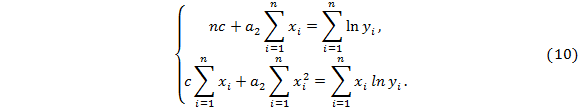
Для этого с помощью значков суммирования векторов и векторизации , находящихся на панели векторов и матриц, вычисляем: 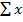, , 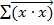, 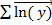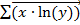(рис.15).

Затем составляем матрицы А и В из соответствующих коэффициентов системы линейных уравнений (10) и находим решение системы с помощью встроенной функции lsolve (см. рис. 15).

Решив систему (10), получим значения коэффициентов с и .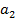

Коэффициент 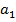вычисляем по формуле: 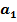=exp(с).

Полученные значения коэффициентов используем в уравнение регрессии .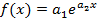

Вычислив параметры экспоненциальной регрессии, строим графики исходной функции y и функции экспоненциальной регрессии f(x) (рис. 15).

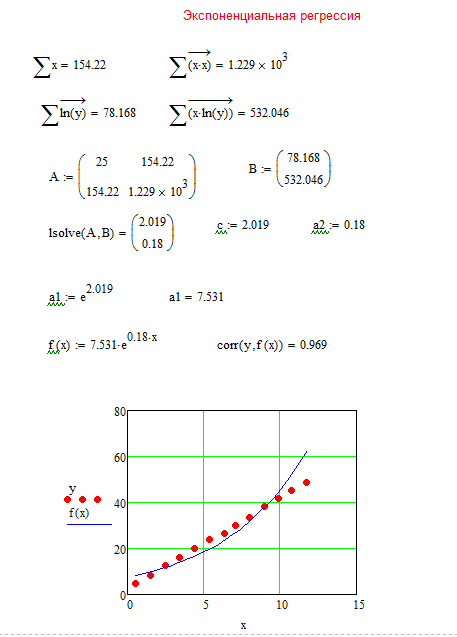
Рис. 15. Фрагмент листа MathCAD с найденными коэффициентами для системы уравнений и графиком зависимости линии для экспоненциальной аппроксимации

Уравнение экспоненциальной регрессии: .

Проведенные расчеты показывают, что результаты, полученные с помощью среды MathCAD, полностью совпадают со значениями, рассчитанными в MS Excel.

Заключение

Сделаем заключение по результатам полученных данных:

1. В ходе обработки исходных данных средствами функций MS Excel и MathCAD были получены три варианта уравнения аппроксимации: линейная, квадратичная и экспоненциальная.

2. Анализ результатов расчетов показывает, что линейная аппроксимация наилучшим образом описывает экспериментальные данные, так как имеет самый высокий коэффициент детерминированности (0,9960).

Уравнение линейной аппроксимации имеет следующий вид: y=2.237+3.99

3. Совпадение значений величин, полученных на графиках и рассчитанных по формулам в MS Excel, говорит о правильности вычислений.

4. Результаты, полученные с помощью среды MathCAD, полностью совпадают со значениями, рассчитанными в MS Excel. Это говорит о верности вычислений.

Список использованной литературы

1. Бердышев В.И., Петрак Л.В. Аппроксимация функций, сжатие численной информации, приложения. – Екатеринбург: УрО РАН, 1999. – 296 с.

2. Малинина Л.А. Основы информатики: Учебник для вузов. – Ростов н/Д.: Феникс, 2006. – 352 с.

3. Макаров Е.Г. MathCAD: Учебный курс. – СПб.: Питер, 2009. – 384 с.