Решение иррациональных уравнений

Определение: Иррациональным уравнением называется уравнение, в котором неизвестное находится под знаком корня.

Правило: Для решения иррационального уравнения 2 степени необходимо возвести в квадрат обе части уравнения. В заключении необходимо выполнить проверку.

Формулы сокращенного умножения

квадрат суммы: ( а + в )² = а² + 2ав + в²

квадрат разности: ( а - в )² = а² - 2ав + в²

разность квадратов: а² - в² = ( а - в )( а + в)

куб суммы: ( а + в )³ = а³ + 3а² в + 3ав² + в³

куб разности: ( а - в )³ = а³ - 3а² в + 3ав² - в³

разность кубов: а³ - в³ = ( а – в)( а² + ав + в² )

сумма кубов: а³ + в³ = ( а + в)( а² - ав + в² )

Решение систем уравнений с двумя неизвестными

Правило: Для решения системы двух уравнений с двумя неизвестными, необходимо из одного уравнения системы выразить одно неизвестное через другое, а затем подставить полученное выражение в другое уравнение системы. Ответ записывается в виде (х;у).

2. Примеры и упражнения

Пример 1:Решить иррациональное уравнение

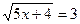
Решение:

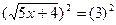
5х+4=9

5х=9-4

5х=5

х=1

Проверка:

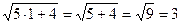
3=3

Ответ: х=1

Пример 2:Решить иррациональное уравнение

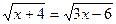
Решение:

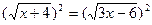
х+4=3х-6

х-3х=-6-4

-2х=-10

х=5

Проверка:

а)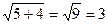

б)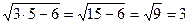

3=3

Ответ: х=5

Пример 4:Решить иррациональное уравнение

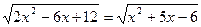
Решение:

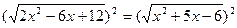
2х²-6х+12=х²+5х-6

2х²-6х+12-х²-5х+6=0

х²-11х+18=0

а=1, b=-11, с=18

х_{1,2= = =}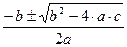

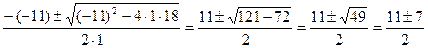
х₁= 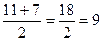х₂=

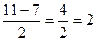
Проверка:

1) х₁=9

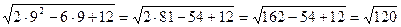
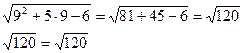
2) х₂=2

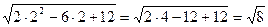
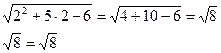
Ответ: х₁=9, х₂=2

Пример 5:Решить иррациональное уравнение

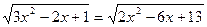
Решение:

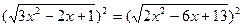
3х²-2х+1=2х²-6х+13

3х²-2х+1-2х²+6х-13=0

х²+4х-12=0

а=1, b=4, с=-12

х_{1,2= = =}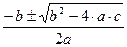

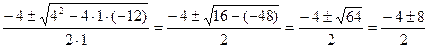
х₁= 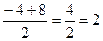х₂=

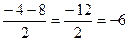
Проверка:

3) х₁=2

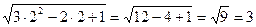
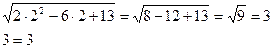
4) х₂=-6

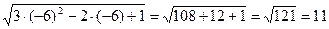
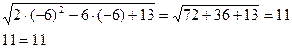
Ответ: х₁=2, х₂=-6

Пример 6:Решить иррациональное уравнение

х-6 =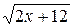

Решение:

(х-6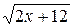)² =( )²

(х)²-2·х·6+6²=2х+12

х²-12х+36=2х+12

х²-12х+36-2х-12=0

х²-14х+24=0

а=1, b=-14, с=24

х_{1,2= =} =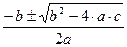

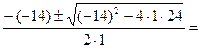
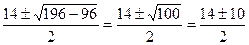
х₁= 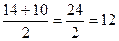х₂=

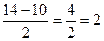
Проверка:1) х₁=12

12-6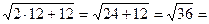=6

6

6=6

2) х₂=2- не уд

2-6 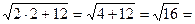=-4

4

-4≠4

Ответ: х=12

Пример 7:Решить иррациональное уравнение

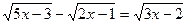
Решение:

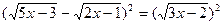
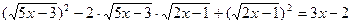
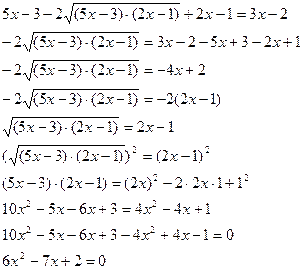
а=6, b=-7, с=2

х_1,2= =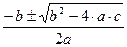

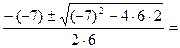
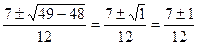
х₁= 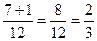х₂=

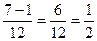
Проверка:

1) х₁=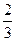

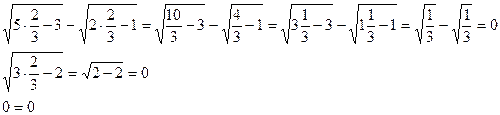
2) х₂= - не уд

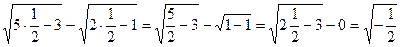( по определению 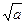,а≥0)

Ответ:х=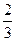

Пример 3:Решить иррациональное уравнение

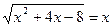
Решение:

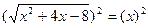
х²+4х-8=х²

х²+4х-8-х²=0

4х-8=0

4х=0+8

4х=8

х=2

Проверка:

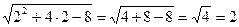
х=2

2=2 Ответ: х=2

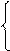Пример 8: Решить систему уравнений:

х+у=5

х·у=6

Решение:

х+у=5 х·у=6

Выразим х через у и подставим во 2 уравнение:

х=5-у, (5-у)·у=6

5у-у² –6=0

-у²+5у-6=0 : (-1)

у²-5у+6=0

а=1,b=-5, с=6

у_{1,2= -=} =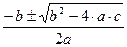

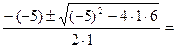
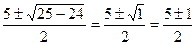
у₁= 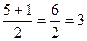у₂=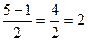

у₁=3 у₂=2

х₁=5-у=5-3=2 х₂= 5-у =5-2=3

Ответ: (2;3), (3;2)

Пример 9: Решить систему уравнений:

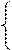х²-у²=200

х+у=20

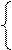Решение:

(х-у)·(х+у)=200

х+у=20 (разделим первое уравнение системы на второе уравнение)

,

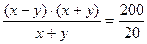получим: х-у=10

х=10+у, (подставим во второе уравнение системы)

(10+у)+у=20

2у=20-10

2у=10

у=5,

х=10+у=10+5=15

Ответ: (15;5)

Пример10: Решить систему уравнений:

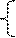х+х·у+у=-1

х-х·у+у=3

Решение:

Сложим первое и второе уравнение системы:

(х+х·у+у)+( х+х·у+у)=-1+3

х+у+х+у=2

2х+2у=2

2(х+у)=2

х+у=1,

х=1-у

Подставим выражение для х в первое уравнение системы:

(1-у)+(1-у)·у+у=-1

1-у+у-у²+у=-1

-у²+у+1+1=0

-у²+у+2=0

у²-у-2=0

а=1,b=-1, с=-2

у_{1,2= =} =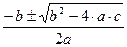

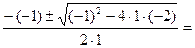
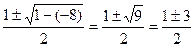
у₁= 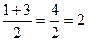у₂=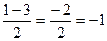

у₁=2 у₂=-1

х₁=1-у=1-2=-1 х₂= 1-у =1-(-1)=2

Ответ: (-1;2), (2;-1)

Варианты контрольной работы

Задание 1: Решить иррациональное уравнение

Вариант 1:

1)

2)

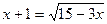
3)

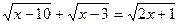
Вариант 2:

1)

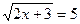
2)

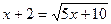
3)

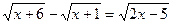
Вариант 3:

1)

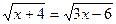
2)

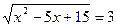
3)

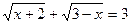
Вариант 4:

1)

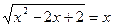
2)

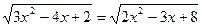
3)

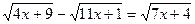
Вариант 5:

1)

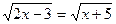
2)

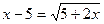
3)

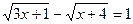
Вариант 6:

1)

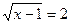
2)

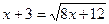
3)

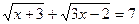
Вариант 7:

1)

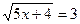
2)

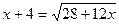
3)

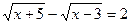
Вариант 8:

1)

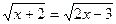
2)

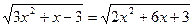
3)

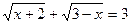
Вариант 9:

1)

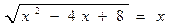
2)

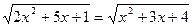
3)

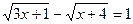
Вариант 10:

1)

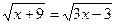
2)

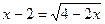
3)

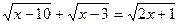
Вариант 11:

1) 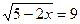2)

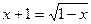
3)

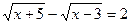
Вариант 12:

4)

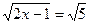
5)

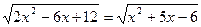
6)

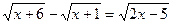
Вариант 13:

1)

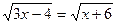
2)

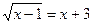
3)

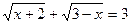
Вариант14:

1)

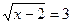
2)

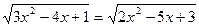
3)

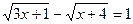
Вариант 15:

1)

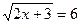
2)

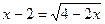
3)

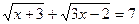
Вариант 16:

1)

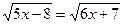
2)

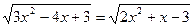
3)

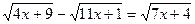
Вариант 17:

1) 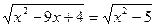2)

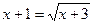
3)

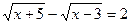
Вариант 18:

1)

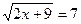
2)

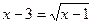
3)

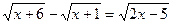
Вариант19:

1)

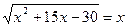
2)

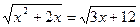
3)

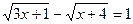
Вариант 20:

1)

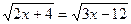
2)

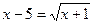
3)

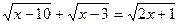
Вариант 21:

1)

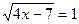
2)

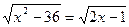
3)

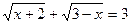
Вариант 22:

1)

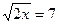
2)

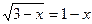
3)

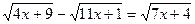
Вариант 23:

1) 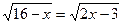2)

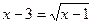
3)

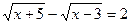
Вариант 24:

1) 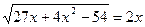2)

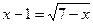
3)

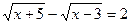
Вариант 25:

1) 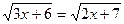2)

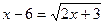
3)

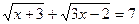
Вариант 26:

1) 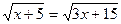2)

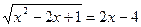
3)

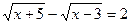
Вариант 27:

1) 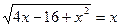2)

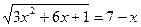
3)

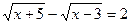
Вариант 28:

1) 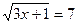2)

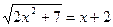
3)

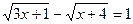
Вариант 29:

1) 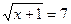2)

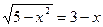
3)

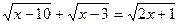
Вариант 30:

1)

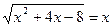
2)

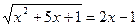
3)

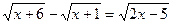
Задание 2: Решить систему уравнений

Вариант 1:	х-у=3 х·у=10
Вариант 2:	х-у=4 х·у=5
Вариант 3:	х2-у2=27 х+у=-3
Вариант 4:	х-у=-3 х·у=4
Вариант 5:	х-х·у+у=7 х+х·у+у=5
Вариант 6:	х-у=-2 х·у=3
Вариант 7:	х2-у2=9 х-у=1
Вариант 8:	х-у=9 х·у=10
Вариант 9:	х2-у2=207 х-у=9
Вариант 10:	х-у=7 х·у=-6
Вариант 11:	х-у=-9 х·у=-20
Вариант 12:	х-х·у+у=-7 х+х·у+у=1
Вариант 13:	х+у=7 х·у=-18
Вариант 14:	х-у=10 х·у=-24
Вариант 15:	х2-у2=207 х-у=9
Вариант 16:	х+у=5 х·у=6
Вариант 17:	х+у=-4 х·у=-12
Вариант18:	х+у=1 х·у=-6
Вариант 19:	х2-у2=153 х+у=17
Вариант 20:	х2-у2=9 х-у=1
Вариант 21:	х-х·у+у=-7 х+х·у+у=1
Вариант 22:	х+у=2 х·у=-8
Вариант 23:	х-у=4 х·у=-3
Вариант 24:	х-у=-3 х·у=4
Вариант 25:	х-у=8 х·у=-7
Вариант 26:	х-у=2 х·у=8
Вариант 27:	х2-у2=153 х+у=17
Вариант 28:	х-у=0 х·у=1
Вариант 29:	х-у=1 х·у=6
Вариант 30:	х+у=5 х·у=6

Содержание темы «Тригонометрические функции»

Радианная мера угла. Поворот точки вокруг начала координат

Определение угла в один радиан, формулы перевода градусной меры в радианную и наоборот. Понятие «единичная окружность», поворот точки вокруг начала координат.

Определение тригонометрических функций

Определения тригонометрических функций sinα, cosα, tgα,ctgα. Таблица значений тригонометрических функций

Знаки тригонометрических функций Значения sinα, cosα, tgα,ctgα в различных четвертях. Определение знака числа sina, cosa и tg a при заданном значении a

Зависимость между тригонометрическими функциями одного и того же аргумента

Основное тригонометрическое тождество, зависимость между тангенсом и котангенсом, зависимость между тангенсом и косинусом, зависимость между котангенсом и синусом

Четность и нечетность тригонометрических функций. Периодичность тригонометрических функций Область определения и область значений, тождества четности и периодичности для синуса и косинуса, свойства четности функций y=tgx и y=ctgx и периодичности

Формулы сложения, приведения

Формулы сложения. Значения тригонометрических функций углов, больших 90°, сводятся к значениям для острых углов; правила записи формул приведения

Тригонометрические функции двойного, половинного аргумента

Формулы двойного угла, Формулы половин-ного угла синуса, косинуса и тангенса;Формулы, выражающие sina, cosa и tg a через tg (a/2)

Преобразование суммы и разности тригонометрических функций в произведение

Формулы суммы и разности.Формулы сложения.Формулы двойного угла

Функция у = sinх, её свойства и график Определения синусоиды и линии синусов, построение графиков указанных функций и выполнение с ними простейших преобразований.

Функция у = cosх, её свойства и график

Определения косинусоиды и линии косинусов, построение графиков указанных функций и выполнение с ними простейших преобразований. Функции у = tgх, у = ctgх, их свойства и графики Определения тангенсоиды, построение графиков указанных функций и выполнение с ними простейших преобразований.

Основные сведения из теории