Построение амплитудно-частотной, фазово-частотной и

Амплитудной фазово-частотной характеристики усилительного

(пропорционального, безынерционного) звена САУ

Цель работы:

Ознакомиться с режимами работы объекта управления и его динамическими

Характеристиками.

Научится рассчитывать и графически представлять динамические

Характеристики типового звена САУ.

Порядок выполнения работы:

Ознакомиться с описанием «Практической работы».

В усилительном звене выходная величина в каждый момент времени пропорциональна входной величине: .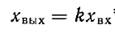

Коэффициент про­порциональности k на­зывается коэффициентом усиления или коэффи­циентом передачизвена.

Уравнение усили­тельного звена алгебраическое. Это свидетельствует о том, что усилительное звено передает сигнал мгновенно, без динамических переходных процессов и иска­жений.

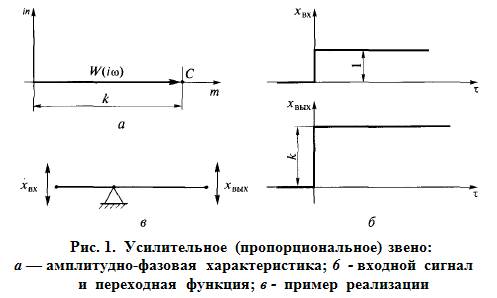
На рис. 1 представлен характер изменения по времени выходной величины усилительного звена при подаче на его вход постоянной величины Х_вх .

Передаточная функция усилительного звена имеет вид:

W(p) = k

Примеры усилительных

звеньев:

-рычажные передачи;

-механические редукторы;

-меха­нические пружины;

-усилители электронные;

-делители напряжения;

-датчики сиг­налов.

Механические пружины (рис. 2) широко применяют в качестве важнейших и нагруженных деталей почти в любой современной машине. Особо важную роль выполняют они в транспортных машинах, двигателях внутреннего сгорания, в часах и приборах. Всякая пружина или рессора является механическим аккумулятором энергии. Воспринимая внешнее усилие, пружина или рессора сжимается (прогибается), запасаясь энергией упругой деформации. Как только внешняя сила прекращает свое действие, упругие силы разжимают пружину, производя при этом необходимую работу за счет энергии, запасенной во время сжатия. Как и при всяком механическом преобразовании энергии, происходит некоторая потеря энергии, главным образом, на трение и нагревание.

а— цилиндрическая винтовая пружина растяжения

с закрытой (плотной) навивкой;

б— цилиндрическая винтовая пружина сжатия,

навитая из проволоки круглого сечения;

в— цилиндрическая винтовая пружина сжатия,

навитая из прутка прямоугольного сечения;

г —цилиндрическая винтовая пружина сжатия,

навитая из многожильного троса;

д— коническая винтовая пружина сжатия;

е —параболоидная пружина сжатия, навитая из

плющенной проволоки;

ж —телескопическая пружина, навитая из полосы

или ленты прямоугольного сечения;

з — матрацная пружина с криволинейной

характеристикой (прогрессивно-

возрастающей);

и — призматическая пружина сжатия, навитая на

прямоугольную оправку;

к, л — цилиндрические винтовые пружины

кручения;

м — плоская спиральная пружина:

н — тарельчатая пружина;

о — кольцевая пружина.

По конструктивным особенностям пружины подразделяются на следующие группы:

а) пружины растяжения (рис.2, а);

б) пружины сжатия (рис.2, 6, и);

в) пружины кручения (рис.2, к, л);

г) пружины специальные (рис.2, м, н, о).

Аналитическое выражение вектора АФЧХусилительного звена

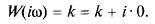
Поскольку АФЧХ усилительного звена не зависит от из­менения частоты ώ, годограф ее вектора (рис. 1, а) превраща­ется в точку С, находящуюся на действительной положительной полуоси комплексной плоскости на расстоянии kот начала ко­ординат. Пропорциональное звено мгновенно (без инерции) реагирует на возмущающее воздействие. По переходной функции, показан­ной на рис. 1,б, видно, что выходной сигнал этого звена про­порционален входному сигналу и ордината выходного сигнала равна коэффициенту пропорциональности k. Примером реализации пропорционального звена может слу­жить жесткий стержень, лежащий на опоре (рис. 1, в), при пе­ремещении одного конца которого Х_вхмгновенно перемещается другой его конец Х_вых .

Для исследования типового динамического звена или объекта управления (ОУ) в ТАУ используется метод математического моделирования. При этом ОУ рассматривается как простой преобразователь входного сигнала в выходной без учета физико-химической сущности процесса, протекающего в нем, т.е. целью исследования ОУ является формирование его математической модели — уравнения взаимосвязи выходного сигнала объекта (регулируемого параметра) с входным сигналом. Объект управления может работать в 2-х режимах: статиче­ском и динамическом.

При статическом режимеприток энергии или вещества в объект равен оттоку и объект находится в состоянии равновесия.

При динамическом режименарушено равновесие между прито­ком и оттоком энергии или вещества.

Математическая модель ОУ или уравнение математической взаимосвязи его выходного и входного сигналов в динамическом режиме работы называется динамической характеристикой.

Для определения динамических характеристик звена на его вход пода­ется одно из 3-х типовых возмущающих воздействий (рис. 3):

1) единичный скачок (рис. 3, а);

2) единичный импульс (рис. 3, б);

3) синусоидальные колебания с различными частотой ώ или периодомТ(рис. 3, в).

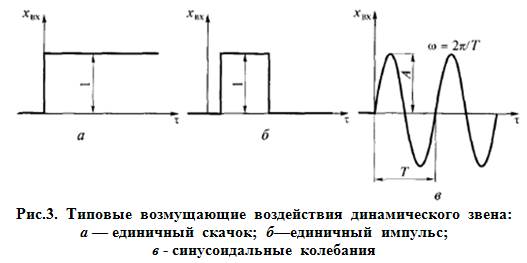
На практике чаще всего используют возмущающее воздействие в виде единичного скачка. Реакция объекта на это возмущение (график изменения во времени выходного сигнала объекта после подачи его на вход возмущения в виде единичного скачка) назы­вается переходной (временной) характеристикой.

Определения:

1. Передаточной функциейназывается преобразованное по Лапла­су исходное дифференциальное уравнение, т.е. уравнение, запи­санное в виде отношения преобразованных по Лапласу выходного и входного сигналов звена (ОУ).

В преобразовании по Лапласу исходное дифференциальное уравнение называется оригиналом,а преобразованное и записан­ное в операторной форме уравнение — его изображением.Суть преобразования Лапласа заключается в замене функций вещественных переменных Х_вых (t) и Х_вх (t) на функции комплексных переменных Х_вых (p) и Х_вх (p), где р— оператор Лапласа (комплексное число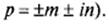

2. Амплитудной частотной(или амплитудно-частотной) характеристикой (АЧХ) называется зависимость отношения амплитуды выходных колебаний к амплитуде входных колебаний А_вых / А_вхот частоты колебаний ώ и обозначается А (ώ).

3.Фазовой частотной (или фазово-частотной) характеристикой (ФЧХ) зависимость фазового сдвига φмежду выходными и входными колебаниями от частоты ώи обозначается φ (ώ).

4.Ампли­тудной фазово-частотной характеристикой системы (АФЧХ) называется отношение выходной величины системы к входной величине_, выраженное в комплексной форме и обозначается W (jώ).

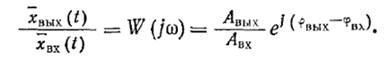
Амплитудно-фазовая частотная характеристика строится на комплексной плоскости и представляет собой годограф частотной передаточной функциипри изменении частоты ώот 0 до ∞. То есть АФЧХ - это траектория, описываемая на комплексной плоскости концом радиуса-вектора, модуль и аргумент которого соответственно равны А (ώ)и φ (ώ), при изменении частоты ώот 0 до ∞.

АФЧХ системы не зави­сит от времени. В этом ее принципиальное отличие от вре­менной характеристики. Если временная характеристика определяет поведение системы в переходном процессе, то АФЧХ выражает зависимость параметров установившихся выходных колебаний от тех же параметров входных колебаний при различных частотах.