Тема 1. теоретические основы и методология
КОНСПЕКТ ЛЕКЦИЙ
И ЗАДАНИЯ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
Для обучающихся
по направлению подготовки магистров
Нефтегазовое дело»
Составитель: к. с. н., доцент Дружинина И.В.
Ó Федеральное государственное бюджетное образовательное
учреждение высшего образования «Тюменский индустриальный университет», 2017 г.
ТЕМА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ И МЕТОДОЛОГИЯ
СТАТИСТИКИ
Термин «статистика» (от латинского слова «status» – состояние, определенное положение вещей) в настоящее время употребляется в основном в трех значениях:
1) ОТРАСЛЬ ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ, направленная на сбор, обработку и анализ данных, характеризующих социально-экономическое развитие страны, ее регионов, отраслей экономики, отдельных предприятий;
2) ОТРАСЛЬ ОБЩЕСТВЕННЫХ НАУК, занимающаяся разработкой теоретических положений и методов, которые используются статистической практикой;
как наука, статистика – это еще и УЧЕНИЕ О СИСТЕМЕ ПОКАЗАТЕЛЕЙ, дающих всестороннее представление об общественных явлениях, о народном хозяйстве в целом и отдельных его отраслях; - это ИНСТРУМЕНТ ПОЗНАНИЯ, используемый в различных науках для установления специфических закономерностей, которые действуют в конкретных массовых явлениях, изучаемых данной наукой;
3) СИНОНИМ СЛОВА "ДАННЫЕ", т.е. числовые (или цифровые) данные, характеризующие различные стороны жизни государства: политические отношения, культуру, население, производство, торговлю и т.д.
Как наука статистика имеет свой предмет и специфические методы исследования.
· ПРЕДМЕТ СТАТИСТИКИ - количественная сторона качественно определённых массовых социально-экономических явлений и процессов, их структура и распределение, размещение в пространстве, движение во времени. Статистика также выявляет действующие количественные зависимости, тенденции и закономерности развития явлений, причём в конкретных условиях места и времени.
Теоретическую основу статистикисоставляют следующие важнейшие категории: совокупность; вариация; признак; закономерность.
· СТАТИСТИЧЕСКАЯ СОВОКУПНОСТЬ - объект статистического исследования (в каждом конкретном случае), т.е. множество единиц, обладающих массовостью, качественной однородностью и наличием вариации. Например, множества промышленных предприятий, семей, студентов, граждан какой-либо страны.
· Каждый отдельно взятый элемент данного множества называется ЕДИНИЦЕЙ СОВОКУПНОСТИ.
Единицы совокупности обладают определёнными свойствами, качествами.
· Свойство, качество единицы совокупности, отличающее её от других единиц, называется ПРИЗНАКОМ.
Признаки различаются способами их измерения, характером выражения, вариации и другими особенностями, влияющими на приёмы статистического изучения (табл. 1).
· Под КАЧЕСТВЕННОЙ ОДНОРОДНОСТЬЮ СТАТИСТИЧЕСКОЙ СОВОКУПНОСТИ понимается сходство единиц по каким-либо существенным признакам (т.е. определяющим главное содержание изучаемого явления), но различие по каким-либо другим.
Например, качественная однородность множества студентов заключается в принадлежности этих лиц к определённой социальной группе.
Таблица 1 - КЛАССИФИКАЦИЯ ПРИЗНАКОВ В СТАТИСТИКЕ
| Основание классификации | Виды признаков |
| 1. По характеру выражения признаков | 1. Описательные (атрибутивные): а) номинальные; б) порядковые 2. Количественные |
| 2. По способу измерения (учёта) | 1. Первичные (учитываемые) 2. Вторичные (расчётные) |
| 3. По отношению ко времени | 1. Моментные 2. Интервальные |
| 4. По характеру вариации | 1. Альтернативные 2. Дискретные 3. Непрерывные |
| 5. По содержательности | 1. Существенные 2. Несущественные |
| 6. По причинности | 1. Факторные 2. Результативные |
· ВАРИАЦИЯ ПРИЗНАКОВ - различие величины того или иного признака у разных единиц совокупности - обусловлена различным сочетанием условий, в которых развиваются или существуют единицы совокупности. Именно наличие вариации предопределяет необходимость статистики.
Вариация признаков отражается статистическим распределением, которое имеет большое практическое и научное значение.
Важнейшей категорией статистики является статистическая закономерность.
· СТАТИСТИЧЕСКАЯ ЗАКОНОМЕРНОСТЬ – это количественная закономерность изменения в пространстве и во времени массовых явлений и процессов общественной жизни, состоящих из множества элементов (единиц совокупности).
Важнейшая особенность статистической закономерности (главное ее отличие от других видов закономерностей) заключается в том, что она свойственна не отдельным единицам совокупности, а всей их массе (совокупности в целом) и проявляется только при достаточно большом числе наблюдений и только в среднем.
Это обусловливает её взаимосвязь с ЗАКОНОМ БОЛЬШИХ ЧИСЕЛ, основное содержание которого заключается в том, что в сводных статистических характеристиках действия элементов случайности взаимопогашаются, хотя они и могут проявляться в индивидуальных признаках единиц статистической совокупности.
Предмет статистики имеет ряд особенностей:
1) исследуются не отдельные факты, а массовые социально-экономические явления и процессы (т.е. множества отдельных фактов, обладающих как индивидуальными, так и общими признаками);
2) статистика изучает, прежде всего, количественную сторону общественных явлений и процессов в конкретных условиях места и времени; количественную характеристику статистика выражает через определённого рода числа - СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ[1];
3) статистика характеризует структуру общественных явлений, т.е. их внутреннее строение, при этом выявляются составные части социально-экономических явлений, эти составные части сопоставляются с явлением в целом и между собой, данная структура сравнивается с другими однотипными структурами, а также с заданной (нормативной или плановой) и выявляются причины отклонений;
4) изменения уровня явления и его структуры исследуются во времени, при этом анализ динамики включает: установление уровня явления на определённые моменты или промежутки времени и среднего уровня, выявление характера изменений за каждый промежуток времени и в целом, определение величины и темпов изменения, установление основной тенденции изменений, их закономерности и составление статистического прогноза.
5) выявление связей; явления общественной жизни взаимосвязаны и взаимообусловлены: изменение одних явлений предопределяет другие; наибольшее значение имеет выявление причинно-следственных связей для того, чтобы воздействовать на общественные явления с целью их изменения в интересах общества; с помощью специальной методологии статистика определяет количественные связи между общественными явлениями.
Для изучения своего предмета статистика разрабатывает и применяет разнообразные МЕТОДЫ, совокупность которых образует СТАТИСТИЧЕСКУЮ МЕТОДОЛОГИЮ. Применение в статистическом исследовании конкретных методов обусловлено поставленными при этом задачами и зависит от характера исходной информации.
Всё многообразие статистических методов систематизируется по их целевому применению в трёх стадиях экономико-статистического исследования, выполняемых последовательно: 1) сбор первичной информации; 2) статистическая сводка и обработка первичной информации; 3) анализ статистической информации.
На начальной стадии статистического исследования применяется МЕТОД МАССОВОГО СТАТИСТИЧЕСКОГО НАБЛЮДЕНИЯ.
Важнейшим методом второй стадии является МЕТОД СТАТИСТИЧЕСКОЙ СВОДКИ И ГРУППИРОВКИ. Одним из этапов процесса группировки является построение РЯДОВ РАСПРЕДЕЛЕНИЯ, т.е. распределение единиц наблюдения по величине или значению признака. Результаты статистической сводки и группировки оформляются в виде СТАТИСТИЧЕСКИХ ТАБЛИЦ.
Для третьей стадии статистического исследования характерны:
- МЕТОД ОБОБЩАЮЩИХ СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ (включает применение абсолютных, относительных и средних величин);
- ИНДЕКСНЫЙ МЕТОД;
- ДИНАМИЧЕСКИЕ РЯДЫ;
- КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ;
- МЕТОДЫ МНОГОМЕРНОГО СТАТИСТИЧЕСКОГО АНАЛИЗА;
- МЕТОД СТАТИСТИЧЕСКИХ ГРАФИКОВ;
- БАЛАНСОВЫЙ МЕТОД.
Познавательные задачи статистики, как науки:
1)изучение уровня, структуры, динамики и взаимосвязей массовых социально-экономических явлений;
2)разработка и совершенствование системы статистических показателей, приёмов и методов сбора, обработки, анализа и хранения статистической информации.
УПРАЖНЕНИЯ
Задача 2.1. На участке месторождения 1000 скважин. Определите минимальный объем случайной бесповторной выборки, которая позволит с вероятностью 0,95 (t=1,96) оценить среднесуточный дебит с предельной ошибкой выборки 1 т/сут. Дисперсия среднесуточного дебита по данным предварительного обследования 34.
Задача 2.2. На предприятии 5000 рабочих, из них 1000 – в цехе №1, 1500 – в цехе №2, 2500 – в цехе №3. С целью определения средней выработки предполагается провести типическую выборку с пропорциональным механическим отбором рабочих внутри каждого цеха.
Какое количество рабочих следует отобрать, чтобы с вероятностью 0,997 (t=2,97) ошибка выборки не превышала 5 тыс.руб./чел.? Дисперсия выработки для типической выборки по данным предыдущих обследований 1600.
Сколько рабочих необходимо отобрать из каждого цеха?
Задача 2.3. На склад сырья и материалов предприятия поступила партия заготовок из 100 ящиков по 80 шт. в каждом. Для установления среднего веса заготовки следует провести серийную выборку методом механического отбора так, чтобы с вероятностью 0,954 (коэффициент доверия t=1,99) ошибка выборки не превысила 2 кг. На основе ранее проводимого контроля качества заготовок известно, что дисперсия серийной выборки равна 5.
Определите необходимый объем выборки (ящиков).
Задача 2.4. Для изучения уровня качества насосов проведено 10%-е выборочное обследование партии методом случайного бесповторного отбора. В результате обследования получены данные о распределении насосов по величине наработки на отказ.
| Наработка на отказ, час. | До 900 | 900 - 950 | 950 - 1000 | 1000 - 1050 | 1050 - 1100 | 1100 и более | Итого |
| Число насосов, шт. (f) | |||||||
| Центр интервала (х) | - | ||||||
| Взвешенный центр интервала (xf) | |||||||
| Квадрат центра интервала (х2) | |||||||
| Взвешенный квадрат центра интервала (х2f) |
С вероятностью 0,990 определите пределы, в которых находится среднее значение наработки на отказ во всей партии насосов. Коэффициент доверия t=2,58.
Задача 2.5. Для изучения содержания серы были взяты пробы на участке нефтяного месторождения методом 5%-ного собственно-случайного бесповторного отбора. В результате обследования проб получены следующие данные:
| Содержание серы, % | Менее 0,2 | 0,2 – 0,4 | 0,4 – 0,6 | 0,6 – 0,8 | 0,8 – 1,0 | Более 1,0 | Итого |
| Число обследованных скважин, шт. (f) | |||||||
| Центр интервала (х) | |||||||
| Взвешенный центр интервала (xf) | |||||||
| Квадрат центра интервала (х2) | |||||||
| Взвешенный квадрат центра интервала (х2f) |
С вероятностью 0,997 определите пределы, в которых находится средний уровень содержания серы по всему участку месторождения. Коэффициент доверия t=2,97.
Задача 2.6. Для планирования потребности буровой кампании в долотах проведено 10%-е выборочное обследование 100 буровых бригад методом случайного бесповторного отбора. В результате обследования получены данные о количестве израсходованных долот на одну скважину.
| Число долот, шт. | Менее 20 | 20 – 22 | 22 – 24 | 24 – 26 | 26 – 28 | 28 – 30 | 30 и более |
| Число бригад |
С вероятностью 0,954 определите пределы, в которых находится среднее число долот, израсходованных при бурении одной скважины. Коэффициент доверия t=1,99.
Задача 2.7. По действующему фонду скважин проведено 5%-ное обследование с целью измерения обводненности продукции методом случайного бесповторного отбора. В результате обследования получены следующие данные.
| Обводненность, % | До 80 | 80 – 82 | 82 – 84 | 84 – 86 | 86 – 88 | Более 88 |
| Число скважин |
С вероятностью 0,990 определите пределы, в которых находится средний уровень обводненности действующего фонда скважин. Коэффициент доверия t=2,58.
Задача 2.8. Для изучения степени износа оборудования на участке магистрального трубопровода проведено 10%-е выборочное обследование однотипных компрессоров методом случайного бесповторного отбора. В результате обследования получены данные о распределении оборудования по сроку эксплуатации.
| Срок эксплуатации, лет | Менее 5 | 5 – 8 | 8 - 11 | 11 - 14 | 14 - 17 | Более 17 |
| Число компрессоров, шт. |
С вероятностью 0,990 определите пределы, в которых находится средний срок эксплуатации компрессоров на всем участке трубопровода. Коэффициент доверия t=2,58.
Задача 2.9. Для изучения качества нефти по резервуарному парку проведен отбор проб. В результате получены данные о распределении проб по величине содержания хлористых солей.
| Содержание солей, % | Менее 0,1 | 0,1 – 0,2 | 0,2 – 0,3 | 0,3 – 0,4 | 0,4 – 0,5 | Более 0,5 | Итого |
| Число проб (f) | |||||||
| Центр интервала (х) | |||||||
| Взвешенный центр интервала (xf) | |||||||
| Квадрат центра интервала (х2) | |||||||
| Взвешенный квадрат центра интервала (х2f) |
С вероятностью 0,990 определите пределы, в которых находится средний срок эксплуатации компрессоров на всем участке трубопровода. Коэффициент доверия t=2,58.
УПРАЖНЕНИЯ
Задача 3.1. Имеются данные о пластовом давлении (в атм.) при насосном способе эксплуатации 90 скважин:
Произведите разведочный анализ выборки: 1) постройте статистический ряд распределения, определив число групп как квадратный корень из объема выборки (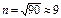 
); 2) изобразите результаты группировки в таблице, изобразите ряд распределения с помощью гистограммы, полигона и кумуляты, оцените характер распределения; 3) вычислите характеристики вариационного ряда (размах, среднее значение, моду, медиану, дисперсию, среднее квадратическое отклонение (СКО), коэффициент, вариации, структурные характеристики вариационного ряда (децили и квартили), асимметрию (скос), эксцесс), перечисленные характеристики можно вычислить с помощью встроенных статистических функций в пакете MS Excel.
Сформулируйте выводы.
Результаты построения статистического ряда распределения
| Интервалы распределения скважин по уровню пластового давления, атм. | Число скважин (частота) | Относительная частота, доли ед. | Накопленная относительная частота | Центр интервала | Взвешенный центр интервала |
| от 10 до 20 | |||||
| от 20 до 30 | |||||
| от 30 до 40 | |||||
| от 40 до 50 | |||||
| от 50 до 60 | |||||
| от 60 до 70 | |||||
| от 70 до 80 | |||||
| от 80 до 90 | |||||
| 90 и более | |||||
| Итого | - |
Результаты расчета описательных статистик распределения
| Средняя | Квартиль-1 | ||
| Мода | Квартиль-2 | ||
| Медиана | Квартиль-3 | ||
| Дисперсия | Дециль-1 | ||
| СКО (Стандартное отклонение) | Дециль-9 | ||
| Коэффициент вариации | Асимметрия | ||
| Размах | Эксцесс |
Задача 3.2. По данным о количестве израсходованных долот при механической скорости проходки 18 м/ч. на 100 скважинах
произведите разведочный анализ выборки: 1) постройте статистический ряд распределения, определив число групп как квадратный корень из объема выборки (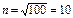 
); 2) изобразите результаты группировки в таблице, изобразите ряд распределения с помощью гистограммы, полигона и кумуляты, оцените характер распределения; 3) вычислите характеристики вариационного ряда (размах, среднее значение, моду, медиану, дисперсию, среднее квадратическое отклонение (СКО), коэффициент, вариации, структурные характеристики вариационного ряда (децили и квартили), асимметрию (скос), эксцесс), перечисленные характеристики можно вычислить с помощью встроенных статистических функций в пакете MS Excel. Сформулируйте выводы.
Результаты построения статистического ряда распределения
| Число долот, шт. | Число скважин (частота) | Относительная частота, доли ед. | Накопленная относительная частота | Центр интервала | Взвешенный центр интервала |
| от 23 до 25 | |||||
| от 25 до 27 | |||||
| от 27 до 29 | |||||
| от 29 до 31 | |||||
| от 31 до 33 | |||||
| от 33 до 35 | |||||
| от 35 до 37 | |||||
| 37 и более | |||||
| Итого | - |
Результаты расчета описательных статистик распределения
| Средняя | Квартиль-1 | ||
| Мода | Квартиль-2 | ||
| Медиана | Квартиль-3 | ||
| Дисперсия | Дециль-1 | ||
| СКО (Стандартное отклонение) | Дециль-9 | ||
| Коэффициент вариации | Асимметрия | ||
| Размах | Эксцесс |
Задача 3.3. На основе графического изображения и характеристик распределения статистического ряда проанализируйте стабильность технологического процесса первичной переработки нефти по результатам измерения температуры раздела фракции бензин-авиакеросин на установке первичной переработки нефти (в °С):
Для анализа стабильности процесса: 1) постройте статистический ряд распределения, определив число групп как квадратный корень из объема выборки (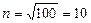 
);2) изобразите результаты группировки в таблице, изобразите ряд распределения с помощью гистограммы, полигона и кумуляты, оцените характер распределения; 3) вычислите характеристики вариационного ряда (размах, среднее значение, моду, медиану, дисперсию, среднее квадратическое отклонение (СКО), коэффициент, вариации, структурные характеристики вариационного ряда (децили и квартили), асимметрию (скос), эксцесс) и верхнюю и нижнюю границу допусков по правилу «трех сигм», перечисленные характеристики можно вычислить с помощью встроенных статистических функций в пакете MS Excel.
Сформулируйте выводы.
УПРАЖНЕНИЯ
Задача 4.1. Имеются следующие данные о добыче нефти (включая газовый конденсат) по федеральным округам России в 2010 – 2015 гг.(тыс. т).
| Российская Федерация - всего | ||||||
| Северо-Западный ФО | ||||||
| Южный ФО | ||||||
| Северо-Кавказский ФО | ||||||
| Приволжский ФО | ||||||
| Уральский ФО | ||||||
| Сибирский ФО | ||||||
| Дальневосточный ФО | ||||||
| Крымский ФО | - | - | - | - |
Вычислите абсолютные показатели добычи нефти (включая газовый конденсат) по России в целом, относительные показатели структуры и относительные показатели динамики добычи нефти (по любому из федеральных округов или России в целом) с постоянной и переменной базой сравнения. Проверьте их взаимосвязь. В качестве постоянной базы сравнения принять уровень 2010 года. При расчете показателей динамики с переменной базой сравнения каждый последующий уровень сравнивается с предыдущим смежным.
Сформулируйте выводы по результатам выполнения задания.
Результаты расчетов относительных показателей структуры (в %) представьте в следующей таблице.
| Российская Федерация - всего | ||||||
| в том числе | ||||||
| Северо-Западный ФО | ||||||
| Южный ФО | ||||||
| Северо-Кавказский ФО | ||||||
| Приволжский ФО | ||||||
| Уральский ФО | ||||||
| Сибирский ФО | ||||||
| Дальневосточный ФО | ||||||
| Крымский ФО | - | - | - | - |
Результаты расчетов относительных показателей динамики представьте в следующей таблице.
| Год | ||||||
| Добыча нефти (включая газовый конденсат), тыс. т | ||||||
| Цепной темп роста, % | - | |||||
| Цепной темп прироста, % | - | |||||
| Базисный темп роста, % | ||||||
| Базисный темп прироста, % |
Задача 4.2. По данным о добыче природного газа (в 1000 м3) на одном из предприятий рассчитайте относительные показатели. Сформулируйте выводы.
| Объем добычи газа, 1000 м3 | Относительный показатель, % | Величина | ОП – 100% | |||
| Фактически в предыдущем (базисном) году | В текущем (отчетном) году | планового задания (ОППЗ) | ||||
| по плану | фактически | выполнения плана (ОПВП) | ||||
| динамики (ОПД) |
Задача 4.3. По данным о составе фонда скважин определите относительные показатели структуры (ОПС) и координации (ОПК). Сформулируйте выводы.
| Наименование показателя | Базисный год | Отчетный | ||
| шт. | в % к итогу (ОПС) | шт. | в % к итогу (ОПС) | |
| Эксплуатационный фонд скважин - всего, | ||||
| в т.ч. | ||||
| действующие | ||||
| бездействующие | ||||
| Соотношение действующего и бездействующего фонда скважин (ОПК), раз | - | - |
Задача 4.4. По данным таблицы рассчитайте относительные показатели интенсивности (уровня развития), используя следующие данные по РФ за 2015 г. Сформулируйте выводы.
| Наименование показателя | Величина | |
| Абсолютные показатели: | ||
| Среднегодовая численность населения, тыс. чел. | 146406,0 | |
| Среднегодовая численность занятых в экономике, тыс. чел. | 68389,1 | |
| Валовой региональный продукт, млрд. р. | 58900,7 | |
| Основные фонды в экономике, млрд. р. | ||
| Объем отгруженных товаров собственного производства по видам экономической деятельности, млрд. руб.: | ||
| добыча полезных ископаемых | 11170,6 | |
| обрабатывающие производства | 33087,2 | |
| производство и распределение электроэнергии, газа и воды | 4833,4 | |
| Относительные показатели интенсивности (уровня развития): | ||
| Уровень занятости в % к численности населения | ||
| Объем отгруженных товаров собственного производства на душу населения по видам экономической деятельности (указать единицы измерения самостоятельно): | ||
| добыча полезных ископаемых, | ||
| обрабатывающие производства, | ||
| производство и распределение электроэнергии, газа и воды, | ||
| Валовой региональный продукт на душу населения, (указать единицы измерения самостоятельно) | ||
| Фондовооруженность занятых в экономике, (указать единицы измерения самостоятельно) |
Задача 4.5. Используя значения признаков по участкам месторождений, определите средние показатели по месторождению в целом. Формулы запишите, используя буквенные обозначения признаков. Укажите виды использованных средних величин.
| Участок | Действующий среднегодовой фонд скважин, шт. | Коэффициент эксплуатации скважин, д. ед. | Средний дебит одной скважины, т/сут. | Среднее время работы одной скважины за год, сут. | Среднегодовая выработка одного работника, т/чел. |
| n | k | q | t | w | |
| 0,783 | |||||
| 0,856 | |||||
| 0,987 | |||||
| 0,965 | |||||
| Средняя |
Тема 5. ПОКАЗАТЕЛИ ВАРИАЦИИ
ВАРИАЦИЯ – (в переводе с лат. – изменение, колеблемость, различие) это различие значений какого-либо признака у разных единиц совокупности в один и тот же период или момент времени.
Вариация порождается комплексом условий, действующих на совокупность и её единицы, и присуща всем без исключения явлениям природы и общества (за исключением законодательно закреплённых нормативных значений отдельных социальных признаков).
Измерение вариации даёт возможность оценить степень влияния на изучаемый признак других варьирующих признаков. Например, установить, какие факторы и в какой степени влияют на смертность населения, финансовое положение предприятий, урожайность пшеницы и т. п.
Для измерения вариации признака применяются различные обобщающие показатели.
1. Размах колебаний (вариации) (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности: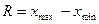 
.
2. Формулы для расчёта среднего линейного отклонения, дисперсии, среднего квадратического отклонения зависят от того, в каком виде представлены данные (сгруппированы они или нет) (таблица 6).
Таблица 6 – Показатели вариации
| Показатель | Для первичного ряда (по несгруппированным данным) | Для вариационного ряда (по сгруппированным данным) |
| Среднее линейное отклонение |  |  |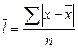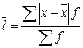
| Дисперсия |  |  |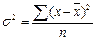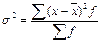
| Среднее квадратическое отклонение |  |  |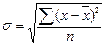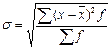
Качественные (альтернативные) признаки, так же как и количественные варьируют (изменяются). Вариация альтернативного признака оценивается с помощью показателя дисперсии, определяемого по формуле: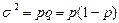 
, где p – доля единиц, обладающих данным признаком; q – доля единиц, не обладающих данным признаком.
При сравнении колеблемости различных признаков в одной и той же совокупности или при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной средней арифметической используются относительные показатели рассеивания (вариации). К относительным показателям вариации относятся:
1) коэффициент осцилляции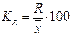 
;
2) относительное линейное отклонение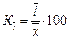 
;
3) коэффициент вариации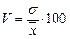 
, используется для оценки типичности средней величины признака. Совокупность считается однородной, а средняя типичной для данной совокупности, если коэффициент вариации не больше 33 %.
Для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений признака, используется разложение общей дисперсии на составляющие: межгрупповую дисперсию и среднюю дисперсию из внутригрупповых.
Общая дисперсия рассчитывается по всей совокупности и характеризует вариацию признака, обусловленную влиянием всех факторов, действующих в совокупности:
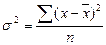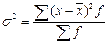 - простая дисперсия; |  - взвешенная дисперсия |
Межгрупповая дисперсия (является мерой колеблемости частных или групповых средних вокруг общей средней) характеризует вариацию признака, обусловленную влиянием фактора, положенного в основу группировки: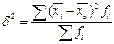 
.
Вариацию признака под влиянием прочих факторов (помимо признака-фактора, положенного в основу группировки), действующих в совокупности, характеризует средняя дисперсия из внутригрупповых (частных) дисперсий: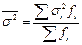 
.
Внутригрупповая (частная) дисперсия: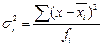 
, отражает вариацию признака только за счёт условий и причин, действующих внутри группы.
Между названными видами дисперсий существует определённое соотношение, которое называют ЗАКОНОМ (правилом) сложения дисперсий: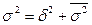 
.
Отношение межгрупповой дисперсии к общей даст коэффициент детерминации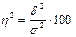 
, который характеризует долю вариации результати<