Случайные события и величины, их основные характеристики

Основные понятия математической статистики

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

Часть 2

Распределение Пуассона

Распределение Пуассона относится к тем случаям, когда число случайных событий происходит на определенной длине площади, объеме или времени. Здесь основным определяющим параметром распределения является среднее число событий т. Распределение вероятности для х имеет следующий вид:

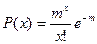, где m=np.

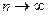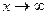Распределение Пуассона аппроксимирует биномиальные распределения в пределе, когда , а так, что среднее пр = т - const.

Таким образом, распределение Пуассона является предельным для биномиального распределения, когда вероятность ( 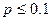) мала, число событий велико, а математическое ожидание появления дефектных изделий является ограниченным числом.

Это распределение иногда называют законом распределения редких событий.

Контрольное задание № 2

По данным таблицы 3.1 оценить вероятность появления бракованных изделий и кумулятивную вероятность для данной выборки. Результаты расчетов занести в таблицу 2.2. Построить графики плотности вероятности и кумулятивной вероятности. Сделать выводы.

Таблица 3.1

№ варианта	Число дефектных изделий х, шт	Вероятность получения дефектных изделий p	Вероятность получения годных изделий q	Объем выборки п
1		3	4	5
	0-10	0,005	0,995
	0-9	0,004	0,996
	0-8	0,003	0,997
	0-7	0,002	0,998
	0-6	0,02	0,'98
	0-5	0,007	0,993
	0-11	0,01	0,99
	0-12	0,02	0,98
	0-13	0,03 | 0,97	0,97
	0-14	0,015 1 0,985	0,985

Нормальный закон распределения

ЛИТЕРАТУРА

1.Управление качеством: Том 1 и 2. Принципы и методы всеобщего руководства качеством / Под общ.ред. Азарова В.Н., М.: МГИЭМ, 2000.

2. Огвоздин В.Ю. Управление качеством. Основы теории и практики: Учебное пособие. - М.: Изд-во «Дело и сервис», 1999. - 160 с.

3. Басовский Л.Е., Протасьев В.Б. Управление качеством: Учебник. - М.: ИНФРА-М. 2000.-212с.

4. Фомин В.Н. Квалиметрия. Управление качеством. Сертификация. Курс лекций. - М.: Ассоциация авторов и издателей «ТАНДЕМ». Издательство «ЭКМОС», 2000. - 320 с.

5. Басовский Л.Е. Теория экономического анализа: Учебное пособие. - М.: ИНФРА-М. 2001.-222 с.

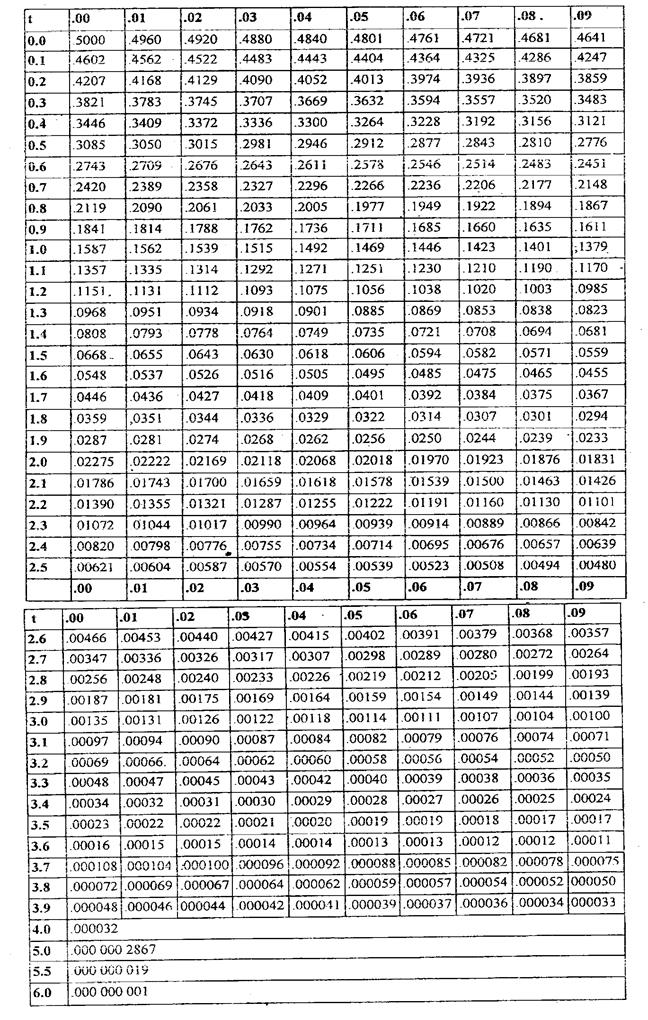
Приложение 1 Таблица 1

Значения функции

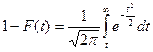
определяют долю площади под кривой распределения, ограниченной пределами от 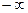до t, где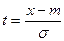

Основные понятия математической статистики

Случайные события и величины, их основные характеристики

Как уже говорилось, при анализе больших систем наполнителем каналов связи между элементами, подсистемами и системы в целом могут быть:

· продукция, т. е. реальные, физически ощутимые предметы с заранее заданным способом их количественного и качественного описания;

· деньги, с единственным способом описания — суммой;

· информация, в виде сообщений о событиях в системе и значениях описывающих ее поведение величин.

Начнем с того, что обратим внимание на тесную (системную!) связь показателей продукции и денег с информацией об этих показателях. Если рассматривать некоторую физическую величину, скажем — количество проданных за день образ­цов продукции, то сведения об этой величине после продажи могут быть получены без проблем и достаточно точно или достоверно. Но, уже должно быть ясно, что при системном анализе нас куда больше интересует будущее — а сколько этой продукции будет продано за день? Этот вопрос совсем не праздный — наша цель управлять, а по об­разному выражению “управлять — значит предвидеть”.

Итак, без предварительной информации, знаний о количественных показателях в системе нам не обой­тись. Величины, которые могут принимать различные значения в зависимости от внешних по отношению к ним условий, принято называть случайными (стохастичными по природе). Так, например: пол встреченного нами человека может быть женским или мужским (дискретная случайная величина); его рост также может быть различным, но это уже непрерывная случайная величина — с тем или иным количеством возможных значений (в зависимости от единицы измерения).

Для случайных величин (далее — СВ) приходится использовать особые, статистические методы их описания. В зависимости от типа самой СВ — дискретная или непрерывная это делается по разному.

Дискретное описание заключается в том, что указываются все возможные значения данной величины (например - 7 цветов обычного спектра) и для каждой из них указывается вероятность или частота наблюдений именного этого значения при бесконечно большом числе всех наблюдений.

Можно доказать (и это давно сделано), что при увеличении числа наблюдений в определенных усло­виях за значениями некоторой дискретной величины частота повторений данного значения будет все больше приближаться к некоторому фиксированному значению — которое и есть вероятность этого значения.

К понятию вероятности значения дискретной СВ можно подойти и иным путем — через случайные собы­тия. Это наиболее простое понятие в теории вероятностей и математической статистике — событие с вероятностью 0.5 или 50% в 50 случаях из 100 может произойти или не произойти, если же его вероятность более 0.5 - оно чаще происходит, чем не происходит. События с вероятностью 1 называют достоверными, а с вероятностью 0 — невозможными.

Отсюда про­стое правило: для случайного события X вероятности P(X) (событие происходит) и P(X) (событие не происходит), в сумме для простого события дают 1.

Если мы наблюдаем за сложным событием — например, выпадением чисел 1..6 на верхней грани игральной кости, то можно считать, что такое событие имеет множество исходов и для каждого из них вероятность составляет 1/6 при симметрии кости.

Если же кость несимметрична, то вероятности отдельных чисел будут разными, но сумма их равна 1.

Стоит только рассматривать итог бросания кости как дискретную случайную величину и мы придем к понятию распределения вероятностей такой величины.

Пусть в результате достаточно большого числа наблюдений за игрой с помощью одной и той же кости мы получили следующие данные:

Таблица 2.1

Грани							Итого
Наблюдения

Подобную таблицу наблюдений за СВ часто называют выборочным распределением, а соответствующую ей картинку (диаграмму) — гистограммой.

Рис. 2.1

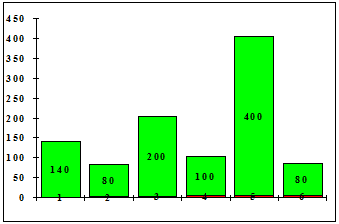
Какую же информацию несет такая табличка или соответствующая ей гистограмма?

Прежде всего, всю — так как иногда и таких данных о значениях случайной величины нет и их приходится либо добывать (эксперимент, моделирование), либо считать исходы такого сложного события равновероятными — по 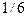на любой из исходов.

С другой стороны — очень мало, особенно в цифровом, численном описании СВ. Как, например, ответить на вопрос: — а сколько в среднеммы выигрываем за одно бросание кости, если выигрыш соответствует выпавшему числу на грани?

Нетрудно сосчитать:

1•0.140+2•0.080+3•0.200+4•0.400+5•0.100+6•0.080= 3.48

То, что мы вычислили, называется средним значением случайной величины, если нас интересует прошлое.

Если же мы поставим вопрос иначе — оценить по этим данным наш будущий выигрыш, то ответ 3.48 принято называть математическим ожиданиемслучайной величины, которое в общем случае определяется как

Mx = å X_i·P(X_i); {2 - 1}

где P(X_i) — вероятность того, что X примет свое i-е очередное значение.

Таким образом, математическое ожидание случайной величины (как дискретной, так и непрерывной)— это то, к чему стремится ее среднее значение при достаточно большом числе наблюдений.

Обращаясь к нашему примеру, можно заметить, что кость несимметрична, в противном случае вероятности составляли бы по 1/6 каждая, а среднее и математическое ожидание составило бы 3.5.

Поэтому уместен следующий вопрос - а какова степень асимметрии кости - как ее оценить по итогам наблюдений?

Для этой цели используется специальная величина — мера рассеяния — так же как мы "усредняли" допустимые значения СВ, можно усреднить ее отклонения от среднего. Но так как разности (X_i - Mx)всегда будут компенсировать друг друга, то приходится усреднять не отклонения от среднего, а квадраты этих отклонений. Величину

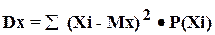{2 - 2}

принято называть дисперсией случайной величины X.

Вычисление дисперсии намного упрощается, если воспользоваться выражением

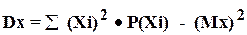{2 - 3}

т. е. вычислять дисперсию случайной величины через усредненную разность квадратов ее значений и квадрат ее среднего значения.

Выполним такое вычисление для случайной величины с распределением рис. 1.

Таблица 2.2

Грани(X)							Итого
X2
Pi	0.140	0.080	0.200	0.400	0.100	0.080	1.00
Pi•X2•1000

Таким образом, дисперсия составит 14.04 - (3.48)² = 1.930.

Заметим, что размерность дисперсии не совпадает с размерностью самой СВ и это не позволяет оценить величину разброса. Поэтому чаще всего вместо дисперсии используется квадратный корень из ее значения — т. н. среднеквадратичное отклонение или отклонение от среднего значения:

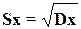{2 - 4}

составляющее в нашем случае 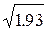= 1.389. Много это или мало?

Сообразим, что в случае наблюдения только одного из возможных значений (разброса нет) среднее было бы равно именно этому значению, а дисперсия составила бы 0. И наоборот - если бы все значения наблюдались одинаково часто (были бы равновероятными), то среднее значение составило бы (1+2+3+4+5+6) / 6 = 3.500; усредненный квадрат отклонения — (1 + 4 + 9 + 16 + 25 + 36) / 6 =15.167; а дисперсия 15.167-12.25 = 2.917.

Таким образом, наибольшеерассеяние значений СВ имеет место при ее равновероятном или равномерном распределении.

Отметим, что значения Mxи S_X являются размерными и их абсолютные значения мало что говорят. Поэтому часто для грубой оценки "случайности" данной СВ используют т. н. коэффициент вариации или отношение корня квадратного из дисперсии к величине математического ожидания:

V_x = S_X/M_X . {2 - 5}

В нашем примере эта величина составит 1.389/3.48=0.399.

Итак, запомним, что неслучайная, детерминированная величина имеет математическое ожидание равное ей самой, нулевую дисперсиюи нулевой коэффициент вариации, в то время как равномерно распределенная СВ имеет максимальную дисперсию и максимальный коэффициент вариации. Коэффициент вариации используют для сравнения рассеивания двух и более признаков, имеющих различные единицы измерения. Коэффициент вариации представляет собой относительную меру рассеивания, выраженную в процентах

В ряде ситуаций приходится иметь дело с непрерывно распределенными СВ - весами, расстояниями и т. п. Для них идея оценки среднего значения (математического ожидания) и меры рассеяния (дисперсии) остается той же, что и для дискретных СВ. Приходится только вместо соответствующих сумм вычислять интегралы. Второе отличие — для непрерывной СВ вопрос о том какова вероятность принятия нею конкретного значения обычно не имеет смысла — как проверить, что вес товара составляет точно 242 кг - не больше и не меньше?

Для всех СВ — дискретных и непрерывно распределенных, имеет очень большой смысл вопрос о диапазоне значений. В самом деле, иногда знание вероятности того события, что случайная величина не превзойдет заданный рубеж, является единственным способом использовать имеющуюся информацию для системного анализа и системного подхода к управлению. Правило определения вероятности попадания в диапазон очень просто — надо просуммировать вероятности отдельных дискретных значений диапазона или проинтегрировать кривую распределения на этом диапазоне.