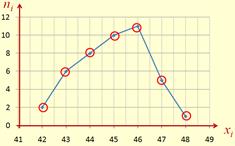
Cоставим дискретный вариационный ряд.

Все варианты расположим в порядке возрастания в первой строке таблицы, а частоту, с которой они встречаются в данной выборке во второй строке.

xi
ni

Объем выборки n=43.

Построим полигон.

Для построения полигона на оси OX отложим значения вариант x_i, а на оси OY – значения частот n_i.

Вычислим средние характеристики.

а) Определим среднее выборочное :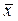

,

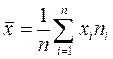Вычисления оформим в виде таблицы:

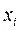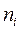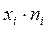		å=1933

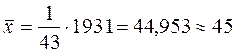
б) Определим моду :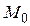

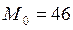
в) Определить медиану :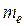

Выборку сначала необходимо проранжировать:

42 42 43 43 43 43 43 43 44 44

44 44 44 44 44 44 45 45 45 45

45 45 45 45 45 45 46 46 46 46

46 46 46 46 46 46 46 47 47 47

47 47 48

Объем выборки n=43 является нечетным числом, следовательно 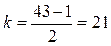, значит, 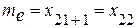, то есть 22-ой по счету вариант в ранжированном ряду и будет медианой: .

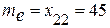Вычислим характеристики вариации.

а) Определим размах вариации :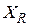

,

.

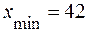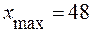
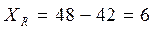б) Определим дисперсию D:

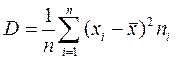, где

Вычисления оформим в виде таблицы:

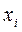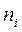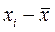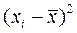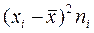		-3
		-2
		-1
				å=90

.

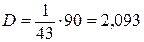в) Определим среднее квадратическое отклонение s:

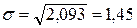(≈1).

г) Определим коэффициент вариации V:

.

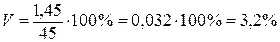д) Определим ошибку выборочного среднего :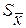

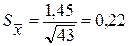(≈0).

5. Вывод. По данным числа отжиманий в упоре лежа 43 испытуемых средний результат составил 45 раз ± 0 раз. Степень рассеяния данных выборки от среднего результата составляет 1 отжимание. Чаще всего встречаемый результат в группе – 46 отжиманий. Одна половина спортсменов показала результаты лучше 45 отжиманий, а другая половина хуже. Отклонение результатов числа отжиманий в упоре лежа внутри группы равно 6 отжиманиям. Результаты исследования имеют малую варьируемость, что говорит об однородности выборки, то есть средний результат типичен для изучаемого признака.

Пример 2

Задание: По данным выборки:

1. Составить интервальный вариационный ряд.

2. Начертить гистограмму.

3. Найти средние характеристики:

а) среднюю выборочную ;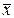

б) моду ;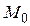

в) медиану .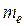

4. Найти характеристики вариации:

а) размах вариации ;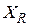

б) дисперсию D;

в) среднее квадратическое отклонение s;

г) коэффициент вариации V;

д) ошибку выборочного среднего .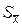

Исходные данные: Бег на 100 м (юноши 9 классов).

16,2 15,5 14,3 16,6 15,8 15,4 14,5 14,8 16,1 15,8

15,3 16,0 13,7 16,1 16,2 15,3 15,5 14,8 14,3 16,2

15,3 15,8 14,2 15,8 14,2 15,4 14,7 12,8 16,9 15,0

16,8 16,0 14,6 15,6 16,1 17,8 15,6 15,0 15,6 15,0

16,2 15,5 13,6 16,4 15,2 15,9 15,0 14,2 16,4 14,2

Этапы выполнения:

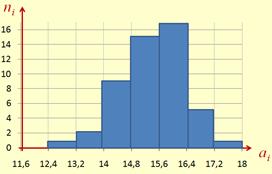
Cоставим интервальный вариационный ряд.

n=50, по приложению 1 найдем значение lg50=1,6990.

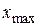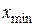=17,8 =12,8

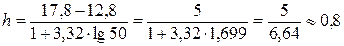(значение величины интервала округляем с точностью до десятых, так как исходные данные имеют точность до десятых долей).

Найдем границы интервалов. Левой границей первого интервала будет число 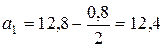. Вычисляем далее

,

,

,

,

,

,

.

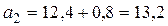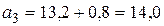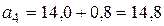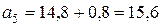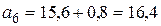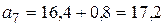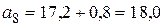Значение границы 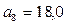больше максимального значения выборки

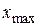=17,8, поэтому останавливаемся вычислять границы интервалов.

Результаты оформляем в таблицу:

Интервалы	12,4-13,2	13,2-14,0	14,0-14,8	14,8-15,6	15,6-16,4	16,4-17,2	17,2-18,0
Частоты

Получили интервальный вариационный ряд.

Построим гистограмму.