II Образец выполнения заданий расчетно-графической работы

Задача 1. Математико-статистическая модель лесной экосистемы

Цель работы:получить представление о способах построения математико-статистических моделей, о методах обработки собственно-случайной выборки, познакомиться с основными статистическими показателями и уяснить их практический смысл. Научиться вычислять статистические показатели с помощью ППП Mathcad.

Порядок выполнения задачи:

1.Записать данные наблюдения согласно полученному заданию.

2.Провести первичную обработку данных наблюдения и построить статистическое распределение выборки с помощью встроенных функций ППП Mathcad.

3.Построить полигон и гистограмму. По виду гистограммы (или полигона) выдвинуть гипотезу о законе распределения исследуе­мой случайной величины.

4.Вычислить основные статистические показатели: выборочную среднюю, выборочную дисперсию, среднее квадратическое отклонение, коэффициент вариации, асимметрию и эксцесс с помощью ППП Mathcad.

5.Найти ошибки полученных показателей и относительную ошиб­ку выборочной средней. Определить достоверность статистических показателей для 5% - ного уровня значимости, пользуясь критерием Стьюдента.

6.Проверить по критерию Пирсона гипотезу о нормальном распределении генеральной совокупности при уровне значимости α = 0,05.

7.Вычислить доверительные интервалы для генерального среднего, для коэффициента вариации и среднего квадратического отклонения в генераль­ной совокупности.

8.Провести анализ результатов полученной математико-статистической модели и сделать выводы.

Задача 1.

1. Данные наблюдения: масса одной луковицы тюльпана сорта «Патриот» в граммах при среднем числе растений 30 шт/м²

Выборочная совокупность содержит результаты 50 наблюдений и поэтому она является большой выборкой. Для выполнения сводки данных наблюдения необходимо все данные разбить на k интервалов одинаковой длины. Число интервалов определяют по приближенной формуле Стерджесса:

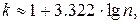
где 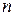- объем выборки. Число интервалов округляем до целого числа. В нашем случае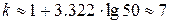

Длину интервала определяем так: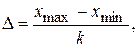

где 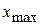- наибольший элемент выборки; 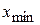- наименьший элемент выборки.

Длину интервала вычисляют с точностью выборки. В нашем примере:

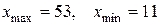. Тогда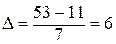

Границы интервалов вычисляем по формуле:

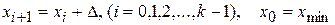
Все эти операции выполняются в среде Mathcad (Рисунок 6).

После определения границ интервалов производим сводку данных наблюдений с помощью ППП Mathcad. Далее приведен фрагмент рабочего документа Mathcad, выполняющий эти функции (Рисунок 7).

2. Интервальный ряд распределения, полученный по сводке данных наблюдения, запишем в виде таблицы 3.

Таблица 3 – Интервальный ряд распределения частот

Интервалы	11 - 17	17 - 23	23 - 29	29 - 35	35 - 41	41 - 47	47 - 53
Частота

Ряд распределения (статистический ряд) характеризуется значением вариант, представляющих собой величины середин каждого интервала и соответствующих им частот. Тогда ряд распределения можно записать в виде таблицы 4 и таблицы 5.

Рисунок 6 – Первичная обработка результатов измерений в среде Mathcad.

Таблица 4 – Статистический ряд распределения частот

Значение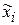
Частота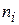

Таблица 5 – Ряд распределения относительных частот

Значение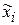
Относительная частота	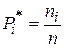0.04	0.1	0.2	0.34	0.14	0.1	0.08

Результат обработки выборочной совокупности, представленный таблицей 4, называется статистическим рядом распределения частот признака 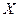, а в виде таблицы 5 – рядом распределения относительных частот этого же признака.

Рисунок 7 – Выполнение сводки данных наблюдения.

3. Для построения гистограммы относительных частот необходимо знать длины интервалов 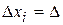(основания прямоугольников) и высоты 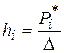(плотность относительной частоты). Все необходимые данные вычислим в Mathcad и занесем в таблицу 6.

Таблица 6– Ряд распределения плотности относительной частоты

Значение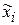
Плотность	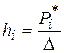0.007	0.017	0.033	0.057	0.023	0.017	0.013

Строим гистограмму относительных частот (рисунок 8). Соединяя середины верхних сторон прямоугольников отрезками прямых линий, получаем полигон относительных частот (ломаная линия).

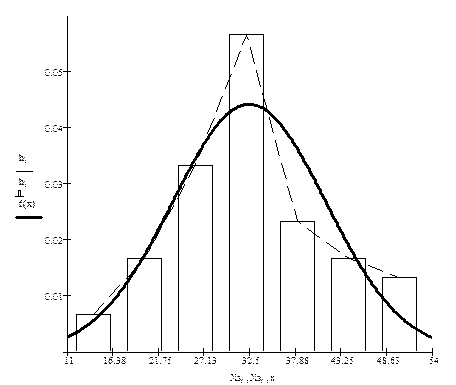
Рисунок 8 – Полигон и гистограмма относительных частот. Теоретическая кривая нормального распределения.

По виду гистограммы (полигона) выдвигаем гипотезу о нормальном распределении данного признака Х – массы одной луковицы тюльпана.

4. Вычислим основные статистические показатели с помощью ППП Mathcad (Рисунок 9).

Так как 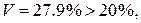следовательно, изменчивость данного признака является значительной.

Так как А>0, то асимметрия – левосторонняя. Эксцесс Е<0, следовательно, линия распределения вариант данного ряда проходит ниже кривой нормального распределения.

5. Вычисление ошибок среднего выборочного значения, среднего квадратичного отклонения, коэффициентов вариации, асимметрии и эксцесса производится с использованием программы Mathcad (Рисунок 10).

Кроме абсолютной ошибки выборочной средней определим и ее относительную ошибку:

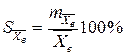
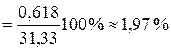
Следовательно, если утверждать, что генеральная средняя равна полученной выборочной средней, то ошибка при этом составит примерно 1,97%.

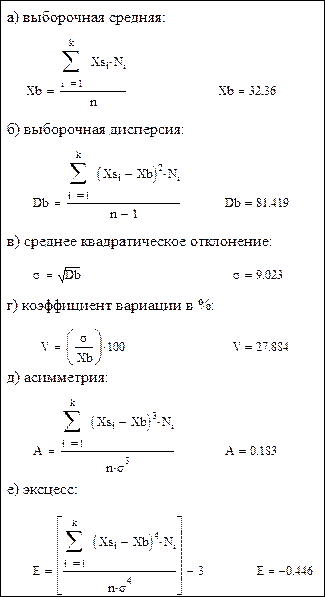
Рисунок 9 – Расчет основных статистических показателей.

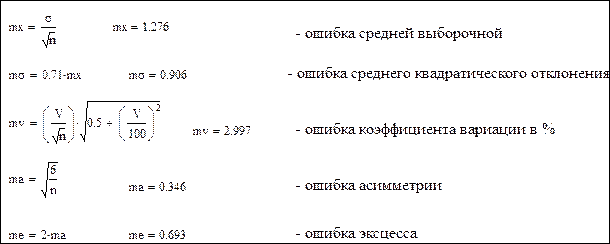
Рисунок 10 – Определение ошибок основных статистических показателей.

Оценка достоверности показателей производится путем вычисления отношения величины рассматриваемого показателя к его ошибке:

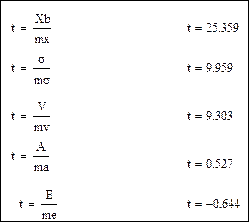
Сравниваем полученные показатели достоверности со стандартной величиной t(k, 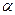), при числе степеней свободы k=n–1=200–1=199 и уровне значимости 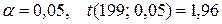(Приложение 1). Так как значения показателей достоверности для выборочной средней, среднего квадратичного отклонения и коэффициента вариации больше, чем 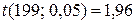, то перечисленные статистические показатели достоверны на 5%-ном уровне значимости. Значения показателей достоверности для асимметрии и эксцесса оказываются меньше, чем 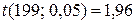, следовательно, асимметрия и эксцесс недостоверны на 5%-ном уровне значимости, и можно считать, что косость и крутость у эмпирической кривой распределения практически отсутствуют, то есть 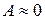и .

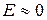6. При заданном уровне значимости 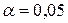проверим по критерию Пирсона гипотезу о нормальном распределении генеральной совокупности. Для этого необходимо найти теоретические частоты :

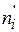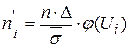
где n - объем выборки; 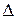- длина интервала; - выборочное среднее квадратическое отклонение;

,

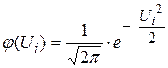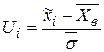
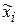- середины интервалов (i=1,2, … 7); 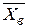- выборочное среднее. Значения функции 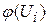можно найти по таблице приложения 3.

В данной задаче n=50, 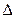= 6, = 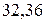, = 9,02. Тогда имеем:

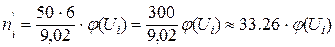
Определим 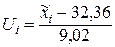, а по таблице приложения 3 соответствующее значение 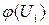. Все необходимые вычисления выполним в Mathcad и сведем в таблицу 7.

Таблица 7 – Расчет теоретических частот

i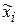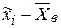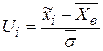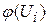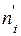
		-18.36	-2.035	0.0498	1.674
		-12.36	-1.370	0.1561	5.191
		-6.36	-0.705	0.3101	10.346
		-0.36	-0.040	0.3986	13.253
		5.64	0.625	0.3271	10.910
		11.64	1.290	0.1736	5.772
		17.64	1.955	0.0584	1.962

Сравним эмпирические ( 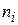) и теоретические ( 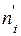) частоты с помощью критерия Пирсона:

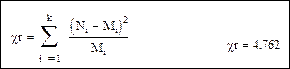
По таблице критических точек распределения 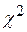(Приложение 4) с заданным уровнем значимости 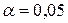и числу степеней свободы 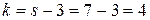находим критическую точку правосторонней критической области 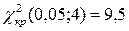. Так как 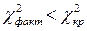, то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Таким образом, масса луковиц распределена по нормальному закону, и мы можем построить теоретическую кривую распределения с плотностью распределения

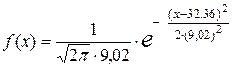
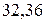= , = 9,02

Вычисление значений 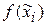можно провести с помощью встроенной функции Mathcad 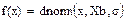. Строим теоретическую кривую распределения на рисунке 8 (сплошная жирная линия).

7. Вычислим доверительный интервал для средней в генеральной совокупности по формуле

,

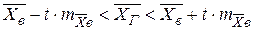причем = 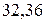, 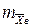= 1,276,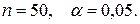

По таблице приложения 3 находим 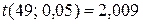, тогда получаем:

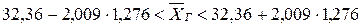
или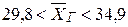

Аналогично определим доверительный интервал для среднего квадратического отклонения в генеральной совокупности по формуле:

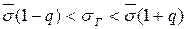
По таблице приложения 4 находим значение 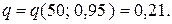Тогда имеем:

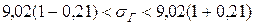
или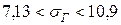

8. Для проведения анализа запишем кратко полученные результаты в следующей последовательности:

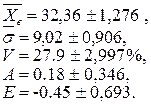
На основании этих результатов можно сделать следующие выводы:

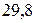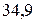– выборочная средняя массы одной луковицы тюльпана сорта «Патриот» в граммах при среднем числе растений 30 шт/м² составляет 32,36 г, а генеральная средняя изучаемого признака Х находится в интервале от до г.

– изменчивость массы луковиц характеризуется средним квадратическим отклонением, которое для выборочной совокупности составляет 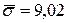г, коэффициент вариации равен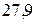 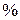, что говорит о значительной изменчивости Х. В генеральной совокупности среднее квадратическое отклонение находится в интервале от 7,13 г до 10,9 г.

– оценка достоверности основных статистических показателей приводит к выводу о надежности выборочной средней, среднего квадратического отклонения и коэффициента вариации на 5%-ном уровне значимости. В то же время такие показатели, как асимметрия и эксцесс, характеризующие косость и крутость эмпирической кривой, недостоверны, что позволяет считать их практически отсутствующими.

– на основании проверки критерия согласия Пирсона мы приходим к выводу о том, что изучаемый признак Х – масса одной луковицы в граммах при среднем числе растений 30 шт/м² можно считать распределенным по нормальному закону с плотностью распределения

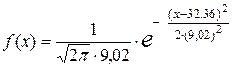
Полный текст программы, с помощью которой проводились все вычисления в среде Mathсad смотри в приложении 6.