Системы уравнений и неравенств
Системы уравнений
В школьной программе изучают системы двух уравнений с двумя неизвестными. Различают аналитические способы (способ подстановки и способ сложения или способ уравнивания коэффициентов) и графический способ.
Способ подстановки:
1. Одну из переменных выразить через другую (какую и из какого уравнения – выберите наиболее простой вариант).
2. Подставить это выражение в другое уравнение.
3. Решить это уравнение, найти переменную.
4. Вычислить другую переменную.
5. Записать ответ.
Пример:
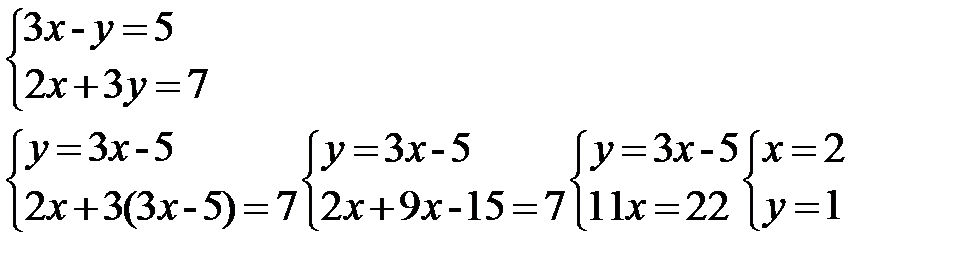
Ответ: (2;1)
Способ сложения - основан на свойстве систем, по которому уравнения системы можно умножать , делить на число, не равное 0, и складывать друг с другом или вычитать.
Пример:
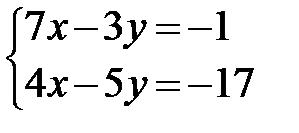
Первое уравнение умножаю на 5, второе –на (-3), уравнивая коэффициенты при х: 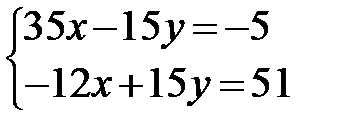 . Складываю уравнения системы: 23х=46, х=2. Из первого уравнения: 7*2-3у=-1, -3у=-15, у=5.
. Складываю уравнения системы: 23х=46, х=2. Из первого уравнения: 7*2-3у=-1, -3у=-15, у=5.
Ответ: (2;5)
Решите системы:
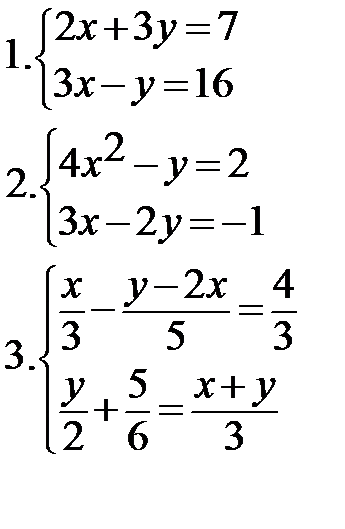 | 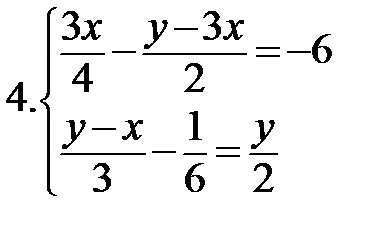 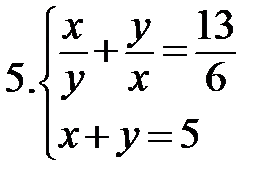 * * | 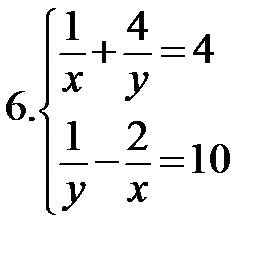 * * 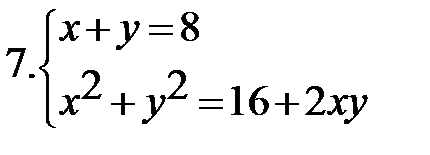 ** ** |
* - введите новую переменную
** - используйте формулу сокращенного умножения.
Системы неравенств
Если вы успешно решаете неравенства, то также успешно сможете решать системы неравенств, т.к. для того, чтобы решить систему неравенств, достаточно решить каждое неравенство в отдельности и найти общее решение.
Примеры:
1.Решите систему неравенств
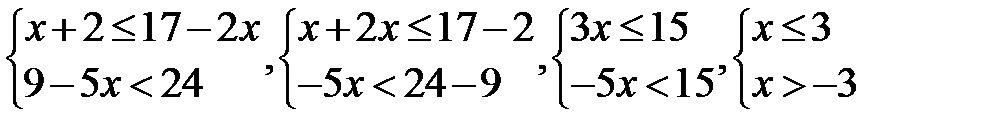
Решение системы неравенств:
-3 3 х
Ответ: -3< x≤3
Самостоятельно:
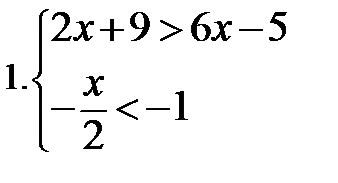 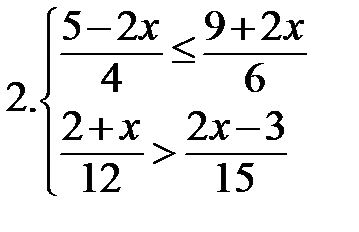 | 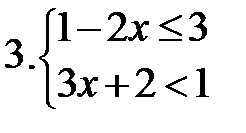 Сколько целых решений имеет система? Сколько целых решений имеет система? 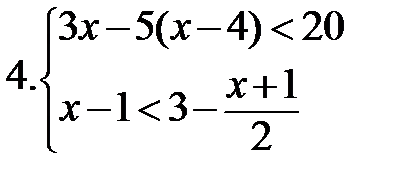 |
1.7.3.Индивидуальные задания
ИЗ-7: Решение систем уравнений и неравенств 1 вариант 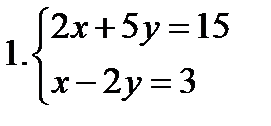 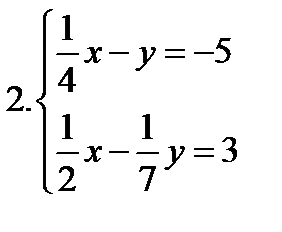 3. 3. 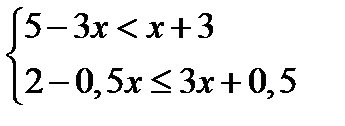 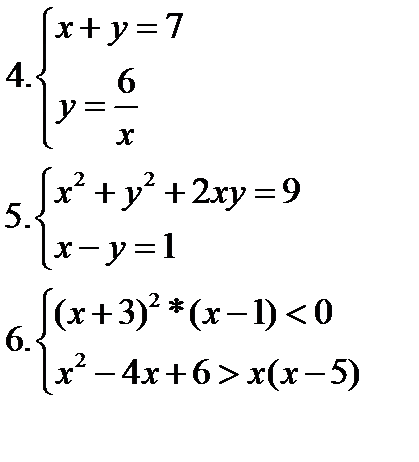 | Критерии оценки: Цена каждого задания-3 балла. «3»-9 баллов, «4» -12-15 баллов, «5» -16-18. | ИЗ-7: Решение систем уравнений и неравенств 3вариант 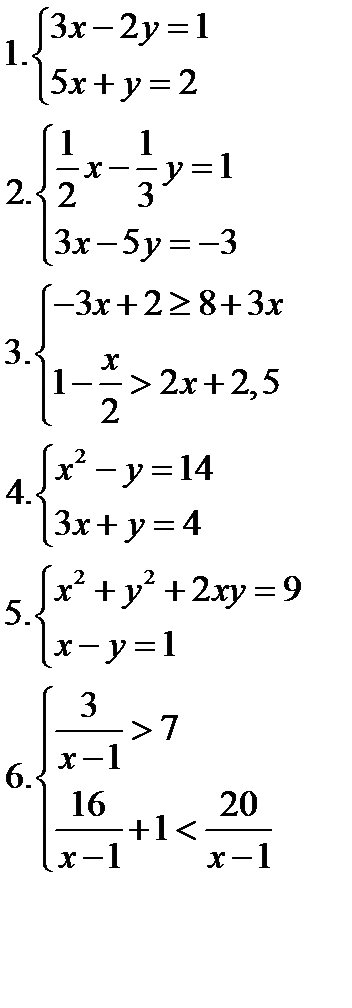  |
ИЗ-7: Решение систем уравнений и неравенств 4вариант 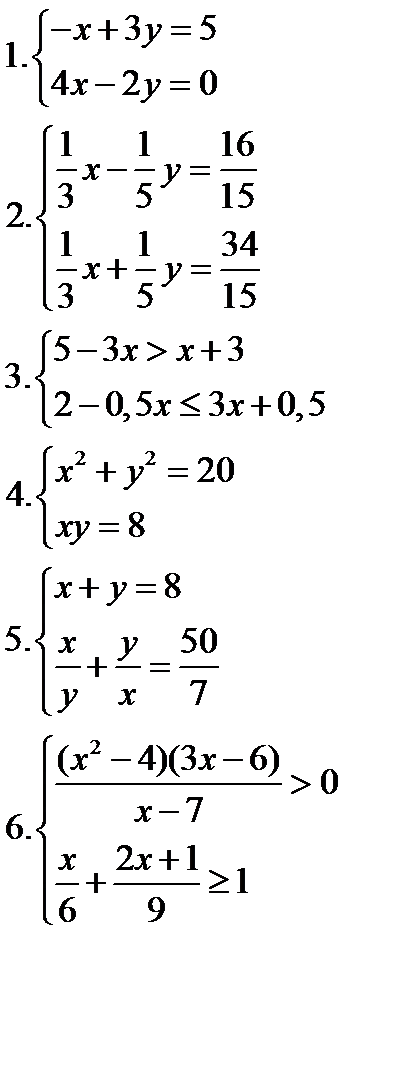 | Критерии оценки: Цена каждого задания-3 балла. «3»-9 баллов, «4» -12-15 баллов, «5» -16-18. | ИЗ-7: Решение систем уравнений и неравенств 2 вариант 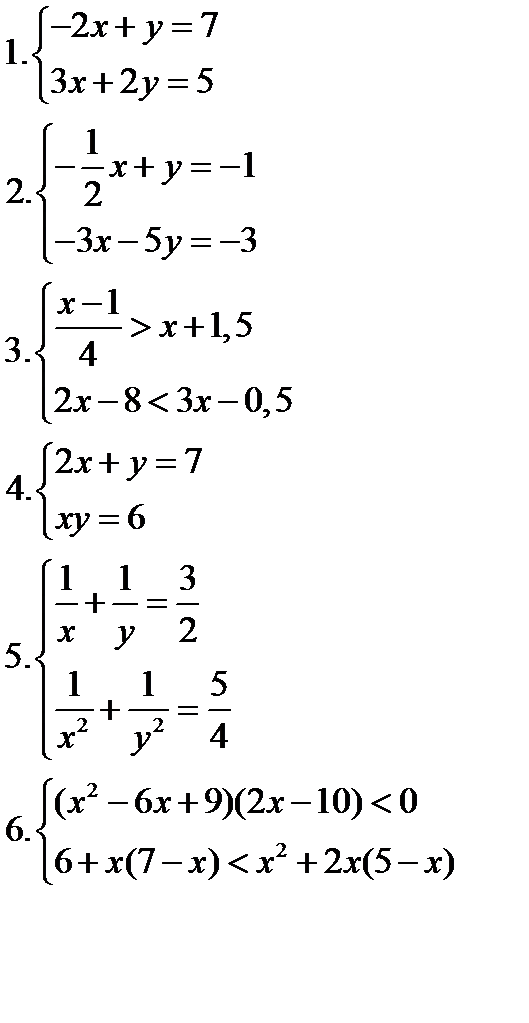 |
Функции: свойства, графики
Класс функций, которые изучаются в школьной программе, называют классом элементарных функций. К ним относят:
· Линейную функцию
· Квадратичную
· Кубическую
· Обратную пропорциональную и некоторые другие.
Рассмотрим некоторые из них подробно, другие обзорно.
Линейная функция
Определение:
Линейной функцией называется функция, имеющая вид:
у = ах+в,
где а, в – любые действительные числа, х – независимая переменная.
Графиком линейной функции является прямая линия:
У у=ах+в
| в |
α
X
Смысл коэффициентов а и в:
в - показывает точку пересечения с осью ординат (у),
а – угловой коэффициент, численно равен тангенсу угла наклона прямой к положительному направлению оси абсцисс (х), а = tgα.
Прямая строится «по точкам». Для этого составляется таблица:
| х | ах+в=0, х=… | |
| у | в |
Попробуем изучить свойства функции экспериментально:
Разобьемся на 4 группы, выполним следующие задания:
1. Постройте графики функций:
1 группа 2 группа 3 группа 4 группа
| 1.у1 = 2х - 3 2.у2 = 5х + 10 3. у3 = 1/2х-4 4.у4 = 4х 5. у5 = х | 1.у1 = - 2х + 3 2.у2 = -4х + 1 3. у3 = - х/3 +2 4.у4 = - 2х 5. у5 = - х | 1.у1 = 2 2.у2 = 0 3. у3 = - 3 4.у4 = 4 5. у5 = - 1,5 | 1. у1 = 3х 2. у2 = 3х+1 3. у3 = 3х-2 4. у4 = 3х-1 5. у5 = 3х+2 |
2. Ответьте на вопросы:
a. Что общего вы видите в уравнениях?
b. Что общего вы видите в расположении прямых?
c. Какие можно сделать выводы?
| 1. Если а>0, то линейная функция возрастает Если а<0, то линейная функция убывает 2. Если в=0, то график функции у=ах проходит через начало координат. 3. Если а=0, то график функции прямая, параллельная оси абсцисс (х) 4. Если а=0 и в=0, график - ось абсцисс (х). 5. График функции у=ах+в можно получить из графика функции у=ах, сдвигая его по оси ординат на «в» единиц-вверх, если в˃0, вниз- если в˂0 |
Устно:
1. Среди данных функций назовите возрастающие, убывающие.
2. Графики каких функций проходят через начало координат?
3. Какие прямые образуют с осью х угол острый? тупой?
(Если угол –острый, то его тангенс больше 0 (известно из школьной программы), но k=tgα, поэтому к >0.
если угол –тупой, то его тангенс меньше 0, k=tgα<0).
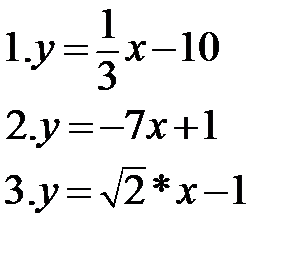 | 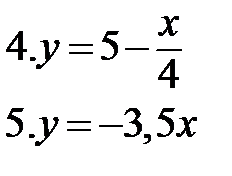 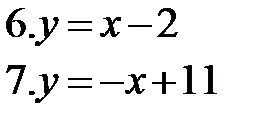 | 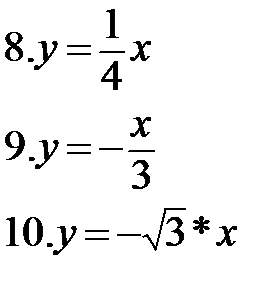 |
Самостоятельно:
Дана функция у=2х+1.
1. Постройте график функции.
2. Какие значения принимают аргумент х? функция у?
3. Какая это функция – возрастающая или убывающая?
4. В каких точках прямая пересекает ось абсцисс (у=0)? ось ординат?
5. Покажите ту часть графика, которая выше оси х. Какие значения принимает функция?
6. Покажите ту часть графика, которая ниже оси х. Какие значения принимает функция?
7. Чему равен тангенс угла наклона прямой к положительному направлению оси «х»?
Задача:
За 3 ч 20 мин пассажирский поезд прошел140 км, а автомобиль за 2 ч 10 мин прошел 156 км. Постройте графики движения поезда и автомобиля. Используя графики, ответьте на вопросы:
1) Сколько км прошел поезд за 1 ч 30 мин?
2) Сколько времени потребовалось автомобилю, чтобы пройти 120 км?
3) С какой скоростью шел поезд? автомобиль?
4) Во сколько раз скорость поезда больше скорости автомобиля?
5) Какое расстояние пройдет автомобиль за t часов?
Для удобства выберем масштаб: 1 клетка -10 единиц.
1. 3 ч20 мин=200мин, 2ч 10 мин=130 мин, 1ч30мин=90 мин.
Графиком этого движения является прямая, проходящая через начало координат. По условию поезд прошел за 200 минут 140 км- это вторая точка – (200;140)
По условию автомобиль прошел за 130 минут 156 км.
Получили графики:
S(км)
156 автомобиль
140
поезд
0 130 200 t(мин)
Пользуясь полученными графиками, получаем:
1. 63 км прошел поезд за 1 ч 30 мин
2. Чтобы пройти 120 км, автомобилю потребовалось 1 ч 40 минут.
3. Поезд шел со скоростью ≈42 км/ч, автомобиль ≈72 км/ч.
4. Скорость поезда больше скорости автомобиля в 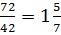 раза.
раза.
5. За t часов автомобиль пройдет 72 t км.
Квадратичная функция
На этих изумительных рисунках мы можем узнать знакомые математические силуэты. Какие?
Определение:
Квадратичной называется функция, имеющая вид:
у=ах2+bx+c, а≠ 0
где а, b, с - заданные числа, х –независимая действительная переменная – аргумент.
Графиком квадратичной функции является парабола.
Алгоритм построения параболы:
1. Определить направление ветвей параболы
Если а > 0, то «ветви» параболы направлены вверх  | Если а < 0, то «ветви» параболы направлены вниз |
2. Найти нули функции (точки пересечения параболы с осями координат):
у=0, ах2+bx+с=0, х1,2=…
х=0, у(0) = с.
3. Найти координаты вершины параболы:
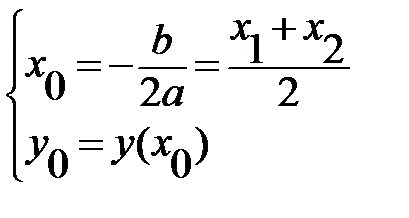
4. Провести ось симметрии
5*.Иногда вычисляют дополнительные точки.
Пример:
Построить график функции у=2х2+5х-3.
Решение
1. а=2˃0, следовательно, ветви направлены вверх.
2. Нули или точки пересечения с осями:
а) у=0, 2х2+5х-3=0, 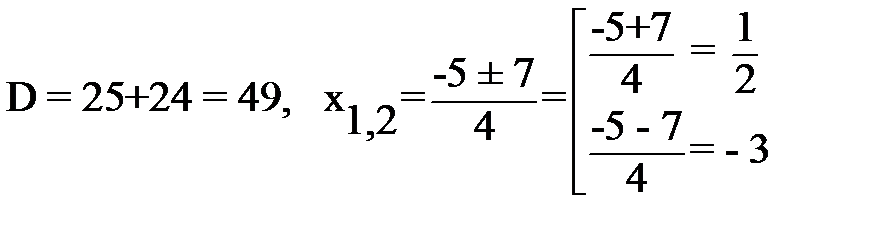
б) х=0, у(0)=-3.
3. Координаты вершины:
х0=- 1 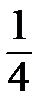 ,
,
у0=2( 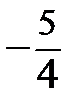 )2+5(
)2+5( 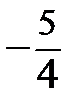 )-3=2
)-3=2 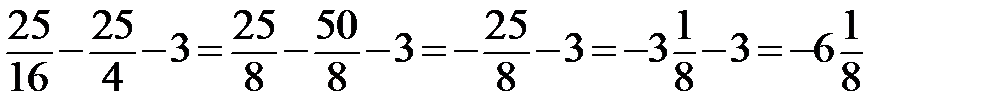 .
.
4. График:
Свойства:
1. у=0, если х = - 3 и х = 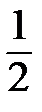 .
.
2. у≥0, если х≥ 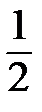 или х≤ - 3
или х≤ - 3
3. у˂0, если -3˂х˂ 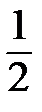
4. miny=-6,125, если х=-1,25.
5. Функция убывает от +∞ до - 6,125, если х 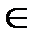 (-∞; -1,25]
(-∞; -1,25]
6. Функция возрастает от - 6,125 до +∞, если х 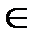 [--1,25;+∞)
[--1,25;+∞)
Выполните следующие задания:1.
| D>0,a>0 | |||||
| D>0,a<0 | |||||
| D<0,a>0 | |||||
| D<0,a<0 | |||||
| D=0,a>0 | |||||
| D=0,a<0 |
2.По графикам определите знаки а, b, с, D.
3.Укажите промежутки, на которых функция принимает положительные и отрицательные значения:
-2 2 -3 3
4.Укажите, при каких значениях «х» функция возрастает и убывает, принимает наибольшее значение и наименьшее.
| а |
| в |
| в |
5.Постройте графики функций:
a) у= - 2х2+6х-4 b) у = х2+4х c)у = х2+1 d)у = х2-2
Справка
 | Полезно вспомнить графики часто встречающихся функций! |
| у = ах3, а˃0 | у = 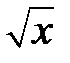 | ||||||
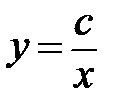 , с˃0 (ху=с˃0) , с˃0 (ху=с˃0) | 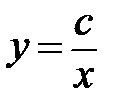 , с˂0 (ху=с˂0) , с˂0 (ху=с˂0) | ||||||
|
|
1.8.4.Индивидуальные задания
(Номер варианта равен остатку от деления номера по списку на количество вариантов). Значения a,b, c, d, m,n,t взять из таблиц.)
1.За «а» часов пассажирский поезд прошел b км, а автомобиль за c часов прошел d км. Постройте графики движения поезда и автомобиля. Используя графики, ответьте на вопросы:
1) Сколько км прошел поезд за m часов?
2) Сколько времени потребовалось автомобилю, чтобы пройти n км?
3) С какой скоростью шел поезд? автомобиль?
4) Во сколько раз скорость поезда больше скорости автомобиля?
5) Какое расстояние пройдет автомобиль за t часов?
| вариант данные | I. | II. | III. | IV. | V. | VI. | VII. |
| a (мин) | |||||||
| b (км) | |||||||
| c (мин) | |||||||
| d(км) | |||||||
| m(мин) | |||||||
| n (км) |
2.
1) Постройте график функции, заданной формулой у = ах+в.
2) Как изменяется переменная у (возрастает, убывает) с возрастанием переменной х?
3) Найдите множество значений х, при которых:
· у = 0
· у>0
· y<0.
4) Какой угол образует прямая с положительным направлением оси х (острый, тупой)?
5) Чему равен тангенс угла наклона прямой к лучу ох?
| вариант данные | I. | II. | III. | IV. | V. | VI. | VII. | VIII. |
| а | 2,4 | -2,4 | 2,4 | -2,4 | 1,2 | -1,2 | 1,2 | -1,2 |
| в | -3,6 | -3,6 | 3,6 | 3,6 | -1,8 | -1,8 | 1,8 | 1,8 |
3.Дана функция у =ax2+bx+c.
1. Найдите координаты точек пересечения графика с осями координат.
2. Построите график данной функции.
3. С помощью графика найдите:
a) множество значений х, при которых функция:
· возрастает
· убывает
· принимает положительные значения
· принимает отрицательные значения
b) значения переменной х, при которых функция принимает наибольшее или наименьшее значения.
4. Проходит ли график данной функции через точки A(m;n), B(-m;n), C(-m;-n), D(m;-n)?
| вариант данные | I. | II. | III. | IV. | V. | VI. | VII. | VIII. |
| a | -1 | -1 | -2 | 0,5 | -0,5 | |||
| b | -6 | -4 | -3 | -4 | -4 | |||
| c | -5 | -3 | -6 | -6 | ||||
| m | ||||||||
| n |
