Алгебра логики. Исчисление высказываний

Формулы алгебры логики

Высказыванием называется повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно. Например, высказывание “клён – дерево” истинно, а 3>5 – ложно.

Поставим в соответствие высказыванию Р логическую переменную х, которая принимает значение И (или 1), если Р истинно и Л (или 0), если Р ложно.

Рассматривания высказывания как величины, принимающие значения 1, 0, можно определить над ними операции, которые позволяют из одних высказываний получать новые.

Пусть даны два произвольных высказывания х и y.

1. Конъюнкцией называется высказывание х Ù y = х & y = х ∙ y = х y, которое истинно тогда и только тогда, когда х и y истинны.

2. Дизъюнкцией называется высказывание х Ú y, которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний х или y.

3. Импликация х ® y = х É y ложна тогда и только тогда, когда х – истина, а y – ложь. При этом х называется посылкой, а В – следствием (заключением).

4. Эквиваленция (эквивалентность) х ~ y =х « y истинна тогда и только тогда, когда и х, и y либо оба истинны, либо оба ложны.

5. Отрицание (инверсия) 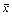= ù х истинно тогда и только тогда, когда х ложно.

В естественном языке конъюнкция соответствует соединению высказываний союзом «и», дизъюнкция – союзом «или» в неразделительном смысле.

Импликация х ® y выражается фразой «если х, то y» или «х влечет y», т.е. истинность х достаточна для того, чтобы у было истинным, а истинность y необходима для того, чтобы х было истинным.

Эквивалентность х ~ y в естественном языке читается «х тогда и только тогда, когда y» или «х является необходимым и достаточным для y».

Пусть x, y, z, ... – произвольные высказывания, т. е. величины, принимающие значения И и Л. Всякое сложное высказывание, составленное из них с помощью введенных операций алгебры высказываний называется формулой алгебры высказываний.

Пример 5.1. Формулами алгебры высказываний являются следующие выражения
( x®(y Ú z), 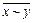, x Ú(y Ù z).

Функция, записанная с помощью переменных элементарных высказываний, принимает значения И или Л, в зависимости от значений аргументов. Поэтому для любой функции алгебры высказываний можно построить таблицу истинности.

Приведем таблицы истинности простейших функций:

Таблица 5.1

х	у	х Ù у	х Ú у	х ® у	х ~ у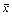
Л	Л	Л	Л	И	И	И
Л	И	Л	И	И	Л	И
И	Л	Л	И	Л	Л	Л
И	И	И	И	И	И	Л

Всякая формула задает способ вычисления функции, если известны значения переменных.

Пример 5.2.

Построим таблицу значений функции f(x₁, x₂, x₃) = ù (x₂ ®ù x₃) ~ (ù x₁Úx₂).

Таблица 5.2 представляет последовательное вычисление этой функции.

Таблица 5.2

x1	x2	x3	ù x3	x2 ®ù x3	ù (x2 ®ù x3)	ù x1	ù x1Úx2	f(x1, x2, x3)
Л Л Л Л И И И И	Л Л И И Л Л И И	Л И Л И Л И Л И	И Л И Л И Л И Л	И И И Л И И И Л	Л Л Л И Л Л Л И	И И И И Л Л Л Л	И И И И Л Л И И	Л Л Л И И И Л И

Таким образом, формула каждому набору аргументов ставит в соответствие значение функции. Следовательно, формула так же, как и таблица, может служить способом задания функции. В дальнейшем формулу будем отождествлять с функцией, которую она реализует. Последовательность вычислений функции задается скобками. Принято соглашение об опускании скобок в соответствии со следующей приоритетностью операций: ù, Ù, Ú, ® и ~.

Формула называется выполнимой, если существует такой набор значений переменных, при которых эта формула принимает значение “истинно”.

Формула называется тождественно истинной или тавтологией, если эта формула принимает значение “истинно” при всех наборах переменных.

Формула называется тождественно ложной, если эта формула принимает значение “ложно” при всех наборах переменных.

Функции алгебры логики

Как уже отмечалось выше значение логическое переменной «истина» принять обозначать «1», а «ложь» - «0».

Функцией алгебры логики или булевой функцией f(x₁, x₂, ... , x_n) называется произвольная функция n переменных, аргументы которой x₁, x₂, ... , x_n и сама функция f принимают значения 0 или 1, т. е. x_i 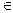{0, 1}, i = 1, 2, ... , n;
f(x₁, x₂, ... , x_n) 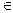{0, 1}.

Булевых функций двух переменных – 16 (2² 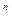при n = 2). Они представлены в таблице 5.3.

Таблица 5.3

x1

x2

0

x1&x2

f2

x1

f4

x2

x1 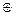x2

x1Úx2

x1¯x2

x1~x2

ùx2

x2®x1

ùx1

x1®x2

x1ïx2

1

0

1

1

Кроме уже введенных в п. 5.1 специальные названия имеют функции:

x₁ 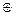x₂ – сложение по модулю два (исключающее «или», строгая дизъюнкция);

x₁¯x₂ – стрелка Пирса (антидизъюнкция);

x₁ï x₂ – штрих Шеффера (антиконъюнкция).

Эквивалентность формул

В отличие от табличного задания представление функции формулой не единственно. Например, две различные формулы ù x₁Úù x₂ и ù (x₁&x₂) реализуют одну функцию – штрих Шеффера.

Две формулы, реализующие одну и ту же функцию, называются равносильными.

Равносильность формул A и B будем обозначать следующим образом: A= B.

Для того, чтобы установить равносильность формул, можно составить таблицы значений функции для каждой формулы и сравнить их. Для равносильных формул эти таблицы совпадают. Другой способ установления равносильности формул заключается в использовании некоторых установленных равносильностей булевых формул.