Алгебра высказываний (алгебра логики).
Учение о высказываниях – — алгебра высказываний или алгебра логики является простейшей логической теорией. Она рассматривает конечные конфигурации символов и взаимоотношения между ними.
Высказывание – — это всякое повествовательное предложение, утверждающее что-либо о чем-либо, при этом непременно истинное или ложное. Логическими значениями высказываний являются “"истина”" и “"ложь”", обозначаемые 1 и 0. Высказывания, представляющие собой одно утверждение, называются простыми или элементарными, высказывания, получающиеся из элементарных с помощью грамматических связок “"не”", “"и”", “"или”", “"если… , то…”", называются сложными. Эти названия не носят абсолютного характера, высказывания, которые в одной ситуации можно считать простыми, в другой ситуации будут сложными. В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, житейское содержание игнорируется. Каждое высказывание может быть либо истинным, либо ложным, ни одно высказывание не может быть одновременно истинным и ложным. Элементарные высказывания обозначаются строчными буквами латинского алфавита: а, b, с. Из высказываний с помощью логических связок образуются новые высказывания. Рассмотрим наиболее употребительные логические связки.
Отрицанием высказывания  называется новое высказывание, которое является истинным, если высказывание
называется новое высказывание, которое является истинным, если высказывание  ложно, и ложным, если
ложно, и ложным, если  – — истинно. Обозначается
– — истинно. Обозначается 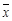 , читается “"не
, читается “"не  ”" или “"неверно, что
”" или “"неверно, что  ”". Все логические значения высказывания
”". Все логические значения высказывания 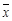 можно описать с помощью табл. 1.13. Если
можно описать с помощью табл. 1.13. Если 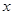 – — высказывание, то
– — высказывание, то 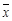 - — противоположное высказывание. Тогда можно образовать
- — противоположное высказывание. Тогда можно образовать 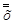 , которое называется двойным отрицанием высказывания. Логические значения
, которое называется двойным отрицанием высказывания. Логические значения 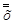 , очевидно, совпадают со значениями
, очевидно, совпадают со значениями  . Эта операция одноместная – — в том смысле, что из одного данного простого высказывания
. Эта операция одноместная – — в том смысле, что из одного данного простого высказывания  строится новое высказывание
строится новое высказывание 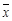 .
.
Логическое умножение (конъюнкция). Конъюнкцией двух высказываний  и
и  называется новое высказывание
называется новое высказывание 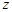 , которое истинно только когда оба высказывания
, которое истинно только когда оба высказывания  и
и  истинны, и ложно, когда хотя бы одно из
истинны, и ложно, когда хотя бы одно из  и
и  ложно. Обозначается
ложно. Обозначается 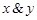 &
& 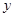 или
или 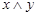 , читается “"
, читается “"  и
и  ”".Таблица истинности конъюнкции дана в табл. 1.14. Из определения операции конъюнкции видно, что союз “"и”" в алгебре логики употребляется в том же смысле, что и в повседневной речи. Однако в алгебре логики этой связкой можно связывать любые, сколь угодно далекие по смыслу высказывания. Конъюнкцию часто называют логическим умножением.
”".Таблица истинности конъюнкции дана в табл. 1.14. Из определения операции конъюнкции видно, что союз “"и”" в алгебре логики употребляется в том же смысле, что и в повседневной речи. Однако в алгебре логики этой связкой можно связывать любые, сколь угодно далекие по смыслу высказывания. Конъюнкцию часто называют логическим умножением.
Таблица 1.13 Таблица 1.14
 |  | 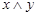 |
 | 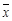 |
Логическое сложение (дизъюнкция).Дизъюнкцией двух высказываний  и
и  называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний
называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний  и
и  истинно, и ложным, если они оба ложны. Обозначается
истинно, и ложным, если они оба ложны. Обозначается 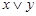 , читается “"
, читается “"  или
или  ”". Логические значения дизъюнкции описываются в табл.1.15.
”". Логические значения дизъюнкции описываются в табл.1.15.
Таблица 1.15 Таблица 1.16
 |  | 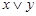 |
 |  | 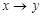 |
Импликация или логическое следование.Импликацией двух высказываний  и
и  называется новое высказывание, которое считается ложным, когда
называется новое высказывание, которое считается ложным, когда  истинно, а y ложно, и истинным во всех остальных случаях. Обозначается
истинно, а y ложно, и истинным во всех остальных случаях. Обозначается 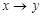 , читается “"если
, читается “"если  , то
, то  ”" или “"из
”" или “"из  следует
следует  ”". Высказывание
”". Высказывание  называется условием или посылкой, высказывание
называется условием или посылкой, высказывание 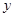 — следствием или заключением. Таблица истинности этой операции приведена в табл. 1.16. Из таблицы истинности видно, что если условие
— следствием или заключением. Таблица истинности этой операции приведена в табл. 1.16. Из таблицы истинности видно, что если условие  - — истинно, и истинна импликация
- — истинно, и истинна импликация 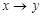 , то верно, и заключение
, то верно, и заключение  . Это классическое правило вывода, постоянно используется в математике, при переходе от одних высказываний к другим, с помощью доказываемых теорем, которые, как правило, имеют форму импликаций.
. Это классическое правило вывода, постоянно используется в математике, при переходе от одних высказываний к другим, с помощью доказываемых теорем, которые, как правило, имеют форму импликаций.
В случае импликации несоответствие между обычным пониманием истинности сложного высказывания и идеализированной точкой зрения алгебры высказываний еще заметнее, чем для других логических операций. Здесь истинность импликации в некоторой ситуации означает лишь, что если в этой ситуации истинна посылка, то истинно и заключение.
Эквиваленция (эквивалентность, логическая эквивалентность). Эквиваленцией двух высказываний  и
и  называется новое высказывание, которое истинно, когда оба высказывания
называется новое высказывание, которое истинно, когда оба высказывания  и
и  либо одновременно истинны, либо одновременно ложны, и ложно во всех остальных случаях. Обозначается
либо одновременно истинны, либо одновременно ложны, и ложно во всех остальных случаях. Обозначается 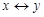 , читается “"для того, чтобы
, читается “"для того, чтобы  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  ”" или “"
”" или “"  тогда и только тогда, когда
тогда и только тогда, когда  ”". Эквивалентность играет значительную роль в математических доказательствах. Известно, что большое число теорем формулируется в форме необходимых и достаточных условий. Это так называемые теоремы существования. Логические значения операции эквиваленции описываются в табл. 1.17.
”". Эквивалентность играет значительную роль в математических доказательствах. Известно, что большое число теорем формулируется в форме необходимых и достаточных условий. Это так называемые теоремы существования. Логические значения операции эквиваленции описываются в табл. 1.17.
Таблица 1.17
 |  | 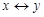 |
С помощью логических операций над высказываниями можно строить различные новые, более сложные высказывания. Всякое сложное высказывание, которое может быть получено из элементарных высказываний с помощью логических связок, называется формулой алгебры логики. Формулы алгебры логики обозначаются большими буквами латинского алфавита 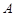 ,
, 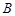 ,
, 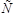 А, В, С,, … Две формулы алгебры логики
А, В, С,, … Две формулы алгебры логики 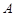 и
и 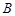 называются равносильными, если они принимают одинаковые логические значения при любом наборе значений, входящих в формулы элементарных высказываний. Равносильность обозначается знаком “" ≡ ”".
называются равносильными, если они принимают одинаковые логические значения при любом наборе значений, входящих в формулы элементарных высказываний. Равносильность обозначается знаком “" ≡ ”".
Для любых формул 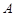 ,
, 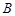 ,
, 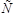
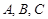 справедливы следующие равносильности.
справедливы следующие равносильности.
q I. Основные равносильности:
· 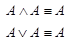 (законы идемпотентности конъюнкции и дизъюнкции);
(законы идемпотентности конъюнкции и дизъюнкции);
- законы идемпотентности конъюнкции и дизъюнкции,
· 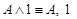 — истина;
— истина;
· 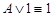 ;
;
· 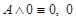 — ложь,
— ложь,
· 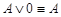 ;
;
· 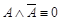 - (закон противоречия),; (1.13.1)
- (закон противоречия),; (1.13.1)
· 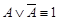 - (закон исключенного третьего,);
- (закон исключенного третьего,);
· 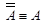 - (закон снятия двойного отрицания,);
- (закон снятия двойного отрицания,);
· 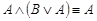 - (первый закон поглощения,);
- (первый закон поглощения,);
· 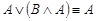 - (второй закон поглощения);,
- (второй закон поглощения);,
· 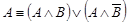 - (первая формула расщепления);,
- (первая формула расщепления);,
· 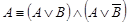 - (вторая формула расщепления)..
- (вторая формула расщепления)..
Все эти соотношения легко проверяются по таблицам истинности.
q II. Равносильности, выражающие одни логические операции через другие:
· 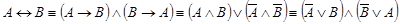 - (основная формула доказательств теорем существования);,
- (основная формула доказательств теорем существования);,
· 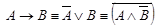 ;
;
· 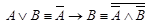 ,;
,;
· 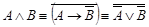 ;, (1.13.2)
;, (1.13.2)
· 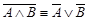 - (первый закон де Моргана)[4]*,;
- (первый закон де Моргана)[4]*,;
· 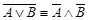 - (второй закон де Моргана);,
- (второй закон де Моргана);,
· 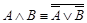 ;
;
· 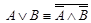 .
.
Именно из равносильностей этой группы формул следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логические операции: конъюнкцию и отрицание или дизъюнкцию и отрицание.
q III. Равносильности, выражающие основные законы алгебры логики:
· 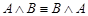 - (коммутативный закон конъюнкции);,
- (коммутативный закон конъюнкции);,
· 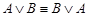 - (коммутативный закон дизъюнкции),;
- (коммутативный закон дизъюнкции),;
· 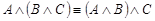 - (ассоциативность конъюнкции),; (1.13.3)
- (ассоциативность конъюнкции),; (1.13.3)
· 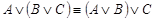 - (ассоциативность дизъюнкции);,
- (ассоциативность дизъюнкции);,
· 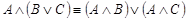 - (дистрибутивность конъюнкции относительно дизъюнкции,);
- (дистрибутивность конъюнкции относительно дизъюнкции,);
· 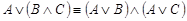 - (дистрибутивность дизъюнкции относительно конъюнкции).
- (дистрибутивность дизъюнкции относительно конъюнкции).
Формула 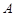 называется тождественно истинной или тавтологией, если она принимает значение 1 при всех значениях входящих в нее переменных. Формула
называется тождественно истинной или тавтологией, если она принимает значение 1 при всех значениях входящих в нее переменных. Формула 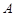 называется тождественно ложной или противоречивой, если она равна 0 при всех значениях входящих в нее переменных.
называется тождественно ложной или противоречивой, если она равна 0 при всех значениях входящих в нее переменных.
Формула алгебры логики является функцией входящих в нее элементарных высказываний, ее аргументы принимают два значения 0 и 1, при этом значение формулы может быть равно 0 или 1.
Функцией алгебры логики 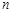 переменных (или функцией Буля) называется функция
переменных (или функцией Буля) называется функция 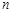 логических переменных, то есть функцией алгебры логики
логических переменных, то есть функцией алгебры логики 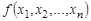 от
от 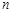 переменных
переменных 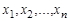 называется функция, принимающая значения 0, 1, аргументы которой также принимают значения 0, 1.
называется функция, принимающая значения 0, 1, аргументы которой также принимают значения 0, 1.
Функция 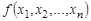 задается своей истинностной таблицей 1.18.
задается своей истинностной таблицей 1.18.
Таблица 1.18
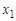 | 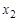 | … | 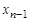 | 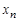 | 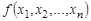 |
| … | 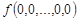 | ||||
| … | 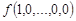 | ||||
| … | … | … | … | … | … |
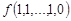 | |||||
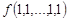 |
Из этой таблицы видно, что число различных двоичных наборов длины 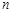
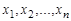 конечно и равно
конечно и равно 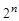 .
.
Ясно, что тавтологии и тождественно ложные функции алгебры логики представляют собой постоянные функции, а две равносильные формулы выражают одну и ту же функцию. Каждая функция определяется таблицей истинности, состоящей из 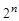 строк, то есть принимает
строк, то есть принимает 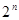 значений (каждое 0 или 1). Общее число наборов из 0 и 1 длины
значений (каждое 0 или 1). Общее число наборов из 0 и 1 длины 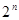 равно
равно 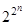 Это число равно числу различных функций алгебры логики
Это число равно числу различных функций алгебры логики 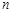 переменных.
переменных.
Каждой формуле алгебры логики соответствует своя функция. Если формулы 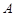 и
и 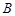 эквивалентны, то соответствующие им функции равны:
эквивалентны, то соответствующие им функции равны: 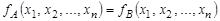 . Это значит, что при всех значениях переменных
. Это значит, что при всех значениях переменных 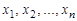 значения
значения 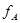 и
и 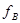 совпадают.
совпадают.
Каждая булева функция может быть путем эквивалентных преобразований приведена к двум особым формам, которые называются дизъюнктивной и конъюнктивной нормальными формами. Пусть 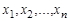 переменные булевой функции
переменные булевой функции 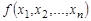 , а
, а 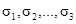 - — набор этих переменных. Введем обозначение:
- — набор этих переменных. Введем обозначение: 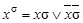 , где
, где 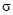 -— параметр, равный 0 или 1. Очевидно, что
-— параметр, равный 0 или 1. Очевидно, что 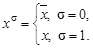 Тогда функцию
Тогда функцию 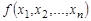 можно представить в виде:
можно представить в виде:
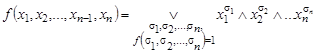 , (1.13.4)
, (1.13.4)
где дизъюнкция берется по всевозможным наборам значений переменных 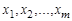 или
или
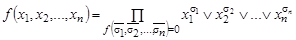 , (1.13.5)
, (1.13.5)
где символ 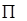 означает, что конъюнкции берутся по тем наборам переменных, которые указаны под ним. Нормальные формы позволяют дать критерий равносильности двух произвольных формул
означает, что конъюнкции берутся по тем наборам переменных, которые указаны под ним. Нормальные формы позволяют дать критерий равносильности двух произвольных формул 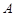 и
и 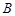 .
.
Аппарат булевых функций используется для проектирования цифровых устройств и базовых элементов компьютерных систем.
Элементы теории множеств.
Первичным понятием теории множеств является понятие самого множества. Множество – — это совокупность некоторых (произвольных) объектов, объединенных по какому-либо признаку. Элементы множества при этом должны быть различными. Множество обозначается парой скобок 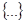 , внутри которых либо просто перечисляются элементы, либо описываются их свойства. Например,
, внутри которых либо просто перечисляются элементы, либо описываются их свойства. Например, 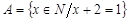 - — множество натуральных чисел, удовлетворяющих условию
- — множество натуральных чисел, удовлетворяющих условию 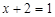 , очевидно, пусто.
, очевидно, пусто. 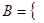 сложение, умножение
сложение, умножение 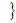 - — множество основных арифметических операций. Пустое множество обозначается знаком Æ. Если необходимо указать, что объект
- — множество основных арифметических операций. Пустое множество обозначается знаком Æ. Если необходимо указать, что объект 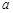 является элементом множества
является элементом множества 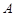 , то пишут
, то пишут 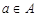 (
( 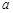 принадлежит
принадлежит 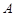 ), наоборот запись
), наоборот запись 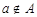 говорит о том, что
говорит о том, что 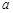 не принадлежит
не принадлежит  .
.
Если каждый элемент множества  является элементом множества
является элементом множества 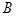 , то пишут
, то пишут 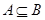 или
или 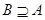 и говорят, что множество
и говорят, что множество  является подмножеством множества
является подмножеством множества 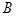 . Если
. Если  есть подмножество множества
есть подмножество множества 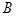 , причем
, причем 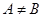 , то пишут
, то пишут 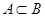 или
или 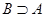 . Множества, состоящие из одних и тех же элементов, называются равными, то есть
. Множества, состоящие из одних и тех же элементов, называются равными, то есть 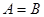 , в противном случае
, в противном случае 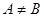 . С помощью скобок и операций над множествами можно построить новые множества, более сложные, чем исходные.
. С помощью скобок и операций над множествами можно построить новые множества, более сложные, чем исходные.
Объединение (или сумма). Эта операция над множествами обозначается 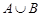 , определяется как
, определяется как 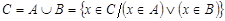 . Все операции над множествами можно иллюстрировать с помощью диаграмм Эйлера[5]*- Венна[6]**. Если за некоторое универсальное множество, содержащее как подмножества все другие множества, обозначить
. Все операции над множествами можно иллюстрировать с помощью диаграмм Эйлера[5]*- Венна[6]**. Если за некоторое универсальное множество, содержащее как подмножества все другие множества, обозначить 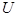 (или
(или 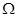 ) и изобразить его в виде всей плоскости, то любое множество
) и изобразить его в виде всей плоскости, то любое множество 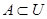 можно изобразить в виде части плоскости, то есть в виде некоторой фигуры, лежащей на плоскости. Множество
можно изобразить в виде части плоскости, то есть в виде некоторой фигуры, лежащей на плоскости. Множество 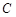 объединение множеств
объединение множеств 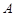 и
и 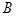 ,
, 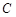 на рис. 1.7 заштриховано.
на рис. 1.7 заштриховано. 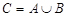 .
.
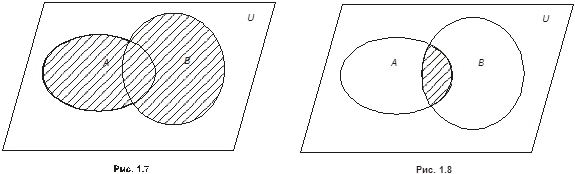 |
Рис. 1.7.Объединение множеств
Рис. 1.8.Пересечение множеств
Пересечением (или произведением)двух множеств называется такое множество 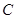 , которое состоит из элементов, принадлежащим одновременно обоим множествам, то есть
, которое состоит из элементов, принадлежащим одновременно обоим множествам, то есть 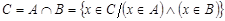 . Пересечение множеств
. Пересечение множеств  и
и 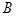 заштриховано и изображено на рис. 1.8.
заштриховано и изображено на рис. 1.8.
Разностью двух множеств  и
и 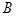 называется множество
называется множество 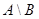 , состоящее из тех и только тех элементов, которые входят в
, состоящее из тех и только тех элементов, которые входят в  и одновременно не входят в
и одновременно не входят в 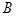 , то есть
, то есть 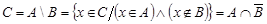 [K2] [S3] (см. рис. 1.9). Если, в частности,
[K2] [S3] (см. рис. 1.9). Если, в частности,  подмножество
подмножество 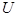 , то разность
, то разность 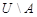 обозначается
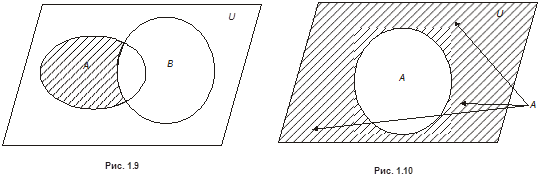
обозначается 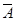 и называется дополнением множества
и называется дополнением множества  (см. рис . 1.10).
(см. рис . 1.10).
Рис. 1.9.Разность множеств
Рис. 1.10. Дополнение множества
 |
Симметрической разностью или кольцевой суммой множеств
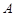 и
и 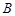 называется множество
называется множество 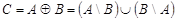 (см. рис . 1.11). Очевидно, что
(см. рис . 1.11). Очевидно, что 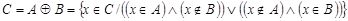 . Если
. Если 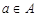 и
и 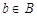 , то пару элементов
, то пару элементов 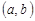 называют упорядоченной парой, причем пары
называют упорядоченной парой, причем пары 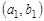 и
и 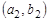 равны тогда и только тогда, когда
равны тогда и только тогда, когда 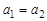 и
и 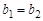 .
. 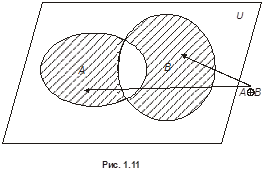
Рис. 1.11.Симметрическая разность
Множество, элементами которого являются все упорядоченные пары 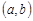 ,
, 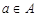 ,
, 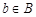 называется прямым или декартовым произведением множеств
называется прямым или декартовым произведением множеств  и
и 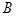 и обозначается
и обозначается 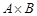 . Например,
. Например, 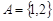 ,
, 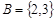
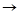
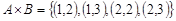 , а
, а 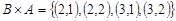 . Таким образом, декартово произведение не подчиняется коммутативному закону, и
. Таким образом, декартово произведение не подчиняется коммутативному закону, и 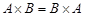 справедливо, если
справедливо, если 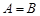 . Произведение
. Произведение 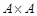 называется декартовым квадратом.
называется декартовым квадратом.
Свойства операций объединения, пересечения и дополнения иногда называются законами алгебры множеств. Эти законы аналогичны правилам для равносильностей в булевой алгебре (1.13.1) –—(1.13.3).
Часто элементы разных множеств связаны различными соотношениями, например, соотношениями порядка. 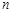 -местным отношением или
-местным отношением или 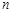 -местным предикатом
-местным предикатом 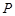 на множествах
на множествах 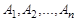 называется любое подмножество декартова произведения
называется любое подмножество декартова произведения 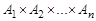 . Обозначение
. Обозначение 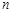 -местного отношения
-местного отношения 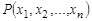 . При
. При 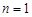 отношение
отношение 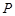 называется унарным и является подмножеством множества
называется унарным и является подмножеством множества 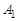 . Бинарным (или двуместным при
. Бинарным (или двуместным при 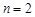 ) отношением называется множество упорядоченных пар. Элементы
) отношением называется множество упорядоченных пар. Элементы 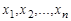 называются координатами или компонентами отношения
называются координатами или компонентами отношения 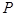 .
.
В теории множеств важную роль играют два вида специальных бинарных отношений: отношения эквивалентности и отношения порядка. Прообразами этих отношений служат интуитивные понятия равенства, предшествования и предпочтения.
Рассмотрим два конечных множества 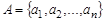 ,
, 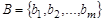 и бинарное отношение
и бинарное отношение 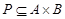 . Введем матрицу
. Введем матрицу 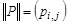 бинарного отношения
бинарного отношения 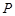 следующим образом:
следующим образом:
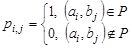 .
.
Эта матрица содержит полную информацию о связях между элементами множеств 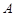 и
и 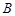 и позволяет представить эту информацию в графическом виде.
и позволяет представить эту информацию в графическом виде.
Матрица любого бинарного отношения обладает следующими свойствами:
q если 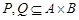 и
и 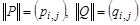 , то
, то 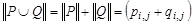 ;
; 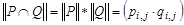 , причем сложение элементов матрицы осуществляется по правилам 0 + 0 = 0, 1 + 1 = 1, 1 + 0 = 0 + 1 = 1, а умножение осуществляется почленно обычным образом, т. е. по правилам
, причем сложение элементов матрицы осуществляется по правилам 0 + 0 = 0, 1 + 1 = 1, 1 + 0 = 0 + 1 = 1, а умножение осуществляется почленно обычным образом, т. е. по правилам 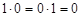 ,
, 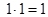 ;
;
q 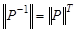 , где
, где 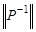 - — матрица обратного отношения
- — матрица обратного отношения 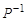 ;
;
q если 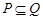 , то
, то 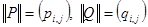 и
и 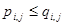 .
.
Пример 1.Бинарное отношение 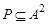 ,
, 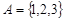 изображено на рис. 1.12. Его матрица имеет вид:
изображено на рис. 1.12. Его матрица имеет вид:
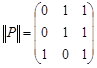 .
.
Пусть
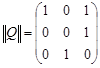 ,
,
тогда
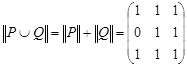 ,
, 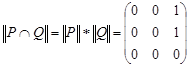 .
.
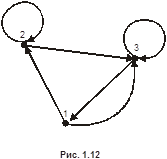
Рис. 1.12.Бинарное отношение 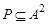 ,
, 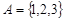
Пусть 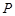 - — бинарное отношение на множестве
- — бинарное отношение на множестве 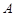 ,
, 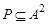 . Отношение
. Отношение 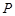 на множестве
на множестве 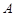 называется рефлексивным, если
называется рефлексивным, если 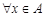 ,
, 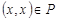 , т. е.
, т. е.
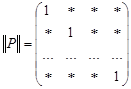 ,
,
где звездочкой обозначены нули или единицы. Отношение 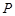 называется иррефлексивным, если
называется иррефлексивным, если 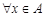 ,
, 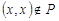 . Отношение
. Отношение 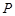 на множестве
на множестве  называется симметричным, если
называется симметричным, если 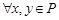 и, из условия
и, из условия 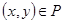 следует, что
следует, что 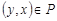 . Это значит, что
. Это значит, что 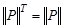 . Отношение
. Отношение 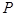 называется антисимметричным, если из условий
называется антисимметричным, если из условий 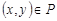 и
и 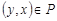 следует, что
следует, что 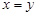 , или
, или 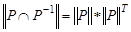 . Это свойство приводит к тому, что у матрицы
. Это свойство приводит к тому, что у матрицы 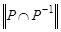 все элементы вне главной диагонали будут нулевыми (на главной диагонали тоже могут быть нули). Отношение
все элементы вне главной диагонали будут нулевыми (на главной диагонали тоже могут быть нули). Отношение 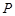 называется транзитивным, если из
называется транзитивным, если из 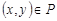 и
и 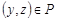 следует, что
следует, что 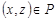 .
.
Рис. 1.12.Бинарное отношение 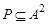 ,
, 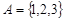
Рефлексивное, транзитивное и симметричное отношение на множестве 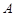 называется эквивалентностью на
называется эквивалентностью на 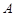 . Эквивалентность обозначается символами
. Эквивалентность обозначается символами 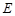 или ~, например,
или ~, например, 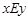 ,
, 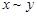 .
.
Пример 2. Докажем, что на множестве 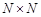 отношение
отношение 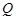 является отношением эквивалентности, если
является отношением эквивалентности, если 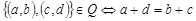 .
.
Если отношение 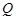 рефлексивно на
рефлексивно на 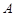 , то
, то 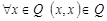 . В нашем случае роль
. В нашем случае роль 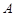 играет множество
играет множество 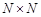 , а роль элемента
, а роль элемента  играет пара
играет пара 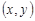 . Тогда отношение
. Тогда отношение 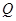 рефлексивно на
рефлексивно на 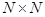 , если
, если 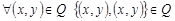 . По определению
. По определению 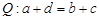 , но
, но 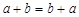 , следовательно,
, следовательно, 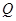 рефлексивно.
рефлексивно.
Аналогично, если 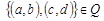 , то и
, то и 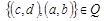 , так как из
, так как из 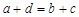 следует, что
следует, что 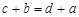 . Таким образом,
. Таким образом, 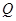 симметрично.
симметрично.
Наконец, если 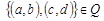 ,
, 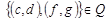 , то
, то 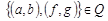 , так как
, так как 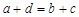 и
и 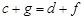 . Тогда
. Тогда 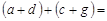
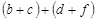
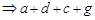
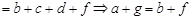 , т. е.
, т. е. 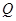 транзитивно.
транзитивно.
Рефлексивное, транзитивное и антисимметричное отношение на множестве  называется частичным порядком на
называется частичным порядком на  . Частичный порядок обозначается символом
. Частичный порядок обозначается символом 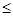 , а обратное ему отношение
, а обратное ему отношение 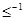 символом
символом 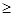 . Отношение
. Отношение 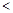 < называется строгим порядком и определяется таким образом:
< называется строгим порядком и определяется таким образом: 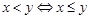 и
и 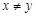 . Это отношение не является частичным порядком, так как не удовлетворяет условию рефлексивности
. Это отношение не является частичным порядком, так как не удовлетворяет условию рефлексивности 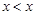 .
.
Если во множестве  есть элементы
есть элементы  и
и  , о которых нельзя сказать, что
, о которых нельзя сказать, что 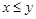 или
или 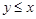 , то такие элементы называются несравнимыми. Частичный порядок называется линейным порядком, если любые два элемента
, то такие элементы называются несравнимыми. Частичный порядок называется линейным порядком, если любые два элемента  и
и  из множества
из множества  сравнимы, т. е.
сравнимы, т. е. 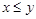 или
или 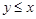 .
.
Непустое множество  , на котором зафиксирован некоторый частичный (линейный) порядок, называется частично (линейно) упорядоченным множеством. Элемент
, на котором зафиксирован некоторый частичный (линейный) порядок, называется частично (линейно) упорядоченным множеством. Элемент 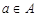 частично упорядоченного множества
частично упорядоченного множества  называется максимальным (минимальным), если для
называется максимальным (минимальным), если для 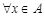 из того, что
из того, что 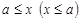 , следует
, следует 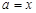 . Элемент
. Элемент 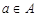 называется наибольшим (наименьшим), если
называется наибольшим (наименьшим), если 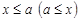 для всех
для всех 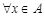 . Наибольший элемент обозначается
. Наибольший элемент обозначается 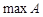 , наименьший - —
, наименьший - — 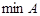 . Этих элементов у множества может и не быть, например, линейно упорядоченное множество рациональных чисел
. Этих элементов у множества может и не быть, например, линейно упорядоченное множество рациональных чисел 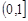 не имеет наименьшего элемента, наибольший элемент равен единице.
не имеет наименьшего элемента, наибольший элемент равен единице.
Верхней (нижней) гранью подмножества 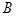 частично упорядоченного множества
частично упорядоченного множества  называется всякий элемент
называется всякий элемент 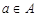 и такой, что
и такой, что 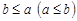 для всех
для всех 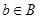 . Точной верхней (нижней) гранью подмножества
. Точной верхней (нижней) гранью подмножества 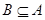 называется наименьшая верхняя (наибольшая нижняя) грань для
называется наименьшая верхняя (наибольшая нижняя) грань для 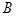 . Точная верхняя и точная нижняя грани множества
. Точная верхняя и точная нижняя грани множества 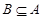 обозначаются через
обозначаются через 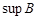 (супремум) и
(супремум) и 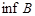 (инфимум) соответственно.
(инфимум) соответственно.
Линейный порядок 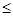 на множестве
на множестве  называется полным, если каждое непустое подмножество множества
называется полным, если каждое непустое подмножество множества  имеет наименьший элемент. В этом случае множество
имеет наименьший элемент. В этом случае множество  называется вполне упорядоченным.
называется вполне упорядоченным.
Элементы теории графов.
Граф задается парой множеств. Пусть 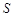 - — непустое множество,
- — непустое множество, 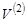 - — множество всех его двухэлементных подмножеств,
- — множество всех его двухэлементных подмножеств, 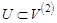 . Тогда пара
. Тогда пара 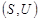 называется неориентированным графом.Элементы множества
называется неориентированным графом.Элементы множества 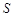 называются вершинами графа, а элементы множества
называются вершинами графа, а элементы множества 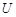 - — ребрами. Итак,
- — ребрами. Итак, 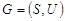 граф - — это конечное множество вершин
граф - — это конечное множество вершин 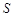 и множество ребер
и множество ребер 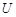 .
.
Вершины графа обозначают по-разному: или большими буквами, или малыми с индексами; для ребер наиболее употребительное обозначение - 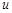 с индексом, например,
с индексом, например, 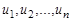 . Взаимное расположение, форма и длина ребер значения не имеют. Важно лишь то, что они соединяют две данные вершины множества
. Взаимное расположение, форма и длина ребер значения не имеют. Важно лишь то, что они соединяют две данные вершины множества 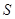 .
.
Если в паре вершин 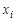 и
и 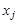 указано направление связи, т. е. какая из вершин является первой, то соединяющий их отрезок
указано направление связи, т. е. какая из вершин является первой, то соединяющий их отрезок 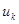 называется дугой, а вершины, определяющие дугу
называется дугой, а вершины, определяющие дугу 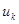 , называют концевыми вершинами. Если концевые вершины совпадают, то дугу называют петлей. В графе
, называют концевыми вершинами. Если концевые вершины совпадают, то дугу называют петлей. В графе 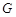 могут существовать дуги (ребра) с одинаковыми концевыми вершинами. Такие дуги называются параллельными.
могут существовать дуги (ребра) с одинаковыми концевыми вершинами. Такие дуги называются параллельными.
Если в графе 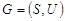 все элементы множества
все элементы множества 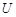 изображаются дугами, то граф называется ориентированным или орграфом, если ребрами, то неориентированным. Два ребра называются смежными, если они имеют общий конец.
изображаются дугами, то граф называется ориентированным или орграфом, если ребрами, то неориентированным. Два ребра называются смежными, если они имеют общий конец.
Вершина 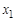 и ребро
и ребро 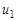 называются инцидентными, если
называются инцидентными, если 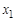 является концом ребра
является концом ребра 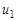 , и не инцидентными в противном случае. Таким образом, смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.
, и не инцидентными в противном случае. Таким образом, смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.
Число вершин графа называется его порядком. Степенью 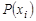 вершины
вершины 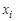 называется число дуг (ребер) графа
называется число дуг (ребер) графа 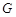 , инцидентных данной вершине. Вершина степени нуль называется изолированной, а если степень равна единице, то такая вершина называется висячей.
, инцидентных данной вершине. Вершина степени нуль называется изолированной, а если степень равна единице, то такая вершина называется висячей.
Граф 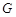 называется простымой, если он не содержит петель и параллельных дуг. Простой граф, в котором каждая пара вершин смежна, называется полным. Граф, содержащий хотя бы две параллельные дуги (ребра), — называется мультиграфом. Граф, содержащий петли, называется — псевдографом.
называется простымой, если он не содержит петель и параллельных дуг. Простой граф, в котором каждая пара вершин смежна, называется полным. Граф, содержащий хотя бы две параллельные дуги (ребра), — называется мультиграфом. Граф, содержащий петли, называется — псевдографом.
Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. Два графа 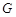 и
и 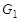 называются изоморфными, если между множеством их вершин существует такое взаимно однозначное соответствие, при котором в одном из графов ребрами соединены вершины в том и только в том случае, если в другом графе ребрами соединены те же вершины. Для орграфов ориентация дуг должна быть также одинаковой.
называются изоморфными, если между множеством их вершин существует такое взаимно однозначное соответствие, при котором в одном из графов ребрами соединены вершины в том и только в том случае, если в другом графе ребрами соединены те же вершины. Для орграфов ориентация дуг должна быть также одинаковой.
Очевидно, что отношение изоморфизма графов является эквивалентностью, т. е. оно симметрично, транзитивно и рефлексивно. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны.
Способов задания графов – — великое множество. Самый простой способ – — задание множеств 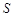 и
и 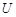 . Граф также может быть задан просто рисунком. В силу изоморфизма один и тот же граф может быть изображен разными рисунками.
. Граф также может быть задан просто рисунком. В силу изоморфизма один и тот же граф может быть изображен разными рисунками.
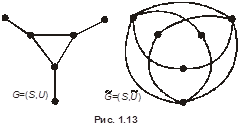
Рис. 1.13.Основной и Определение дополнительныйого графыа
Граф называется плоским (планарным), если он может быть изображен на плоскости так, что все пересечения ребер являются его вершинами. Для произвольного графа 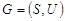 следующим образом определяется дополнительный граф (дополнение)
следующим образом определяется дополнительный граф (дополнение) 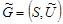 . В этом графе
. В этом графе 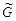 вершин столько же, сколько в графе
вершин столько же, сколько в графе 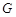 , причем любые две несовпадающие вершины смежны в
, причем любые две несовпадающие вершины смежны в 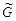 тогда и только тогда, когда они не смежны в
тогда и только тогда, когда они не смежны в 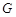 (см. рис. 1.13).
(см. рис. 1.13).
Чередующая последовательность 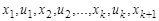 вершин и ребер графа, такая что
вершин и ребер графа, такая что 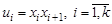 , называется маршрутом, соединяющим вершины
, называется маршрутом, соединяющим вершины 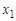 и
и 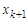 . Очевидно, что маршрут можно задать последовательностью его вершин
. Очевидно, что маршрут можно задать последовательностью его вершин 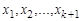 или последовательностью ребер
или последовательностью ребер 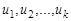 . Маршрут называется цепью, если все его ребра различны, и простой цепью, если все его вершины, кроме, возможно, крайних, различны. Гамильтоновой цепью называется простая цепь, содержащая все вершины графа.
. Маршрут называется цепью, если все его ребра различны, и простой цепью, если все его вершины, кроме, возможно, крайних, различны. Гамильтоновой цепью называется простая цепь, содержащая все вершины графа.
Маршрут называется циклическим, если 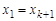 . Циклическая цепь называется циклом, а циклическая простая цепь – — простым циклом. Число ребер в маршруте — называется длинойа маршрута. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа. Длина всякого цикла не менее трех в графе без петель и кратных ребер. Минимальная из длин циклов графа называется его обхватом.
. Циклическая цепь называется циклом, а циклическая простая цепь – — простым циклом. Число ребер в маршруте — называется длинойа маршрута. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа. Длина всякого цикла не менее трех в графе без петель и кратных ребер. Минимальная из длин циклов графа называется его обхватом.
Важным понятием теории графов является связность. Граф называется связным, если любые две его несовпадающие вершины соединены маршрутом.

Рис. 1.14.Граф
В подавляющем большинстве случаев граф задается матрицей. Для расчетов на ЭВМ это единственный способ. Наиболее часто граф задают с помощью матриц смежности и инциденций.
Рассмотрим изображенный на рисунке . 1.14 граф. Как для орграфов, так и для неориентированных графов можно определить матрицу смежности вершин. Это квадратная матрица
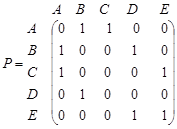
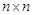 порядка, где
порядка, где 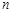 - — число вершин. Ее строки и столбцы соответствуют вершинам графа. Элементы
- — число вершин. Ее строки и столбцы соответствуют вершинам графа. Элементы 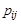 матрицы смежности вершин равны числу дуг, идущих из
матрицы смежности вершин равны числу дуг, идущих из 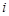 - той вершины в
- той вершины в
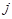 -ю вершину. Если орграф не содержит параллельных дуг, то матрица является бинарной и состоит только из нулей и единиц. В случае неориентированного графа ему вместе с ребром
-ю вершину. Если орграф не содержит параллельных дуг, то матрица является бинарной и состоит только из нулей и единиц. В случае неориентированного графа ему вместе с ребром 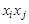 принадлежит и ребро
принадлежит и ребро 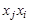 , поэтому матрица смежности вершин будет симметрической. Матрица смежности вершин однозначно определяет структуру графа. Аналогично можно определить и матрицу смежности дуг.
, поэтому матрица смежности вершин будет симметрической. Матрица смежности вершин однозначно определяет структуру графа. Аналогично можно определить и матрицу смежности дуг.
