Правило суммы. Правило произведения

Рассмотрим задачу определения мощности объединения n конечных множеств. Пусть n = 2 и A и B – два пересекающихся множества. Докажем с помощью диаграммы Эйлера – Венна следующее соотношение:

çАÈB ç= çА ç+ çB ç– çАÇB ç. (3.1)

Из рис. 3.1 видно, что çАÈB ç= n₁+n₂+n₃; çА ç= n₁+n₂; çB ç= n₂+n₃; çАÇB ç= n₂.

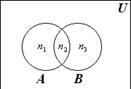
Рис. 3.1

Очевидно, что n₁+n₂+n₃ = (n₁+n₂) +(n₂+n₃) – n₂, что и доказывает формулу (3.1).

Пример 3.1. Сколько человек в группе занимается спортом, если 18 человек занимается лыжами, 11 человек – плаванием, а 5 человек – и лыжами и плаванием.

Решение. Обозначим А – множество тех, кто занимается лыжами, В – множество тех, кто занимается плаванием. Тогда по условию задачи n(A)=18, n(B)=11, n(AÇB)=5. Имеем: n(AÈB)=n(A)+n(B)- n(AÇB)=18+11-5=24. Ответ. 24 человека.

Формула (3.1) справедлива и для случая, если множества A и B не пересекаются. В этом случае çАÈB ç= çА ç+ çB ç.

Пусть n = 3 и A, B и С – три пересекающихся множества. В этом случае справедливо следующее соотношение:

çАÈBÈ Сç= çА ç+ çB ç+ çC ç– çАÇB ç– çАÇC ç– çBÇC ç+ çАÇB ÇC ç. (3.2)

Соотношение (3.2) проиллюстрировано на рис. 3.2.

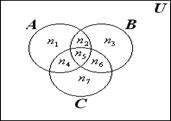
Рис. 3.2

Пример 3.2. Сколько из первых 100 натуральных чисел не делится ни на одно из чисел 2, 3 и 5?

Решение. Обозначим через U множество всех натуральных чисел не превышающих 100; через А, В и С – множества чисел из U, кратных соответственно двум, трем – и пяти; а через D – множество чисел из U, не делящихся ни на одно из этих чисел. Ясно, что D ÈA ÈB È C= U, причем D Ç (A È B È C) = Æ.

Используем обозначение: [a] – целая чисть числа a – наибольшее целое число не превосходящее a. По условию задачи имеем:

n(A)= 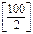= 50, n(B)= 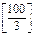= 33, n(C)= 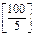= 20, n(A Ç B)= 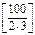= 16,
n(A Ç C)= 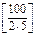= 10, n(BÇ C) = 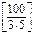= 6, n(A Ç B Ç C) = 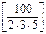= 3.

По формуле (3.2) получаем, что

n(A È B È C) = n(A) + n(B) + n(C) + n(A Ç B) - n(A Ç C) - n(B Ç C) + n(A Ç B Ç C)=
= 50 + 33 + 20 - 16 - 10 - 6 + 3 = 74,

и потому n(D) = n(U) - n(A È B È C) = 100 - 74 = 26

Ответ. 26 чисел.

Правило декартова произведения множеств А и В (см. п. 1.3) можно распространить и на комбинаторику: если элемент α можно выбрать k способами (n(A)=k), а элемент β - m способами (n(B)=m), то пару áα, β ñ можно выбрать k∙m способами. Это утверждение называют правилом произведения. Коротко его можно записать следующим образом:

n(A´B)=n(A)∙n(B).

Правило произведения может быть обобщено на случай конечного семейства множеств.

Для любых конечных множеств Х₁, Х₂, …Х_k имеет место равенство

n(Х₁´ Х₂´ …´ Х_k )= n(Х₁)× n(Х₂)× …× n(Х_k ).

Пример 3.3. Из города А до города В можно добраться пароходом, поездом, автобусом и самолетом; из В в С – пароходом и автобусом; а из С в N – пешком, на автомобиле или верхом на лошади. Сколькими способами можно осуществить путешествие по маршруту A – N ?

Решение. Обозначим А – множество возможностей для участка пути A – В; В - для участка пути В – С; С - для участка пути С – N. Тогда по условию задачи n(A)=4, n(B)=2, n(С)=3. По правилу произведения имеем: n(А´ В´ С)= n(А)× n(В)× n(С)=
=4× 2× 3 =24. Ответ. 24 способами.

Перестановки

Перестановками называют комбинации, состоящие из одних и тех же элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок из n элементов обозначается

P_n = n!=1×2×3×…×(n-1)×n

Пример 3.4. Сколькими способами шесть человек могут встать в очередь к кассе?

Решение. Так как каждому способу расстановки в очередь соответствует перестановка из восьми элементов, число способов будет перестановками без повторений. Следовательно: P₆ = 6!=1×2×3×4×5×6= 720.

Если некоторые из имеющихся n элементов повторяются, то в этом случае комбинации с повторениями называют перестановками с повторениями. Например, если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., то число перестановок с повторениями

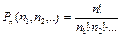, где n₁ + n₂ + … = n.

Пример 3.5. Требуется составить расписание отправления поездов на различные дни недели. При этом необходимо, чтобы: 3 дня отправлялись по 2 поезда в день, 2 дня – по 1 поезду в день, 2 дня – по 3 поезда в день. Сколько можно составить различных расписаний?

Решение. Количество поездов, отправляемых в день (числа 1,2,3), – это три группы одинаковых элементов, из которых должна быть составлена выборка. При этом в расписании на неделю число 1 повторяется 2 раза, число 2 повторяется 3 раза и число 3 повторяется 2 раза. Число различных расписаний равно

P₇(2,3,2)= 7!/(2!∙3!∙2!)=210.

Размещения

Размещением (без повторения) называются такие комбинации элементов, которые отличаются между собой или самими элементами или порядком их расположения в группе. Число всех размещений из n элементов по m обозначается 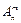и определяется по формуле: .

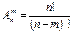Пример 3.6. Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан выбор, если каждый член общества может занимать лишь один пост?

Решение. В данном случае надо найти число размещений (без повторений) из 25 элементов по 4. Ведь здесь играет роль и то, кто будет выбран в руководство общества, и то, какие посты займут выбранные. Поэтому ответ дается формулой

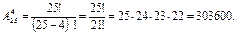
Размещением с повторениями называются такие комбинации элементов, которые отличаются между собой порядком их расположения в группе. Число всех размещений с повторениями из n элементов по m обозначается 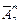и определяется по формуле: .

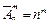Пример 3.7. Сколькими способами можно разделить 6 различных конфет между тремя детьми?

Решение. Каждый способ раздела является отображением множества конфет в множество детей. Число таких отображений равно 3⁶, т.е. 729.

Сочетания

Сочетанием называются такие комбинации элементов, которые отличаются между собой в каждой группе только самими элементами (но не порядком их расположения в группе). Если элементы не повторяются, то число сочетаний из n элементов по m обозначается 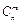и определяется по формуле:

.

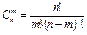Пример 3.8. Сколькими способами можно выбрать 5 делегатов из состава конференции на которой присутствуют 15 человек?

Решение. Так как порядок выбора значения не имеет и делегаты не повторяются, то число способов будет сочетаниями без повторений. Значит

.

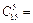
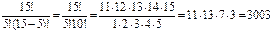Если же выбранные элементы могут повторяются, то число сочетаний с повторениями из n элементов по m обозначается 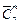и определяется по формуле:

.

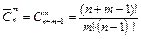Пример 3.9. Сколько наборов из 7 пирожных можно составить, если в продаже имеются 4 сорта пирожных?

Решение. Т.е. элементов (видов пирожных) 4: n=4. Из них выбирают 7 предметов для покупки: m=7. При этом порядок выбора элементов не важен и в комбинацию могут входить повторяющиеся элементы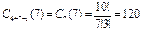

Пример 3.10. Сколькими способами можно разделить 6 одинаковых конфет между тремя детьми?

Решение. Поскольку конфеты одинаковые, то элементов (детей) n=3. Из них выбирают 6 раз того, кому дадут конфету: m=6. .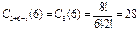

Примеры тестовых заданий

ЗАДАНИЕ N 3.1 ( - выберите один вариант ответа)
Количество элементов множества 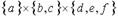равно …

ВАРИАНТЫ ОТВЕТОВ:

1)

2)

3)

4)

Решение. Число элементов в декартовом произведении множеств равно произведению числа элементов в этих множествах, т.е. 1∙2∙3=5. Верный ответ 3).

ЗАДАНИЕ N 3.2 ( - выберите один вариант ответа)
В группе 20 студентов. Тогда число способов выбрать среди них старосту и его заместителя, равно …

ВАРИАНТЫ ОТВЕТОВ:

1)

2)

3)

4)

Решение. Поскольку студенты выбираются на различные должности – то это размещения из 20 по 2: 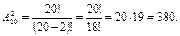Верный ответ 2).

ЗАДАНИЕ N 3.3 ( - введите ответ)
Число способов выбрать из группы в 20 студентов двух дежурных равно …

ВАРИАНТЫ ОТВЕТОВ:

Решение. Поскольку студенты выбираются на различные должности – то это сочетания из 20 по 2: 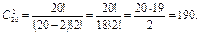Верный ответ 2).

ЗАДАНИЕ N 3.4 ( - выберите один вариант ответа)
Из ящика, где находится 15 деталей, пронумерованных от 1 до 15, требуется вынуть 3 детали. Тогда количество всевозможных комбинаций номеров вынутых деталей равно

ВАРИАНТЫ ОТВЕТОВ:

1)

15!

2)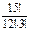

3)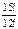

4)

3!

Решение. Поскольку детали пронумерованы– то это размещения из 15 по 3: 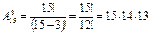. Верный ответ 3).

Графы