Вариационный принцип гамильтона

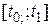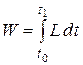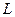Пусть задан промежуток времени , на котором исследуется движение консервативной системы. Выражение , где - функция Лагранжа, называется действием по Гамильтону. Размерность этой величины 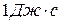. Значение величины 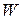зависит от того, какие функции 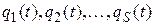(и, следовательно, какие функции 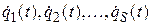) входят в выражение для 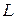. Действие по Гамильтону представляет собой отображение набора функций 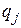на множество действительных чисел и называется функционалом. Функционал можно считать функцией от функции, в рассматриваемом случае – функцией от 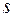функций .

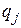Набор функций 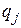условно называется путем системы. При движении системы реализуется путь, называемый прямым (на рис. 16 он изображен жирной линией). Другие пути, образующиеся благодаря варьированию величин 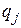в каждой точке 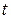, называются окольными. Окольные пути начинаются и заканчиваются в тех же точках пространства 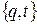, что и прямой путь.

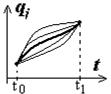
Рис. 16. Прямой путь и окольные пути

Принцип Гамильтона заключается в утверждении, что прямой путь отличается от окольных путей тем, что на нем действие принимает экстремальное (стационарное) значение. Экстремальное значение функционал приобретает при условии обращения в нуль его вариации, т.е. на прямом пути .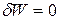

Действительно,

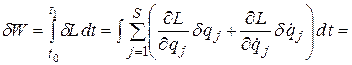
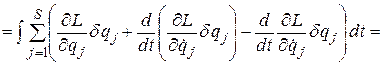
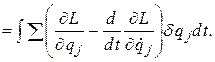
При этом 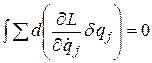, т.к. в начальной и конечной точках все пути сходятся: в этих точках 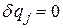. В силу уравнений Лагранжа-2 получаем .

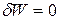*4.3.5. Уравнения Гамильтона

Введем вместо лагранжевых переменных 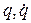гамильтоновы переменные 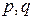. Здесь 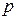- вектор обобщенных импульсов, определяемых формулами

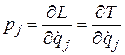
(потенциальная энергия зависит от переменных 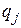и не зависит от 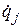). Тогда каждое уравнение Лагранжа-2 можно записать так:

.

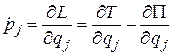Пусть связи стационарны: 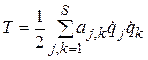; тогда справедливо равенство 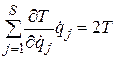, или .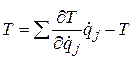

Отсюда получим

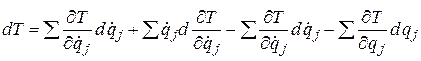или, с учетом введенных величин ,

.

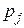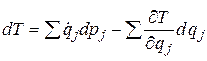С другой стороны, выражения 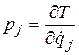представляют собой линейную систему уравнений относительно 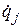, определитель которой 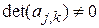(предложение п. 4.3.3). Тогда существует единственное нетривиальное (ненулевое) решение этой системы, и величины 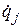можно выразить через 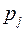и подставить в кинетическую энергию 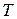, представив ее как функцию гамильтоновых переменных

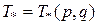
Отметим, что 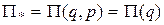). Имеем далее

.

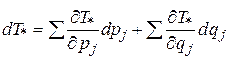Поскольку 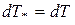, получаем, что

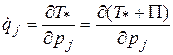и .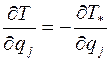

Тогда .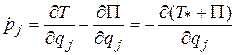

Функцию 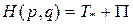называют функцией Гамильтона. При стационарных связях она есть полная механическая

энергия 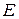системы, выраженная в гамильтоновых переменных.

Функцию Гамильтона можно представить также в виде:

.

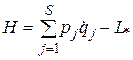Систему 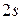дифференциальных уравнений первого порядка относительно функци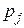й и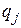

,

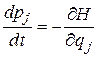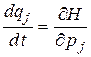
называют каноническими уравнениями Гамильтона движения консервативной системы.

4.3.6.* Циклические координаты

Обобщенная координата 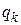называется циклической, если она явно не входит в выражение функции Лагранжа, т. е. если 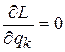. Тогда 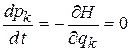, откуда следует

,

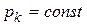т. е. имеем один из интегралов системы дифференциальных уравнений движения.

4.4. Малые колебания консервативной системы вблизи положения устойчивого равновесия