Простейшие действия с матрицами
1) Транспонирование.
Матрица  называется транспонированной по отношению к матрице А, если строки одной матрицы являются столбцами другой и наоборот, например,
называется транспонированной по отношению к матрице А, если строки одной матрицы являются столбцами другой и наоборот, например,
 .
.
2) Сложение (вычитание) матриц.
Чтобы найти сумму или разность двух матриц, нужно сложить или вычесть соответствующие элементы этих матриц, например,

 ;
;
 .
.
Замечание: исходя из определения, складывать или вычитать можно только матрицы одного размера.
3) Умножение на число (скаляр).
Чтобы умножить матрицу на число, нужно все ее элементы умножить на это число, например,
 .
.
Следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы.
Умножение матриц
Матрица С называется произведением матрицы А на матрицу В, если ее элементы вычисляются следующим образом:
 .
.
Т.е. элемент матрицы С, стоящий в 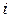 -той строке и
-той строке и 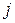 -том столбце, равен сумме произведений соответствующих элементов
-том столбце, равен сумме произведений соответствующих элементов 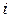 -той строки матрицы А и
-той строки матрицы А и 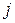 -того столбца матрицы В (соответствующих — это значит, что первый элемент строки умножаем на первый элемент столбца, второй — на второй и так до последней пары элементов).
-того столбца матрицы В (соответствующих — это значит, что первый элемент строки умножаем на первый элемент столбца, второй — на второй и так до последней пары элементов).
Из определения данного действия следует, что умножать можно только такие матрицы, в которых число столбцов матрицы А (т.е. число элементов в ее строке) равно числу строк матрицы В (т.е. числу элементов в ее столбце). Такие матрицы называются согласованными для умножения. Из определения умножения можно также заключить, что умножение матрицы А размера 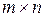 на матрицу В размера
на матрицу В размера  дает матрицу С размера
дает матрицу С размера  .
.
Заметим, что квадратные матрицы одного порядка всегда согласованы для умножения.
Пример.
 .
.
 .
.
Для данных матриц обратное умножение В на А невозможно, т.к. число столбцов в В равно 2, а число строк в матрице А равно 4. Но даже, если возможны оба произведения, они в общем случае могут не совпадать. Проверим:
 ;
;
 ;
;
 .
.
Свойства умножения матриц
1) В общем случае  , т.е. в общем случае перестановочное свойство умножения не выполняется.
, т.е. в общем случае перестановочное свойство умножения не выполняется.
Матрицы, для которых оно выполняется, называются перестановочными.
2) Сочетательное свойство:  .
.
3) Распределительное свойство умножения относительно сложения:

4) Умножение на единичную матрицу не меняет матрицы:  .
.
5) Умножение на нулевую матрицу дает нулевую матрицу:  ;
;
замечание: из того факта, что произведение двух матриц равно 0, не следует обязательно, что либо одна из них, либо обе вместе равны 0.
Матричные уравнения
Используя различные действия с матрицами, можно составлять матричные уравнения — соотношения между неизвестной матрицей Х и известными матрицами.
Например, АХ = В или ХА = В, АХВ = С, АХ + В = С, ХА — В = С и т.д.
Рассмотрим одно из простейших матричных уравнений:
 .
.
В школьном курсе алгебры рассматривалось соответствующее ему уравнение для действительных чисел:

Решением этого линейного уравнения является  , где число
, где число  называется обратным к
называется обратным к  и удовлетворяет соотношению:
и удовлетворяет соотношению:  .
.
Введем подобное понятие и для матриц. Матрица  называется обратной к
называется обратной к  , если она удовлетворяет условию:
, если она удовлетворяет условию:
 ,
,
где  — единичная матрица.
— единичная матрица.
Из определения обратной матрицы следует, что ее можно найти только для квадратных матриц.
Существование обратной матрицы дает возможность решать матричные уравнения, например, рассмотрим уравнение  . Умножим обе части уравнения слева на матрицу, обратную
. Умножим обе части уравнения слева на матрицу, обратную  :
:
 .
.
Аналогично можно найти решение уравнения  , умножая теперь уже справа обе части уравнения на
, умножая теперь уже справа обе части уравнения на  :
:
 .
.
