Тема 3. Дифференциальное исчисление
Согласовано
Методическим Советом
Протокол № ____
от «____» _______ 2014г.
Одобрено
Цикловой комиссией
Математических и общих
естественнонаучных дисциплин
протокол № __
от «___» ______________ 2013 г
Утверждаю
Зам. директора
По учебной работе
_____________ Коротаева Т.М.
«______» ______ _______ 2014г
Авторы:
Трудова С.В. – методист УТЖТ – филиала ПГУПС
рецензенты:
Коснырева Н.И. –преподаватель УТЖТ – филиала ПГУПС
пояснительная записка
Учебным планом специальностей 210420 Техническая эксплуатация технического транспортного радиоэлектронного оборудования (по видам транспорта) предусмотрена дисциплина «Прикладная математика».
«Прикладная математика» - обязательная дисциплина в цикле математических и общих естественнонаучных дисциплин. Изучение дисциплины позволяет приобрести знания необходимые для дальнейшего обучения в техникуме.
В результате изучения дисциплины студент должен иметь представление:
o о месте и роли математики в современном мире, общности ее понятий и представлений;
o о методах и средствах сбора, обработки, хранения, передачи и накопления информации;
o о методах математического моделирования и технологии решения задач с использованием ЭВМ;
o об информационной среде и тенденциях ее развития на железнодорожном транспорте;
знать и уметь использовать:
o математическую символику для выражения количественных и качественных отношений объектов;
o математические методы при решении прикладных задач; простые математические модели систем и процессов в сфере профессиональной деятельности;
o методы и средства информационных технологий при решении профессиональных задач;
иметь опыт:
o использования вычислительной техники и программного обеспечения применительно к профессиональной деятельности.
В процессе изучения дисциплины студент-заочник должен выполнить одну контрольную работу.
Данные методические указания ставят своей целью оказание помощи студентам-заочникам в организации их самостоятельной работы, содержат разъяснения некоторых теоретических положений для решения примеров и задач, способов их решения, вопросы для самопроверки, задания на контрольную работу.
Рекомендуется следующая последовательность изучения материала:
1. Ознакомиться с содержанием программы.
2. Изучить материал по указанной в методических указаниях литературе.
3. Ответить на вопросы для самопроверки.
4. Закрепить усвоение материала путем разбора решенных задач в данных методических указаниях, на практических занятиях, в учебнике.
5. Приступить к решению задач контрольной работы, предварительно изучив материал, касающийся содержания задач.
В целях закрепления знаний и приобретения необходимых навыков программой предусмотрены практические занятия, конкретное число которых определяет цикловая комиссия колледжа. Ниже приведен перечень практических занятий.
ЛИТЕРАТУРА
1. Богомолов Н.В. Практические занятия по математике. М., 2007.
2. Богомолов Н.В. Учебник. Математика. М., 2007
3. Дадаян А.А. Математика. М., 2003 г.
4. Брадис В.М. Четырехзначные математические таблицы (любое издание).
Общие методические указания
Данное пособие ставит своей целью оказание помощи студентам-заочникам в организации их самостоятельной работы по овладению системой знаний, умений и навыков в объеме действующей программы.
Эта работа требует не только большого упорства, но и умения, без которого затрата сил и времени не дает должного эффекта. Читать, понимать прочитанное и применять его практически – вот в чем суть умения работать с учебными пособиями.
Некоторые практические советы. Прежде всего, необходимо ознакомиться с содержанием программы. Затем следует выбрать в качестве основного учебное пособие и придерживаться его при изучении всей части курса, так как замена учебника может привести к утрате логической связи между отдельными вопросами.
Конспект по математике главным образом должны содержать определения, чертежи и выводы основных формул. Записи должны быть аккуратными. Не нужно забывать, что они делаются для того, чтобы впоследствии ими пользоваться.
Учитесь самоконтролю. Для заочника это важнейшая форма проверки правильности понимания и усвоения материала.
Помните: учебник нужно не читать, а изучать; основой запоминания является понимание, знание забывается – понимание никогда; повторение – важнейшее средство, предотвращающее забывание; необходимо вырабатывать привычку систематической самостоятельной работы, «натаскивание» к экзамену дает слабые и поверхностные знания.
О решении задач. Решение задач является лучшим способом закрепления материала. Конечно, общих рецептов для решения разнообразных задач не существует, однако рекомендуем придерживаться следующих советов:
1. Величины, данные в условии задачи, необходимо перевести в одну систему единиц; нарушение этого правила является распространенным источником ошибок у студентов.
2. Внимательно изучите цель, поставленную в задаче; выявите, какие теоретические положения связаны с данной задачей в целом или с некоторыми ее элементами.
3. Не следует приступать к решению задачи, не обдумав условия и не найдя плана решения.
4. Попытайтесь соотнести данную задачу к какому-либо типу задач, способ решения которых вам известен.
5. Если не видно сразу хода решения, то последовательно отвечайте на вопросы: что дано; что нужно найти; достаточно ли данных, чтобы найти неизвестное, и т. п.
6. Попробуйте расчленить данную задачу на серию вспомогательных, последовательное решение которых может составить решение данной задачи.
7. Найдя план решения, выполните его, убедитесь в необходимости и правильности каждого шага, произведите проверку решения и, если нужно, его исследование.
8. Подумайте, нельзя ли было решить задачу иначе; известно, что одна и та же задача может иметь несколько решений, поэтому следует выделить наиболее рациональное.
9. Если решить задачу не удается, отыщите в учебной (или популярной) литературе уже решенную задачу, похожую на данную, изучите внимательно это «готовое» решение и постарайтесь извлечь из него пользу для решения своей задачи.
Контрольные работы следует выполнять самостоятельно и лишь после того, как проработан соответствующий теоретический материал и решен необходимый минимум задач. Так как каждой теме соответствует задача или упражнение, то контрольную работу следует выполнять постепенно по мере изучения материала.
При решении задач следует обосновать каждый шаг решения, исходя из теоретических основ курса. Не следует применять формулы, которые не входят в программу. Решение должно быть доведено до окончательного ответа.
Требования к выполнению и оформлению контрольной работы
1. Каждая работа выполняется в отдельной тетради школьного формата. Следует пронумеровать страницы и оставить на них поля не менее 3 см для замечаний преподавателя.
2. На обложке тетради должен быть приклеен титульный лист утвержденного образца или аккуратно записаны все данные титульного листа; шифр, специальность, если она не отражена в шифре, фамилия, имя, отчество учащегося, предмет и номер работы.
3. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво.
4. Каждую задачу надо начинать с новой страницы.
5. Решение задач желательно располагать в порядке номеров, указанных в задании, номера задач следует указывать перед условием.
6. Условия задач должны быть обязательно переписаны полностью в контрольную тетрадь; к геометрическим задачам, кроме того, дается установленная краткая запись условия.
7. При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения. Перечислим важнейшие из этих требований:
а) учащиеся должны соблюдать абзацы, всякую новую мысль следует начинать с красной строки;
б) важные формулы, равенства, определения нужно выделять в отдельные строки, чтобы сделать их более обозримыми;
в) при описании решения задачи краткая запись условия отделяется от решения и в конце решения ставится ответ;
г) серьезное внимание следует уделять правильному написанию сокращенных единиц величин;
д) необходимо правильно употреблять математические символы.
8. Решения задач должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.
9. Чертежи следует выполнять карандашом с использованием чертежных инструментов, соблюдая масштаб.
10. В конце работы следует указать литературу, которой вы пользовались, проставить дату выполнения работы и подпись.
11. Если в работе допущены недочеты и ошибки, то учащийся должен выполнить все указания преподавателя, сделанные в рецензии.
12 Контрольные работы должны быть выполнены в срок (в соответствии с учебным планом-графиком), В период сессии работы на проверку не принимаются.
13. Работа, выполненная не по своему варианту, не учитывается и возвращается учащемуся без оценки.
14. Студенты, не имеющие зачета по контрольной работе, к экзамену не допускаются.
15. Во время экзамена зачтенные контрольные работы представляются преподавателю вместе с данными методическими указаниями.
16. Контрольная работа имеет 50 вариантов. Вариант работы выбирается по двум последним цифрам шифра (номера личного дела). Например, студенты, имеющие шифры 23, 117, 300, 207, получат варианты 23, 17, 00, 07. Студенты, у которых шифры от 1 до 9, должны добавить впереди цифру «0», т. е. они получат варианты 01, 02, 03, ..., 09.
СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ
Введение.
Понятие о предмете «математика». История возникновения, развития и становления математики как основополагающей дисциплины, необходимой для изучения профессиональных дисциплин. Роль математики в современном мире. Цели, задачи математики. Основные понятия и представления. Связь математики с общепрофессиональными и специальными дисциплинами.
В результате изучения темы студент должен
иметь представление:
- о роли математики при изучении общепрофессиональных и специальных дисциплин в профессиональной деятельности.
Тема 1. Комплексные числа.
Определение комплексного числа. Действия над комплексными числами. Тригонометрическая форма комплексного числа. Действия над комплексными числами, заданными в тригонометрической форме. Показательная форма записи комплексного числа. Формула Эйлера.
В результате изучения темы студент должен
иметь представление:
о комплексных числах;
знать:
- определение комплексного числа;
- формы записи комплексного числа;
- правила сложения, умножения, вычитания и деления комплексных чисел;
- формулу Эйлера;
уметь:
- находить сумму, разность, произведение и частное комплексных чисел;
- применять формулу Эйлера.
Тема 2. Пределы.
Определение предела функции. Понятие предела функции в точке и в бесконечности. Основные теоремы о пределах.
В результате изучения темы студент должен
иметь представление:
о пределе функции;
знать:
- определение предела;
-определение бесконечно малой и бесконечно большой функций;
-основные теоремы о пределах;
уметь:
-вычислять пределы функций в точке и в бесконечности, применяя основные теоремы о пределах и правила вычисления.
Комплексные числа.
По данной теме ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки.
Пределы.
Определение1:Число А называется пределом функции f(х) при х →а, если для любого число ε > 0 можно указать δ >0, что для любого х ≠ а, удовлетворяющему неравенству 0<|х – а |<δ, выполняется неравенство |f(х) – А |<ε. В этом случае пишут 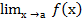 = А.
= А. 
Определение 2:Функция f(х) называется бесконечно малой при х →а, если 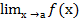 = 0
= 0
Пример1: 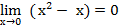
Определение 3: Функция f(х) называется бесконечно большой при х →а, если 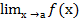 = ± ∞.
= ± ∞.
Пример2: 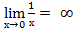 .
.
Свойства бесконечно малой и бесконечно большой функций:
1.Если f(х) – бесконечно малая функция, то 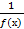 - бесконечно большая функция.
- бесконечно большая функция.
2.Если f(х) – бесконечно большая функция, то 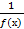 - бесконечно малая функция.
- бесконечно малая функция.
Теоремы о пределах.
Теорема 1:Если существуют пределы функций f(х) и g(х), то существует и предел их суммы, равный сумме пределов функций f(х) и g(х):
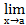 (f(х) + g(х))=
(f(х) + g(х))= 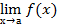 +
+ 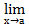 g(x).
g(x).
Теорема 2:Если существуют пределы функций f(х) и g(х), то существует и предел их произведения, равный произведению пределов функций f(х) и g(х):
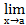 (f(х) * g(х))=
(f(х) * g(х))= 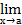 f(x)*.
f(x)*. 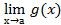
Теорема № 3:Если существуют пределы функций f(х) и g(х), предел функции g(х) отличный от 0, то существует и предел их отношения, равный отношению пределов функций f(х) и g(х):
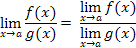
Следствия.
Следствие 1:Постоянный множитель можно выносить за знак предела.
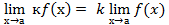
Следствие 2:Предел степени равен степени пределов.
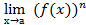 = (
= ( 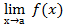 )n.
)n.
Следствие 3: 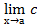 = с.
= с.
Замечательные пределы.
I замечательный предел: 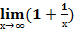 х = е;
х = е; 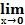
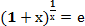 , е = 2,7182818…
, е = 2,7182818…
Пример 13: 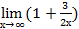 5х =
5х = 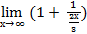 2х/3*3/2*5 =
2х/3*3/2*5 = 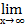 ((1 +
((1 + 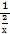 )(3х/3))15/2 =
)(3х/3))15/2 =
( Заменим 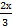 = у и учтём, что у→∞ при х→∞) =
= у и учтём, что у→∞ при х→∞) = 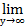 ((1 +
((1 +  )у)15/2 = е15/2
)у)15/2 = е15/2
II замечательный предел: : 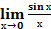 =1;
=1; 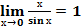 ;
; 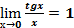
Пример 14: 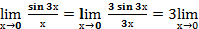
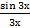 = (заменим 3х = у и учтём, что у→0 при х→0) = 3
= (заменим 3х = у и учтём, что у→0 при х→0) = 3 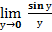 =3*1 = 3
=3*1 = 3
Пример 15: 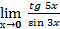 = ( применим формулу
= ( применим формулу 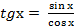 ) =
) = 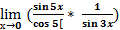 =
= 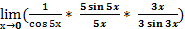 =
= 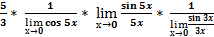 =
= 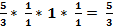
У п р а ж н е н и я д л я с а м о п р о в е р к и:
Вычислите:
1. 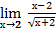 6.
6. 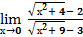
2. 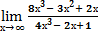 7.
7. 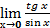
3. 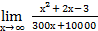 8.
8. 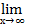
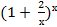
4. 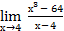 9.
9. 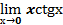
5. 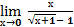 10.
10. 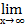
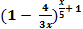
Ответы:1. 0; 2.2; 3.∞; 4.48; 5. 32; 6.1,5; 7.1; 8. 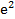 ; 9.1; 10.
; 9.1; 10. 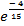 .
.
Дифференциальное исчисление
По данной теме ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Выполните упражнения для самопроверки.
Производная и ее приложения
Производная. Понятие производной является одним из фундаментальных понятий к математике. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.
Пусть функция 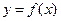 определена в промежутке
определена в промежутке 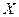 . Возьмем из этого промежутка фиксированное значение аргумента x и придадим ему приращение
. Возьмем из этого промежутка фиксированное значение аргумента x и придадим ему приращение 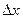 так, чтобы новое значение аргумента
так, чтобы новое значение аргумента 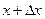 принадлежало этому промежутку. Тогда значение функции
принадлежало этому промежутку. Тогда значение функции 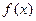 заменится новым значением
заменится новым значением 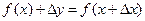 , т.е. функция получит приращение
, т.е. функция получит приращение 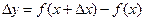 .
.
Определение 1.Предел отношения приращения функции 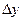 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента 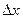 при стремлении
при стремлении 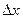 к нулю, т.е.
к нулю, т.е.
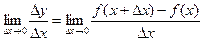 ,
,
называется производной функции 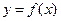 по аргументу x в точке x.
по аргументу x в точке x.
Производная обозначается одним из символов: 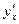 ,
, 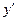 ,
, 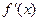 , а ее значение при
, а ее значение при 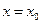 обозначается
обозначается 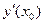 ,
, 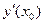 ,
, 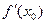 .
.
Определение 2.Операция нахождения производной называется дифференцированием.
Если функция 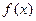 имеет производную в точке x, то она называется дифференцируемой в этой точке.
имеет производную в точке x, то она называется дифференцируемой в этой точке.
Если функция 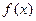 имеет производную в каждой точке промежутка X, то говорят, что эта функция дифференцируема на этом промежутке.
имеет производную в каждой точке промежутка X, то говорят, что эта функция дифференцируема на этом промежутке.
Производная сложной функции.
Определение 3. Пусть 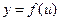 , где u является не независимой переменной, а функцией независимой переменной x:
, где u является не независимой переменной, а функцией независимой переменной x: 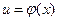 . Таким образом,
. Таким образом, 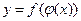 .
.
В этом случае функция y называется сложной функцией x, а переменная u – промежуточным аргументом.
Производная сложной функции находится на основании следующей теоремы: если 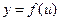 и
и 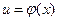 - дифференцируемые функции своих аргументов, то производная сложной функции
- дифференцируемые функции своих аргументов, то производная сложной функции 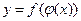 существует и равна произведению производной функции y по промежуточному аргументу и на производной промежуточного аргумента и по независимой переменной x:
существует и равна произведению производной функции y по промежуточному аргументу и на производной промежуточного аргумента и по независимой переменной x:
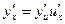 .
.
Эта теорема распространяется и на сложные функции, которые задаются с помощью цепочки, содержащей три звена и более.
Например, если 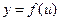 ,
, 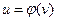 ,
, 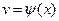 , т.е.
, т.е. 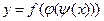 , то
, то 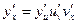 .
.
Формулы дифференцирования. Во всех приведенных ниже формулах буквами u и v обозначены дифференцируемые функции независимой переменной x: 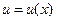 ,
, 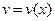 , а буквами a, c, n – постоянные:
, а буквами a, c, n – постоянные:
1. 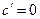
2. 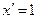
3. 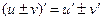
4. 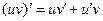
5. 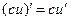
6. 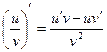
Остальные формулы записаны как для функций независимой переменной, так и для сложных функций:
7. 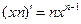
8. 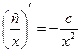
9. 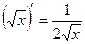
10. 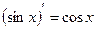
11. 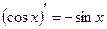
12. 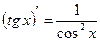
13. 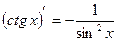
14. 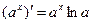
15. 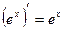
16. 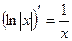
17. 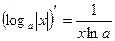
7а. 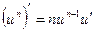
8а. 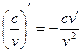
9а. 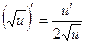
10а. 
11а. 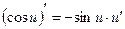
12а. 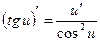
13а. 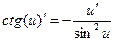
14а. 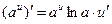
15а. 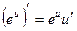
16а. 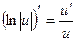
17а. 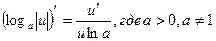
При решении приведенных ниже примеров сделаны подробные записи. Однако следует научиться дифференцировать без промежуточных записей.
Пример 1. Найти производную функции 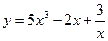 .
.
Решение. Данная функция есть алгебраическая сумма функций. Дифференцируем ее, используя формулы 3, 5, 7 и 8:
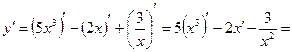
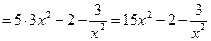
Пример 2. Найти производную функции 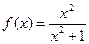
Решение. Применяя формулы 6, 3, 7 и 1, получим
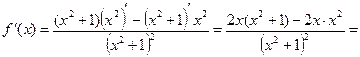
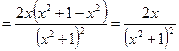
Пример 3. Найти производную функции 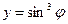 и вычислить ее значение при
и вычислить ее значение при 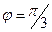
Решение. Это сложная функция с промежуточным аргументом 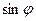 . Используя формулы 7а и 10, имеем
. Используя формулы 7а и 10, имеем
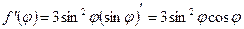 .
.
Вычислим значение производной при 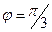 :
:
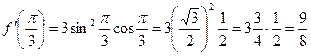 .
.
Пример 4. Найти производную функции 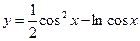 .
.
Решение. Это сложная функция с промежуточным аргументом 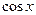 . Применяя формулы 3, 5, 7а, 11, 16а, получим
. Применяя формулы 3, 5, 7а, 11, 16а, получим
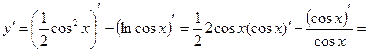
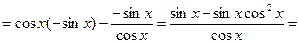
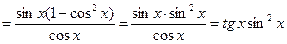
Пример 5. Найти производную функции 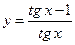 .
.
Решение. Дифференцируем данную функцию по формулам 6, 12, 3 и 1:
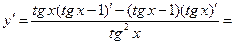
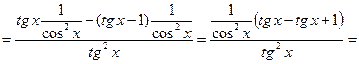
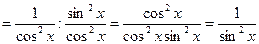
Пример 6. Найти производную функции 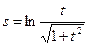 и вычислить ее значение при
и вычислить ее значение при 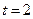 .
.
Решение. Сначала преобразуем функцию, используя свойства логарифмов:
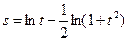
Теперь дифференцируем по формулам 3, 16а, 7 и 1:
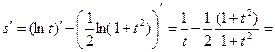
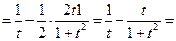
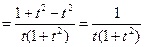 .
.
Вычислим значение производной при 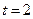 .
.
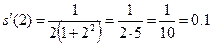
Пример 7. Найти производную функции 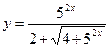 и вычислить ее значение при
и вычислить ее значение при 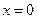 .
.
Решение. Используем формулы 6, 3, 14а, 9а, 5 и 1:
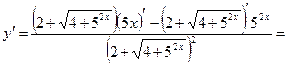
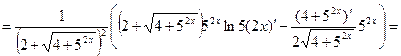
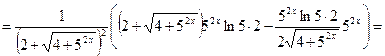
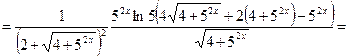
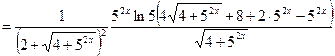
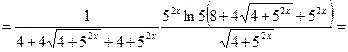
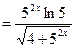 .
.
Вычислим значение производной при 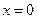 :
:
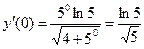 .
.
Геометрический смысл производной.Производная функции имеет простую и важную геометрическую интерпретацию.
Если функция 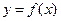 дифференцируема в точке х, то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен значению производной в рассматриваемой точке.
дифференцируема в точке х, то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен значению производной в рассматриваемой точке.
Угловой коэффициент касательной, проведенной к графику функции 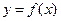 в точке (х0, у0), равен значению производной функции при х=х0, т.е.
в точке (х0, у0), равен значению производной функции при х=х0, т.е. 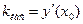 .
.
Уравнение этой касательной имеет вид
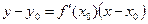 .
.
Пример 8. Составить уравнение касательной к графику функции 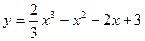 в точке А (3,6).
в точке А (3,6).
Решение. Для нахождения углового коэффициента касательной найдем производную данной функции:
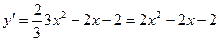 .
.
Угловой коэффициент касательной равен значению производной функции при х=3:
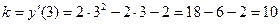 .
.
Уравнение касательной имеет вид
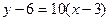 , или
, или 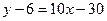 , т.е.
, т.е. 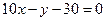
Пример 9. Составить уравнение касательной, проведенной к графику функции 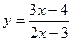 в точке с абсциссой х=2.
в точке с абсциссой х=2.
Решение. Сначала найдем ординату точки касания 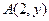 . Так как точка А лежит на кривой, то ее координаты удовлетворяют уравнению кривой, т.е.
. Так как точка А лежит на кривой, то ее координаты удовлетворяют уравнению кривой, т.е.
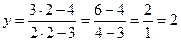 ;
; 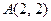 .
.
Уравнение касательной, проведенной к кривой в точке 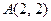 , имеет вид
, имеет вид 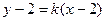 . Для нахождения углового коэффициента касательной найдем производную:
. Для нахождения углового коэффициента касательной найдем производную:
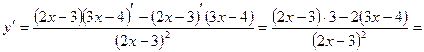
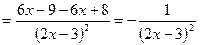 .
.
Угловой коэффициент касательной равен значению производной функции при х=2:
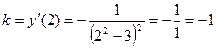
Уравнение касательной таково:
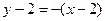 ,
, 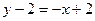 , т.е.
, т.е. 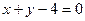
Физический смысл производной. Если тело движется по прямой по закону s=s(t), то за промежуток времени 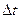 (от момента t до момента
(от момента t до момента 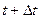 ) оно пройдет некоторый путь
) оно пройдет некоторый путь 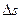 . Тогда
. Тогда 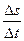 есть средняя скорость движения за промежуток времени
есть средняя скорость движения за промежуток времени 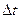 .
.
Скоростью движения тела в данный момент времени t называется предел отношения пути 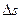 к приращению времени
к приращению времени 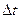 , когда приращение времени стремиться к нулю:
, когда приращение времени стремиться к нулю:
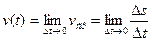 .
.
Следовательно, производная пути s по времени t равна скорости прямолинейного движения тела в данный момент времени:
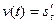 .
.
Скорость протекания физических, химических и других процессов также выражается с помощью производной.
Производная функции 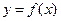 равна скорости изменения этой функции при данном значении аргумента х:
равна скорости изменения этой функции при данном значении аргумента х:
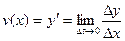
Пример 10.Закон движения точки по прямой задан формулой 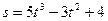 (s – в метрах, t – в секундах). Найти скорость движения точки в конце первой секунды.
(s – в метрах, t – в секундах). Найти скорость движения точки в конце первой секунды.
Решение. Скорость движения точки в данный момент времени равна производной пути s по времени t:
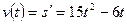 ,
, 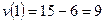
Итак, скорость движения точки в конце первой секунды равна 9 м/с.
Пример 11. Тело, брошенное вертикально вверх, движется по закону 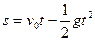 , где v0 – начальная скорость, g –ускорение свободного падения тела. Найти скорость этого движения для любого момента времени t. Сколько времени будет подниматься тело и на какую высоту оно поднимется, если v0=40 м/с?
, где v0 – начальная скорость, g –ускорение свободного падения тела. Найти скорость этого движения для любого момента времени t. Сколько времени будет подниматься тело и на какую высоту оно поднимется, если v0=40 м/с?
Решение. Скорость движения точки в данный момент времени t равна производной пути s по времени t:
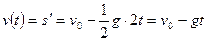 .
.
В высшей точке подъема скорость тела равна нулю:
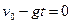 ,
, 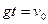 ,
, 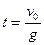 ,
, 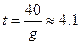 ,
, 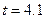 с.
с.
За 40/g секунд тело поднимается на высоту
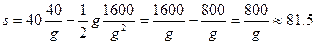 ,
, 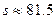 м.
м.
Вторая производная. Производная функции 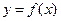 в общем случае является функцией от х. Если от этой функции вычислить производную, то получим производную второго порядка или вторую производную функции
в общем случае является функцией от х. Если от этой функции вычислить производную, то получим производную второго порядка или вторую производную функции 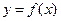 .
.
Определение 4. Второй производной функции 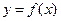 называется производная от ее первой производной
называется производная от ее первой производной 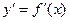 .
.
Вторая производная функции обозначается одним из символов – 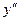 ,
, 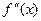 ,
, 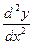 . Таким образом,
. Таким образом, 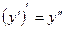 .
.
Аналогично определяются и обозначаются производные любого порядка. Например, производная третьего порядка:
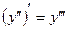 или
или 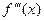 ,
, 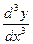
Пример 12.Найти вторую производную функции 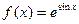 .
.
Решение. Сначала найдем первую производную
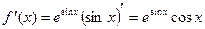
Дифференцируя еще раз, найдем вторую производную:
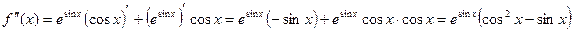 .
.
Пример 13. Найти вторую производную функции 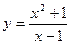 и вычислить ее значение при х=2.
и вычислить ее значение при х=2.
Решение. Сначала найдем первую производную:
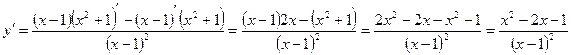
Дифференцируя еще раз, найдем вторую производную:
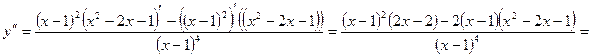
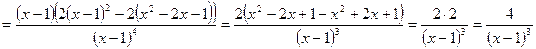 .
.
Вычислим значение второй производной при х=2; имеем 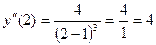
Физический смысл второй производной.Если тело движется прямолинейно по закону s=s(t), то вторая производная пути s по времени t равна ускорению движения тела в данный момент времени t:
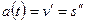
Таким образом, первая производная характеризует скорость некоторого процесса, а вторая производная – ускорение того же процесса.
Пример 14. Точка движется по прямой по закону 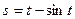 . Найти скорость и ускорение движения
. Найти скорость и ускорение движения 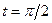 .
.
Решение. Скорость движения тела в данный момент времени равна производной пути s по времени t, а ускорение – второй производной пути s по времени t. Находим:
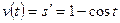 ; тогда
; тогда 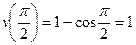 ;
;
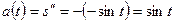 ; тогда
; тогда 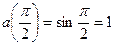
Пример 15.Скорость прямолинейного движения пропорциональна квадратному корню из пройденного пути (как, например, при свободном падении). Доказать, что это движение происходит под действием постоянной силы.
Решение. По закону Ньютона, сила F, вызывающая движение, пропорциональна ускорению, т.е.
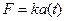 или
или 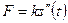
Согласно условию, 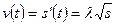 . Дифференцируя это равенство, найдем
. Дифференцируя это равенство, найдем
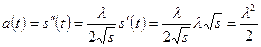
Следовательно, действующая сила 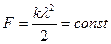 .
.
Приложения производной к исследованию функции.
Приложения производной к исследованию функции.
1)Условие возрастания функции: Дифференцируемая функция y = f(x) монотонно возрастает на промежутке Х тогда и только тогда, когда её производная больше ноля, т. е. y = f(x)↑ f’(x)>0. Это условие геометрически означает, чтокасательная к графику данной функции образует острый угол с положительным направлением к оси оХ.

 У
У
 y = f(x)
y = f(x)
 0 α
0 α
Х
2)Условие убывания функции: Дифференцируемая функция y = f(x) монотонно убывает на промежутке Х тогда и только тогда, когда её производная меньше ноля, т. е.
y = f(x)↓  f’(x)<0 .Это условие геометрически означает, чтокасательная к графику данной функции образует тупой угол с положительным направлением оси оХ)
f’(x)<0 .Это условие геометрически означает, чтокасательная к графику данной функции образует тупой угол с положительным направлением оси оХ)
 У
У
