Решение систем линейных уравнений по формулам Крамера и методом Гаусса.

1. Решить систему линейных уравнений двумя способами: по формулам Крамера и методом Гаусса .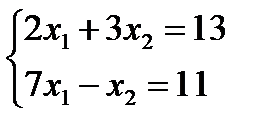

2. Решить систему линейных уравнений с тремя неизвестными двумя способами: по формулам Крамера и методом Гаусса .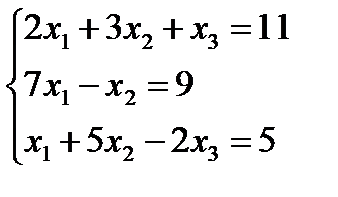

3. Найти общее решение системы линейных алгебраических уравнений и записать одно частное решение этой системы

.

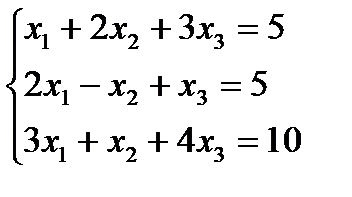Тема 3. Функция. Последовательность

Содержание программы

3.1. Понятие функции, ее свойства, график. Сложная функция. Обратная функция.

3.2. Элементарные функции. Графики основных элементарных функций. Преобразования графиков.

3.3. Графический метод решения уравнений и систем двух уравнений с двумя неизвестными.

3.4. числовая последовательность. Виды последовательностей.

Содержание темы

Пусть X и Y некоторые числовые множества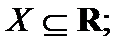

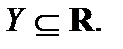
Если каждому 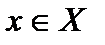по некоторому правилу f ставится в соответствие единственный элемент 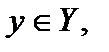то говорят, что задана функция. Обозначается 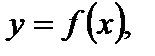где х – аргумент или независимая переменная функции; у – значение функции или зависимая переменная.

Множество Х значений независимой переменной называется областью определения функции и обозначается 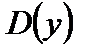или

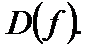
Множество всех значений зависимой переменной Y называется множеством значений функции и обозначается 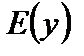или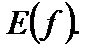

Частное значение функции 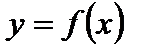при заданном частном значении аргумента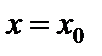 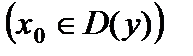обозначается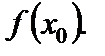

Графиком функции 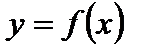называется множество всех точек плоскости с координатами 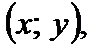где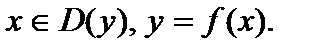

Свойства функции:

1. Четность и нечетность функции.

Функция 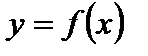называется четной, если:

1) 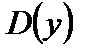– симметричное множество относительно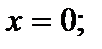

2) для любого 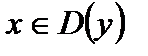выполняется равенство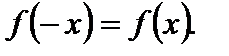

Функция 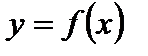называется нечетной, если:

1) 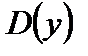– симметричное множество относительно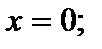

2) для любого 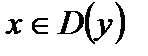выполняется равенство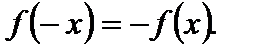

Если функция 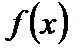является четной или нечетной, то говорят, что она обладает свойством четности.

График четной функции симметричен относительно оси 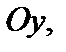график нечетной – относительно начала координат.

2. Периодичность функции.

Функция 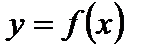с областью определения 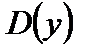называется периодической, если существует такое число 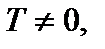что для любого значения 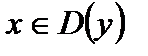выполняются условия:

1)

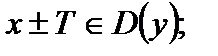
2)

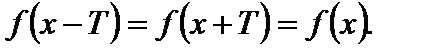
Число Т называется периодом функции.

3. Монотонность функции.

Пусть х₁, х₂ – произвольные значения из области 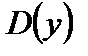функции 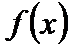такие, что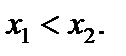

Если при данном условии выполняется:

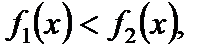то функция называется возрастающей;

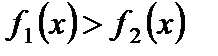– убывающей;

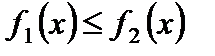– неубывающей;

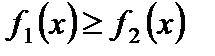– невозрастающей.

4. Промежутки знакопостоянства функции. Нули функции.

Числовые промежутки, на которых функция сохраняет свой знак (т. е. 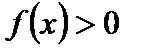или 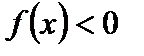), называются промежутками знакопостоянства.

Значения аргумента 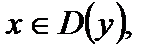при которых функция 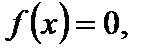называются нулями функции. Нули функции – это точки пересечения графика функции с осью Ох.

Пример 3.1.Найти область определения функции

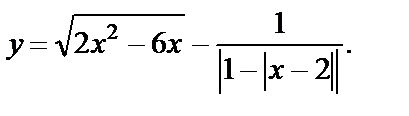
Решение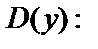

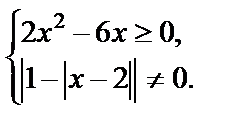(3.1)

Найдем соответствующее 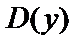множество точек.

Неравенство 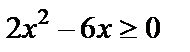равносильно неравенству

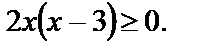
Решая его, получаем: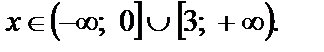

х

–

+

+

Условие 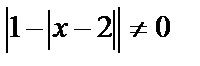означает, что 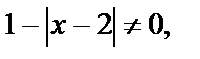т. е.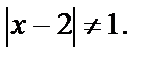

Приходим к заключению, что 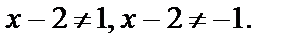Получаем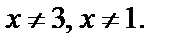

Таким образом, система (3.1) равносильна системе

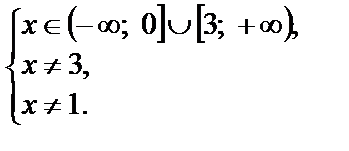
Следовательно,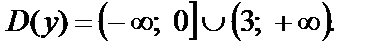

Пример 3.2.Найти множество значений функции

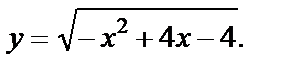
РешениеНайдем область определения функции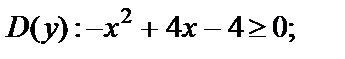

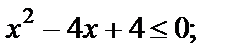
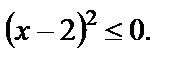
Последнее условие выполняется только для 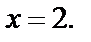Вычисляем значение функции в этой точке: 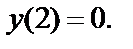Следовательно,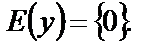

Пример 3.3.Исследовать функцию на четность: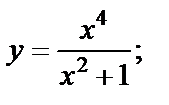

РешениеЗамечаем, что функция 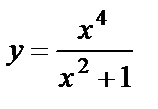имеет 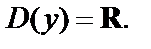Следовательно, функция определена на симметричном множестве.

Рассмотрим ее значение для –х: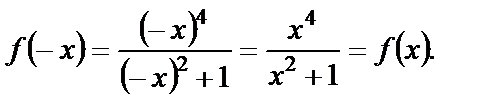

Поскольку выполняются оба условия четности функции, заключаем, что функция 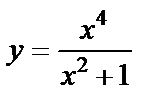– четная.

Преобразования графиков

Приведем графики некоторых функций:

1) 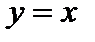– прямая линия; 2) 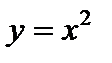– квадратичная парабола;

y = x

y

х

y

х

3) 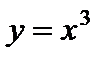– кубическая парабола; 4) 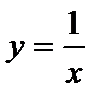– гипербола;

y

x

y = x3

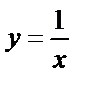y

x

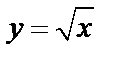y

x

5) 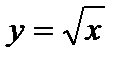– график квадратного корня;

Правила преобразования графиков:

Пусть дана функция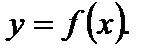

1. Для построения графика функции 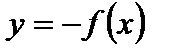исходный график функции 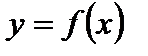симметрично отображаем относительно оси Ох (рис. 1).

2. Для функции 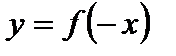заданный график симметрично отображаем относительно оси Оу (рис. 2).

y

x

y = f(x)

y = –f(x)

y

x

y = f(x)

y = f(–x)

Рис. 1 Рис. 2

3. Для функции 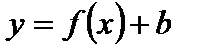этот график получается параллельным переносом графика функции 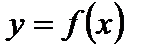на 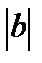масштабных единиц вдоль оси Оу вверх, если 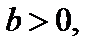и вниз, если 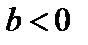(рис. 3).

4. Для функции 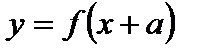этот график получается параллельным переносом графика функции 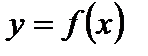на 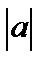масштабных единиц вдоль оси Ох вправо, если 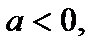и влево, если 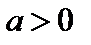(рис. 4).

y

x

y = f(x) + b, b > 0

y = f(x)

y = f(x) + b, b < 0

y = f(x)

y

x

y = f(x + a), a > 0

y = f(x + a), a < 0

Рис. 3 Рис. 4

5. Для функции 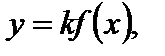где 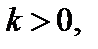график функции 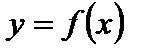«растянут» в k раз вдоль оси Оу (от оси Ох), если 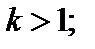«сжат» в 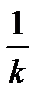раз вдоль оси Оу (к оси Ох), если 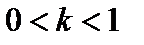(рис. 5).

y = f(x)

y = bf(x), 0 < b < 1

y = bf(x), b > 1

y

х

Рис. 5

6. Для функции 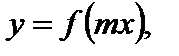где 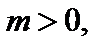график 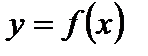«растянут» вдоль оси Ох (от оси Оу) в 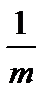раз при 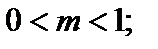«сжат» вдоль Ох (коси Оу) в m раз, при 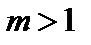(рис. 6).

y = f(ax), 0 <a <1

y = f(ax), a > 1

y = f(x)

y

x

Рис. 6

7. Для функции 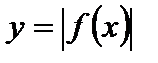сохраняется та часть графика функции 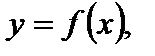которая находится над осью Ох и на оси Ох, а та часть, которая находится под осью Ох, отображается симметрично оси Ох в верхнюю полуплоскость (рис. 7).

y = |f(x)|

y = f(x)

y

x

Рис. 7

8. Для функции 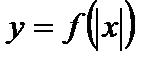часть графика функции 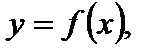соответствующая отрицательному значению х, отбрасывается, а неотрицательному – сохраняется и дополняется симметричной ей относительно оси Оу частью (рис. 8).

y = f(x)

y

x

y = f(|x|)

Рис. 8

Пример 3.4. Построить график функции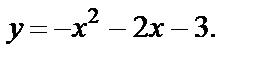

Решение Преобразуем заданную функцию:

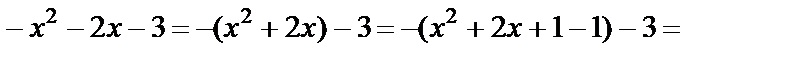
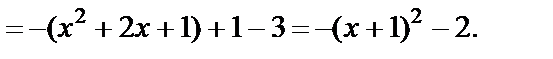
Получили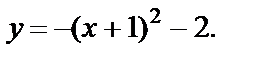

Для построения графика полученной функции используем следующие преобразования:

1) строим график функции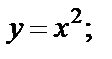

2) график функции 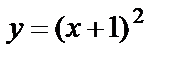получаем из графика функции 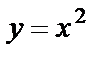путем движения его на единицу влево по оси Ох;

3) график функции 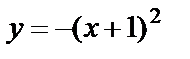получаем из предыдущего симметричным отображением относительно оси Ох;

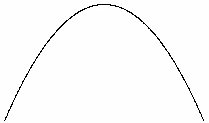
4) график заданной функции получаем из графика функции 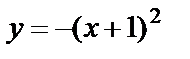параллельным переносом на две единицы вниз по оси Оу (рис. 9).

–3

х

–1

–2

у

1)

2)

3)

4)

Рис. 9

Числовая последовательность

Числовой последовательностью называется функция, определенная на множестве натуральных чисел, которая каждому натуральному числу n ставит в соответствие число 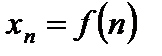. Числовую последовательность обозначают 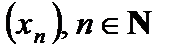, т. е.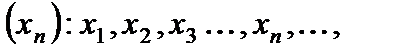

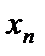– n-й член последовательности, а формула 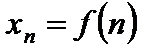называется формулой общего члена последовательности.

Зная функцию 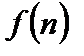и номер n, можно вычислить любой член последовательности.

Пример 3.5. Определить, является ли число 28 членом последовательност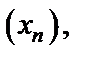и если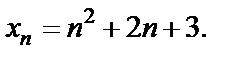

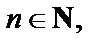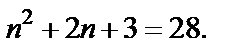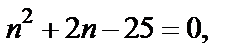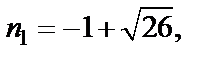
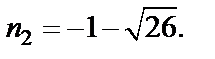Решение Число 28 является членом последовательности, если найдется такой номер для которого выполняется равенство Решим это квадратное уравнение т. е. Числа 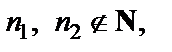следовательно, число 28 не является членом данной последовательности.

Пример 3.6. Вычислить первые пять членов последовательности 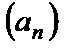, если 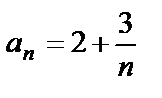. Определить, для каких членов последовательности 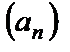выполняется условие .

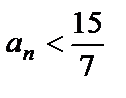Решение Подставляя в формулу общего члена значение n = 1, 2, 3, 4, 5, получим:

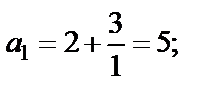
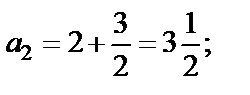
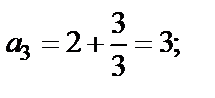
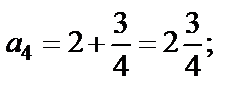
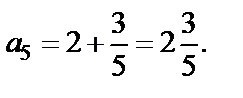
Решим неравенство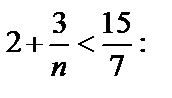

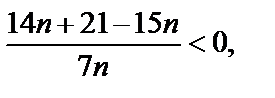
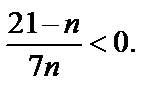
Решением этого неравенства будут 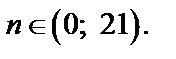Поэтому, для любых членов последовательности с номерами от 1 до 20 включительно выполняется условие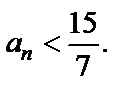

Контрольные врпросы

1. Как определяется функция?

2. Что такое график функции?

3. Какие способы задания функции вы знаете?

4. Какая функция называется четной?

5. Что такое период функции?

6. Что такое промежутки знакопостоянства?

7. Как определяется числовая последовательность?

8. Какими способами можно задать последовательность?

9. Какие последовательности называются монотонными?

10. Что такое ограниченная последовательность?