Тема 3. Интегральное исчисление

Интегрирование как действие и символика интегрального исчисления. Неопределенный интеграл и его свойства. Методы интегрирования (непосредственное интегрирование, введение новой переменной, интегрирование по частям). Табличные интегралы. Понятие определенного интеграла: его свойства и методы вычисления (методы треугольников, трапеций, параболы).

Вычисление геометрических, механических и физических величин с помощью интегрального исчисления. Определение дифференциальных уравнений. Самые распространенные дифференциальные уравнения и их решения (уравнения с разделяющимися переменными, однородные уравнения первого и второго порядка). Неопределенный и определенный интегралы и их свойства. Решение прикладных задач с помощью определенного интеграла.

В результате изучения темы студент должен

иметь представление:

- о табличных интегралах;

- о вычислении геометрических, механических и физических величин с помощью интегрального исчисления;

знать:

- символику и определение интегрального исчисления;

- свойства определенного и неопределенного интегралов;

- методы интегрирования (непосредственного интегрирования, интегрирования по частям, введения новой переменной);

- геометрический смысл определенного интеграла;

- приближенные методы исчисления определенных интегралов (метод прямоугольников, способ трапеции и параболы);

- определение обыкновенного дифференциального уравнения, уравнения с разделяющимися переменными, однородные уравнения 1-го порядка, линейные однородные и неоднородные уравнения высших порядков;

- определение дифференциального уравнения 2-го порядка с постоянными коэффициентами

уметь:

- вычислять неопределенный и определенный интеграл методом замены переменной и по частям, интегрировать рациональные, иррациональные и некоторые тригонометрические функции;

- применять определенные интегралы в геометрии;

- решать обыкновенные дифференциальные уравнения 1-го порядка: с разделяющимися переменными, однородные, в полных дифференциалах, линейные.

- решать дифференциальные уравнения 2-го порядка с постоянными коэффициентами

Тема 4. Теория вероятности и математическая статистика

Понятие события. Определение вероятности. Достоверные и невозможные события. Классическое определение вероятностей. Теорема сложения вероятностей. Теорема умножения вероятностей. Независимость случайных событий. Основные понятия комбинаторики. Математическое ожидание и дисперсия: их свойства, правила вычисления. Функции распределения случайных величин. Задачи математической статистики. Функции выборки. Некоторые важнейшие распределения. Методы оценки параметров распределений. Случайная выборка, понятие генеральной совокупности. Выборочное среднее и выборочные дисперсии. Типовые выборочные распределения.

В результате изучения темы студент должен

иметь представление:

- о случайных событиях;

- об определении вероятности события;

- о задачах математической статистики;

- о случайных выборках;

- о функциях выборки;

- о некоторых важнейших распределениях;

- о методах оценки параметров распределений;

знать:

- понятия: событие, частота и вероятность появления события, совместные и несовместные события, полная вероятность;

- теорему сложения вероятностей;

- теорему умножения вероятностей;

- комбинаторные задачи;

- правила вычисления среднего значения и дисперсии;

- свойства математического ожидания;

- среднее квадратичное отклонение случайной величины;

уметь:

- находить вероятность в простейших задачах, используя классическое определение вероятностей;

- решать задачи с применением теоремы сложения вероятностей для несовместных событий;

- решать задачи раздела «Комбинаторика»;

- вычислять математическое ожидание и дисперсию;

- находить среднее квадратичное отклонение случайной величины.

Методические указания к выполнению контрольной работы № 1

Пределы.

По данной теме ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки.

Определение1:Число А называется пределом функции f(х) при х →а, если для любого число ε > 0 можно указать δ >0, что для любого х ≠ а, удовлетворяющему неравенству 0<|х – а |<δ, выполняется неравенство |f(х) – А |<ε. В этом случае пишут 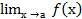= А.

Определение 2:Функция f(х) называется бесконечно малой при х →а, если 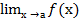= 0

Пример1: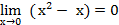

Определение 3: Функция f(х) называется бесконечно большой при х →а, если = ± ∞.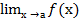

Пример2: .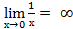

Свойства бесконечно малой и бесконечно большой функций:

1.Если f(х) – бесконечно малая функция, то 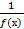- бесконечно большая функция.

2.Если f(х) – бесконечно большая функция, то 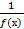- бесконечно малая функция.

Теоремы о пределах.

Теорема 1:Если существуют пределы функций f(х) и g(х), то существует и предел их суммы, равный сумме пределов функций f(х) и g(х):

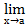(f(х) + g(х))= 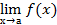+ 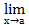g(x).

Теорема 2:Если существуют пределы функций f(х) и g(х), то существует и предел их произведения, равный произведению пределов функций f(х) и g(х):

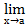(f(х) * g(х))= 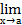f(x)*.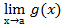

Теорема № 3:Если существуют пределы функций f(х) и g(х), предел функции g(х) отличный от 0, то существует и предел их отношения, равный отношению пределов функций f(х) и g(х): .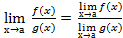

Следствия.

Следствие 1:Постоянный множитель можно выносить за знак предела.

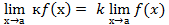
Следствие 2:Предел степени равен степени пределов.

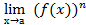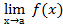= ( )ⁿ.

Следствие 3: 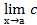= с.