Произведение матрицы на число

Операции над матрицами

Некоторые операции над матрицами, такие как сложение и вычитание, допускаются только для матриц одинакового размера.

Равные матрицы

Определение

Две матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны:

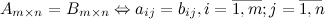
Пример

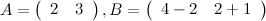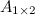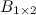. Эти матрицы равны, т.к. равны их размеры: и , а также соответствующие элементы: ;

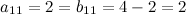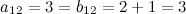
Пример

Задание. Пусть задана матрица 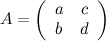. Найти все элементы матрицы , если известно, что она равна матрице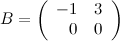

Решение. Так как матрицы и равны, то равны и их соответствующие элементы, т.е.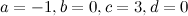

Ответ.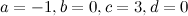

Произведение матрицы на число

Определение

Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число.

Пример

Задание. Пусть 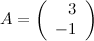. Найти матрицу .

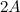Решение.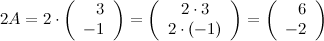

Ответ.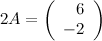

Умножение матрицы на число

Определение

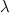Произведением матрицы на ненулевое число называется матрица 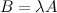того же порядка, полученная из исходной умножением на заданное число всех ее элементов:

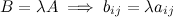
Итак, в результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на заданное число.

Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число, то есть .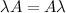

Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

Данная операция, вместе с операцией сложения матриц, относится к линейным операциям над матрицами.

Пример

Задание. Чему равна матрица 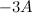, если матрица ?

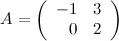Решение.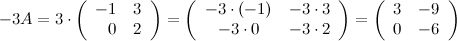

Ответ.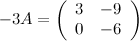

Свойства умножения матрицы на число:

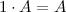
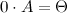
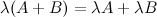
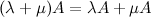
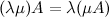
Сумма матриц

Определение

Суммой матриц и одного размера называется матрица 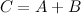такого же размера, получаемая из исходных путем сложения соответствующих элементов.

Пример

Задание. Найти 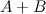, если ,

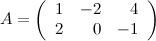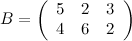
Решение.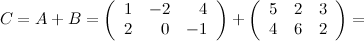

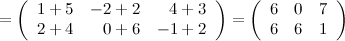
Ответ.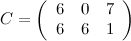

Операции умножение матрицы на число и сумма матриц называются линейными.

Свойства линейных операций:

Везде далее матрицы , и 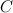- матрицы одного размера.

Ассоциативность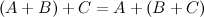

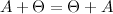, где 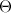- нулевая матрица соответствующего размера.

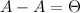
Коммутативность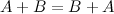

Дистрибутивность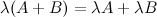

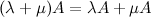
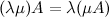
Сложение и вычитание матриц

Сложение и вычитание матриц, допускаются только для матриц одинакового размера.

Сумма матриц

Определение

Суммой матриц и одного размера называется матрица 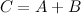такого же размера, получаемая из исходных путем сложения соответствующих элементов:

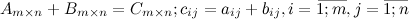
Замечание

Складывать можно только матрицы одинакового размера.

Пример

Задание. Найти 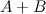, если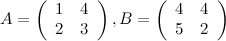

Решение.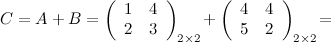

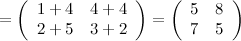
Ответ.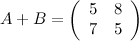

Свойства сложения и вычитания матриц:

Ассоциативность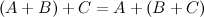

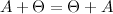, где 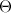- нулевая матрица соответствующего размера.

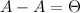
Коммутативность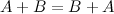

Разность матриц

Разность двух матриц одинакового размера можно определить через операцию сложения матриц и черезумножение матрицы на число.

Вычитание матриц вводится следующим образом: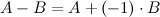

То есть к матрице прибавляется матрица , умноженная на (-1).

Определение

Разностью матриц и одного и того же размера называется матрица 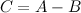такого же размера, получаемая из исходных путем прибавления к матрице матрицы , умноженной на (-1).

На практике же от элементов матрицы попросту отнимают соответствующие элементы матрицы при условии, что заданные матрицы одного размера.

Замечание

Вычитать можно только матрицы одинакового размера.

Пример

Задание. Найти матрицу 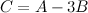, если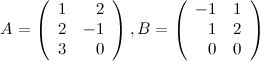

Решение.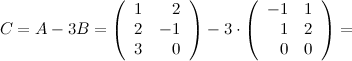

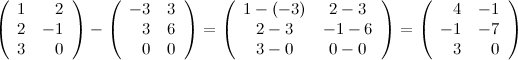
Ответ.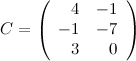

Произведение двух матриц

Определение

Произведением матрицы 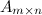на матрицу 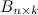называется матрица 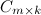такая, что элемент матрицы 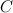, стоящий в 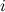-ой строке и 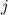-ом столбце, т.е. элемент 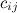, равен сумме произведений элементов 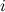-ой строки матрицы на соответствующие элементы 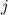-ого столбца матрицы .

Пример

Задание. Найти 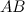, если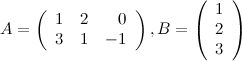

Решение. Так как 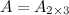, а 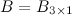, то в результате получим матрицу размера 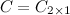, т.е. матрицу вида 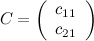. Найдем элементы данной матрицы:

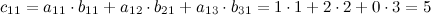
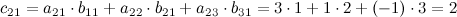
Таким образом, получаем, что:

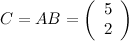
Все вычисления можно было сделать в более компактном виде:

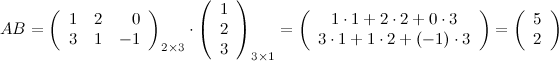
Ответ.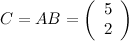

Свойства произведения матриц:

Ассоциативность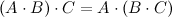

Ассоциативность по умножению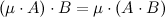

Дистрибутивность ,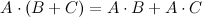

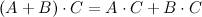
Умножение на единичную матрицу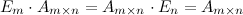

В общем случае умножение матриц не коммутативно, т.е.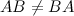

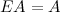
Умножение матриц

Определение

Произведением матрицы 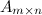на матрицу 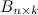называется матрица 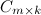такая, что элемент матрицы 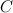, стоящий в 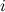-ой строке и 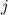-ом столбце, т.е. элемент 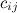, равен сумме произведений элементов 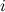-ой строки матрицы на соответствующие элементы 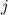-ого столбца матрицы .

Замечание

Умножать матрицы можно тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.

Пример

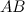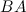Задание. Вычислить и , если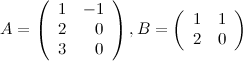

Решение. Так как 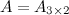, а 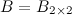, то произведение возможно и результатом операции умножения будет матрица 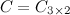, а это матрица вида .

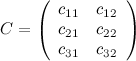Вычислим элементы матрицы :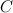

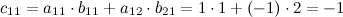
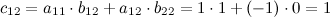
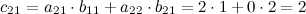
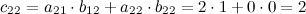
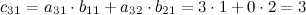
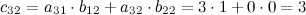
Итак, .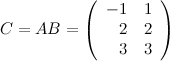

Выполним произведения в более компактном виде:

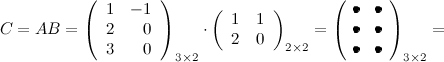
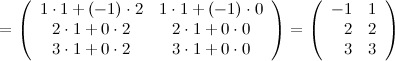
Найдем теперь произведение 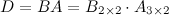. Так как количество столбцов матрицы (первый сомножитель) не совпадает с количеством строк матрицы (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.

Ответ. 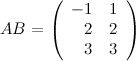. В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы не совпадает с количеством строк матрицы .

Свойства произведения матриц:

1. Ассоциативность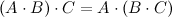

2. Ассоциативность по умножению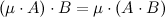

3. Дистрибутивность ,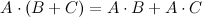

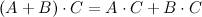
4. Умножение на единичную матрицу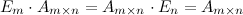

5. В общем случае умножение матриц не коммутативно, т.е.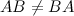

6.

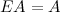
Транспонирование матрицы

Определение

Транспонирование матрицы - это операция над матрицей, когда ее строки становятся столбцами с теми же номерами.

Пример

Задание. Найти матрицу 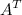, если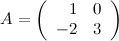

Решение.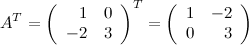

Ответ.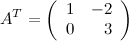

Пример

Задание. Найти транспонированную матрицу 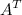, если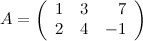

Решение.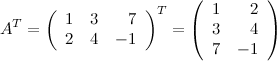

Если матрица - это матрица размера 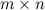, то матрица 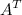имеет размер .

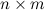Свойства операции транспонирования матриц:

1.

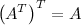
2.

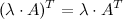
3.

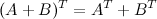
4.

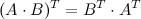
Элементарные преобразования над строками матрицы.
Эквивалентные матрицы

Определение

Элементарными преобразованиями над строками матриц называются следующие преобразования строк:

1. умножение строки на ненулевое число;

2. перестановка двух строк;

3. прибавление к одной строке матрицы другой ее строки, умноженной на некоторое ненулевое число.

Если от матрицы к матрице перешли с помощью эквивалентных преобразований над строками, то такие матрицы называются эквивалентными и обозначают .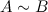

Примеры элементарных преобразований

Продемонстрируем все элементарные преобразования на примере матрицы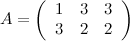

Умножим первую строку матрицы на два, то есть каждый элемент первой строки умножаем на двойку, в результате получим матрицу , эквивалентную заданной матрице :

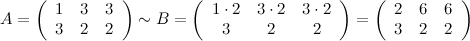
Поменяем первую и вторую строки матрицы местами, получаем эквивалентную ей матрицу :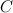

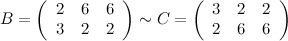
От первой строки матрицы 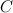отнимем вторую строку, получаем эквивалентную матрицу :

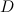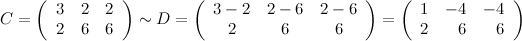
В итоге делаем вывод, что матрицы и 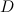эквивалентны, так как от одной из них перешли к другой при помощи эквивалентных преобразований над строками.

Определение

Квадратной матрице 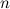-го порядка ставиться в соответствие число , называемое определителем матрицы или детерминантом.

Свойства определителей:

Замечание

Все что будет сказано относительно строк, будет относиться и к столбцам.

1° При транспонировании квадратной матрицы её определитель не меняется: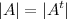

Пример

Известно, что определитель матрицы 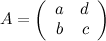равен 3. Тогда определитель матрицы 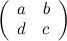, которая равна 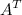, также равен 3.

2° Общий множитель в строке можно выносить за знак определителя.

Пример

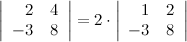
3°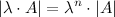

То есть, если квадратная матрица 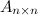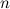-го порядка умножается на некоторое ненулевое число 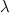, то определитель полученной матрицы равен произведению определителя исходной матрицы на число 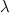в степени, равной порядку матриц.

Пример

Задание. Пусть определитель матрицы третьего порядка равен 3, вычислить определитель матрицы .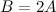

Решение. По свойству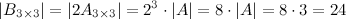

Ответ.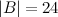

4° Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

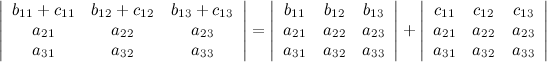
5° Если две строки определителя поменять местами, то определитель поменяет знак.

Пример

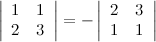
6° Определитель с двумя равными строками равен нулю.

Пример

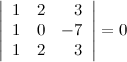
7° Определитель с двумя пропорциональными строками равен нулю.

Пример

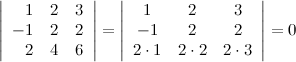
8° Определитель, содержащий нулевую строку, равен нулю.

Пример

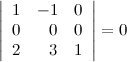
9° Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.

Пример

Пусть задан определитель третьего порядка 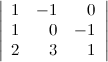. Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:

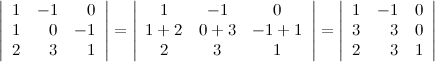
10° Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

Пример

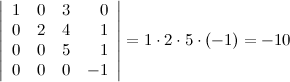
11° Определитель произведения матриц равен произведению определителей: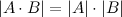

Минор

Определение

Минором 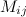к элементу 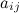определителя 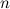-го порядка называется определитель 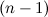-го порядка, полученный из исходного вычеркиванием 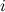-той строки и 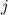-того столбца.

Пример

Задание. Найти минор 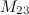к элементу 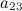определителя .

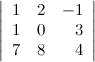Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:

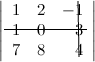
тогда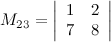

Ответ.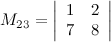

Алгебраическое дополнение

Определение

Алгебраическим дополнением 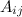к элементу 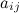определителя 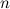-го порядка называется число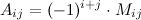

Пример

Задание. Найти алгебраическое дополнение 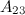к элементу 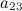определителя .

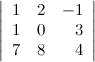Решение.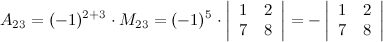

Ответ.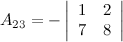

Сумма произведений элементов "произвольной" строки на алгебраические дополнения к элементам 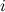-ой строки определителя равна определителю, в котором вместо 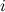-ой строки записана "произвольная" строка.

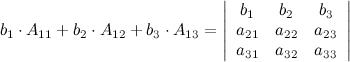
Сумма произведений элементов строки определителя на алгебраические дополнения к элементам другой строки равна нулю.

Правило треугольника

Схематически это правило можно изобразить следующим образом:

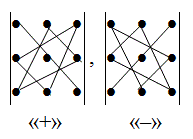
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком "плюс"; аналогично, для второго определителя - соответствующие произведения берутся со знаком "минус", т.е.

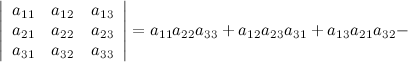
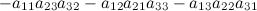
Пример

Задание. Вычислить определитель 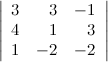методом треугольников.

Решение.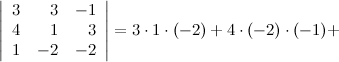

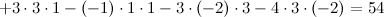
Ответ.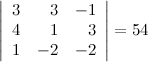

Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":

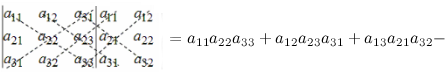
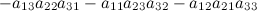
Пример

Задание. Вычислить определитель 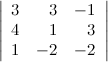с помощью правила Саррюса.

Решение.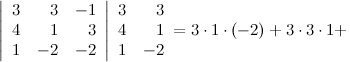

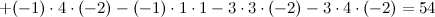
Ответ.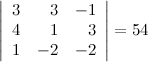

Замечание

Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.

Теорема Лапласа

Теорема

Пусть 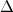- определитель 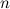-го порядка. Выберем в нем произвольные 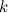строк (или столбцов), причем 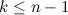. Тогда сумма произведений всех миноров 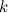-го порядка, которые содержатся в выбранных 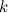строках (столбцах), на их алгебраические дополнения равна определителю.

Пример

Задание. Используя теорему Лапласа, вычислить определитель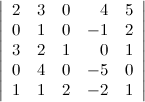

Решение. Выберем в данном определителе пятого порядка две строки - вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):

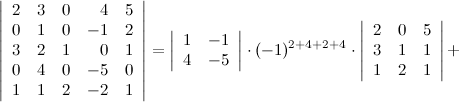
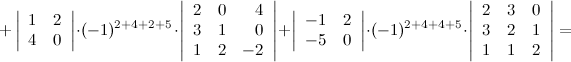
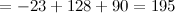
Ответ.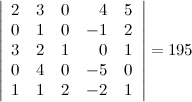

Обратная матрица

На множестве матриц не определена операция деления, она заменена умножением на обратную матрицу.

Определение

Невырожденной называется квадратная матрица, определитель которой не равен нулю. Квадратная матрица называется вырожденной, если ее определитель равен нулю.

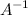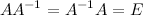Квадратная матрица называется обратной к невырожденной матрице , если , где 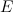- это единичная матрица соответствующего порядка.

Замечание

Обратная матрица существует только для квадратных матриц с не равными нулюопределителями.

Свойства обратной матрицы:

1°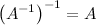

2°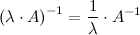

3°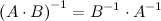

4°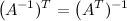

Операции над матрицами

Некоторые операции над матрицами, такие как сложение и вычитание, допускаются только для матриц одинакового размера.

Равные матрицы

Определение

Две матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны:

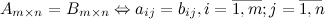
Пример

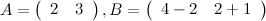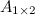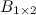. Эти матрицы равны, т.к. равны их размеры: и , а также соответствующие элементы: ;

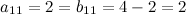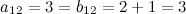
Пример

Задание. Пусть задана матрица 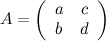. Найти все элементы матрицы , если известно, что она равна матрице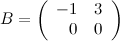

Решение. Так как матрицы и равны, то равны и их соответствующие элементы, т.е.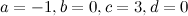

Ответ.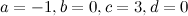

Произведение матрицы на число

Определение

Произведением матрицы на число называется матрица, полученная из исходной умножением каждого ее элемента на заданное число.

Пример

Задание. Пусть 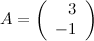. Найти матрицу .

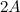Решение.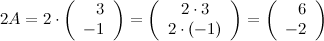

Ответ.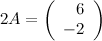

Умножение матрицы на число

Определение

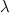Произведением матрицы на ненулевое число называется матрица 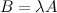того же порядка, полученная из исходной умножением на заданное число всех ее элементов:

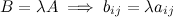
Итак, в результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на заданное число.

Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число, то есть .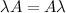

Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

Данная операция, вместе с операцией сложения матриц, относится к линейным операциям над матрицами.

Пример

Задание. Чему равна матрица 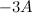, если матрица ?

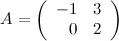Решение.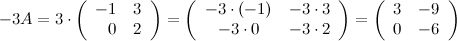

Ответ.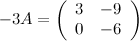

Свойства умножения матрицы на число:

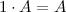
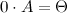
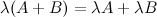
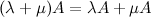
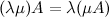
Сумма матриц

Определение

Суммой матриц и одного размера называется матрица 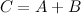такого же размера, получаемая из исходных путем сложения соответствующих элементов.

Пример

Задание. Найти 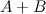, если ,

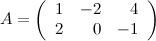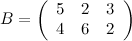
Решение.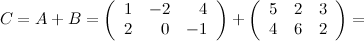

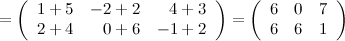
Ответ.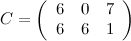

Операции умножение матрицы на число и сумма матриц называются линейными.

Свойства линейных операций:

Везде далее матрицы , и 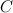- матрицы одного размера.

Ассоциативность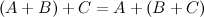

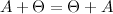, где 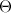- нулевая матрица соответствующего размера.

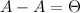
Коммутативность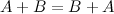

Дистрибутивность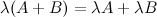

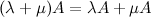
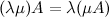
Сложение и вычитание матриц

Сложение и вычитание матриц, допускаются только для матриц одинакового размера.

Сумма матриц

Определение

Суммой матриц и одного размера называется матрица 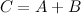такого же размера, получаемая из исходных путем сложения соответствующих элементов:

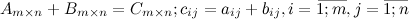
Замечание

Складывать можно только матрицы одинакового размера.

Пример

Задание. Найти 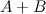, если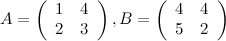

Решение.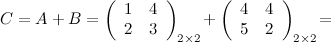

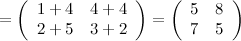
Ответ.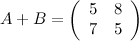

Свойства сложения и вычитания матриц:

Ассоциативность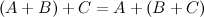

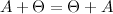, где 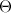- нулевая матрица соответствующего размера.

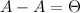
Коммутативность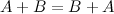

Разность матриц

Разность двух матриц одинакового размера можно определить через операцию сложения матриц и черезумножение матрицы на число.

Вычитание матриц вводится следующим образом: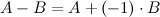

То есть к матрице прибавляется матрица , умноженная на (-1).

Определение

Разностью матриц и одного и того же размера называется матрица 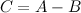такого же размера, получаемая из исходных путем прибавления к матрице матрицы , умноженной на (-1).

На практике же от элементов матрицы попросту отнимают соответствующие элементы матрицы при условии, что заданные матрицы одного размера.

Замечание

Вычитать можно только матрицы одинакового размера.

Пример

Задание. Найти матрицу 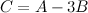, если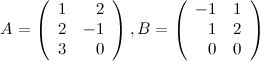

Решение.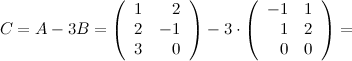

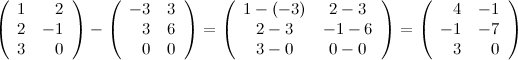
Ответ.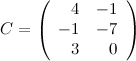

Произведение двух матриц

Определение

Произведением матрицы 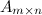на матрицу 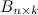называется матрица 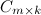такая, что элемент матрицы 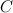, стоящий в 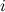-ой строке и 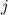-ом столбце, т.е. элемент 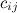, равен сумме произведений элементов 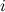-ой строки матрицы на соответствующие элементы 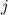-ого столбца матрицы .

Пример

Задание. Найти 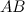, если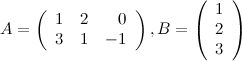

Решение. Так как 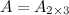, а 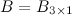, то в результате получим матрицу размера 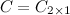, т.е. матрицу вида 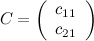. Найдем элементы данной матрицы:

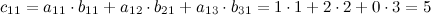
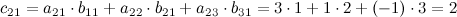
Таким образом, получаем, что:

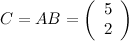
Все вычисления можно было сделать в более компактном виде:

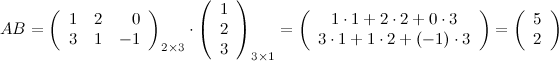
Ответ.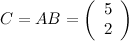

Свойства произведения матриц:

Ассоциативность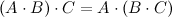

Ассоциативность по умножению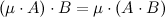

Дистрибутивность ,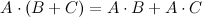

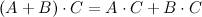
Умножение на единичную матрицу