Применение производной в геометрии

Производная функции 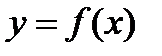в некоторой точ­ке 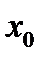численно равна угловому коэффициенту касательной к графику функции в точке .

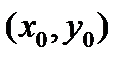Касательной к графику функции 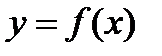, дифференцируемой в точке х₀, называется прямая, проходящая через точку 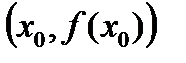и имеющая угловой коэффициент

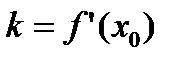.(2.22)

Пример 2.18. Найти уравнение касательной к графику функции 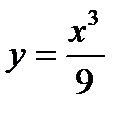в точке с абсциссой 2.

Решение.По условию х₀ = 2. Поэтому 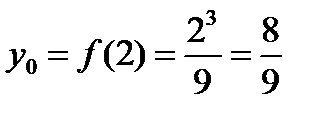. Та­ким образом, нужно построить касательную к графику данной функции в точке 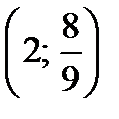. Графиком дан­ной функции является кубическая парабола, проходящая через начало координат и симметричная относительно начала коорди­нат. Найдем угловой коэффициент касатель­ной в точке с абсциссой 2, т. е. значение производной в этой точке:

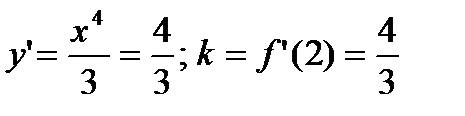Следовательно, касательная – это прямая, проходящая через точку 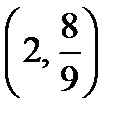и имеющая угловой коэффициент 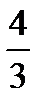, то есть прямая 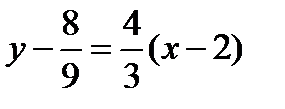. Построим эту прямую по двум точкам с координатами 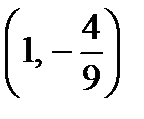и

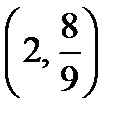
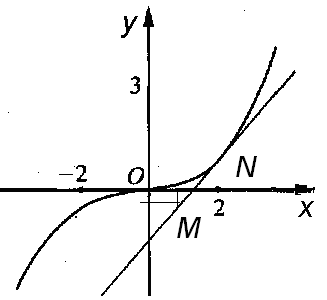
Таким обра­зом, касательная к заданной параболе проходит через две точк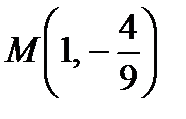и: и 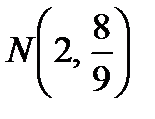, причем в точке N касается графика кубической параболы .

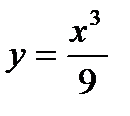Пример 2.19. Найдите угол наклона касательной к параболе 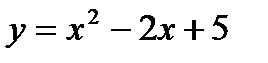в точках .

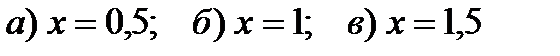Решение.

а)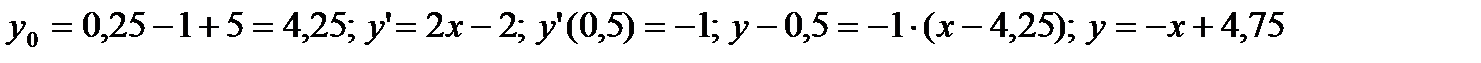

б)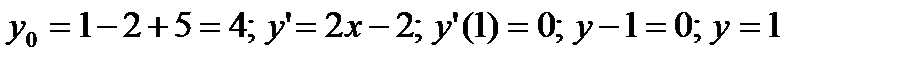

в)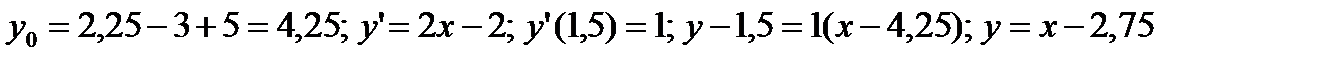

Пример 2.20. Определите углы, под которыми синусоида и тангенсоида пересекают ось абсцисс.

Решение.

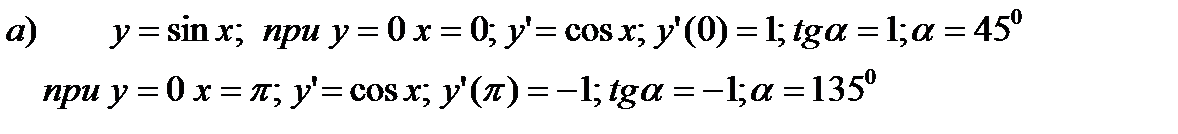
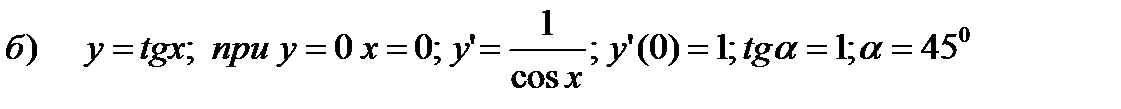
Пример 2.21. Под каким углом синусоида пересекает прямую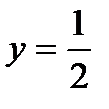

Решение. 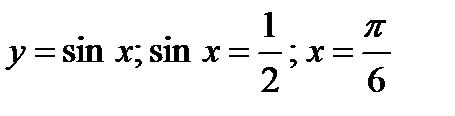- абсцисса точки пересечения синусоиды и прямой.

Координаты точки пересечения .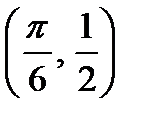

Определим углы наклона касательных с графиком функций в названных точках.

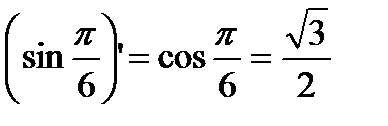- тангенс угла наклона синусоиды к оси x. Поскольку прямая параллельна этой оси, то 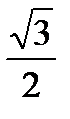является тангенсом угла между этой прямой и синусоидой. Таким образом, .

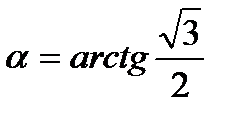Пример 2.22. Докажите, что гиперболы 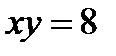и 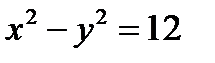пересекаются под прямым углом.

Решение.

1) Определим координаты точки пересечения гипербол.

Из первого уравнения: 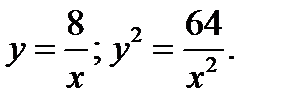Из второго уравнения 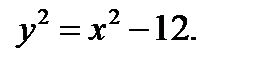Таким образом, получим: .

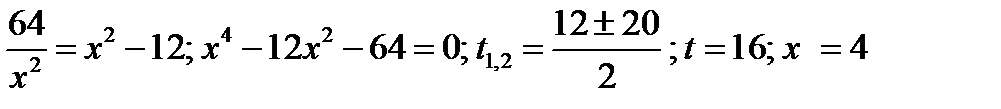Таким образом, ордината точки пересечения гипербол равна 2. Определим углы наклона к оси x касательных к каждой из гипербол в указанной точке.

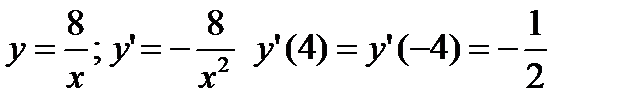- первая гипербола .

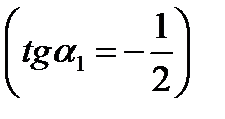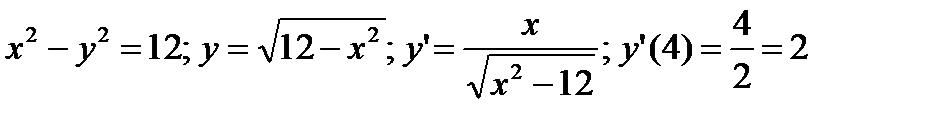- вторая гипербола .

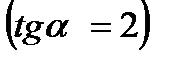Получили: 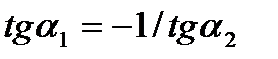, что является признаком перпендикулярности касательных, а, значит, и гипербол.

Пример 2.23. Определите угол, под которым пересекаются лини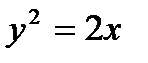и

и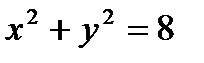

Решение.

1) Ордината точки пересечения: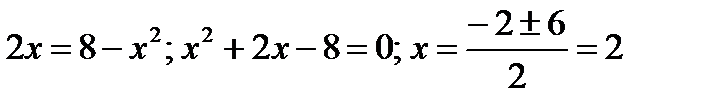

2) Углы наклона касательных к оси x:

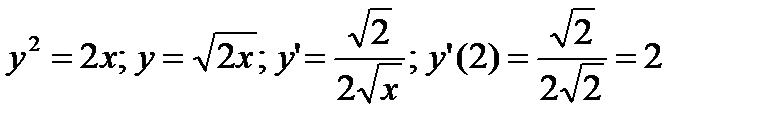- для линии .

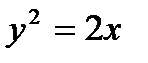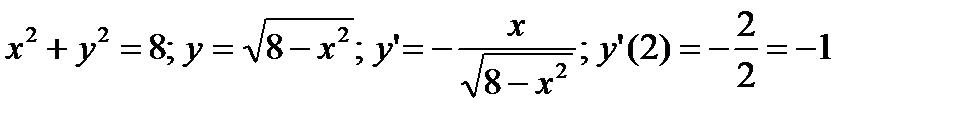- для линии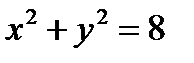

Угол между двумя прямыми определяется формулой: ;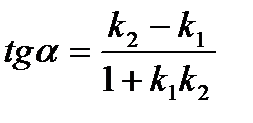

;

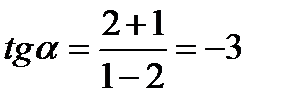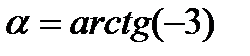
Пример 2.24. Составьте уравнения касательных к линии 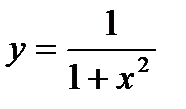в точках ее пересечения с гиперболой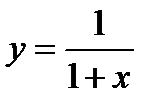

Решение

1) Точки пересечения линий

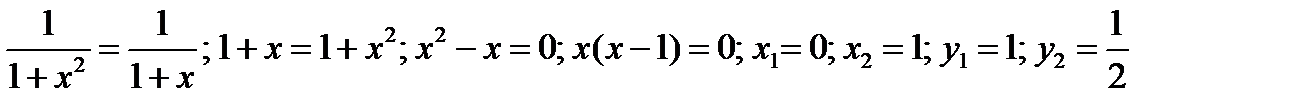
2) Угол наклона к оси x касательной к кривой 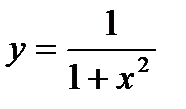в точке :

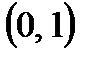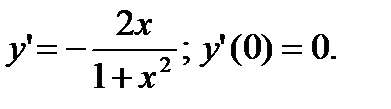
Уравнение касательной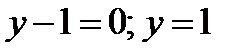

Угол наклона к оси x касательной к кривой 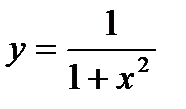в точке :

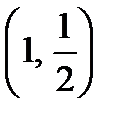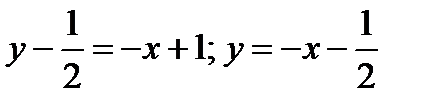
Пример 2.25. Составьте уравнения прямых, проходящих через точку 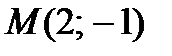и касающихся линии .

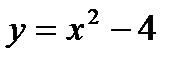Решение. Точка M(2;-1) не является точкой касания, так как .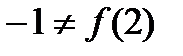

Уравнение касательной, проходящей через точку с абсциссой 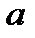, имеет следующий вид: .

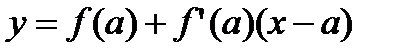Определим значение .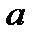

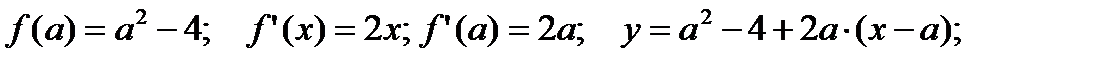
Касательная проходит через точку M (2;-1), следовательно, ее координаты удовлетворяют уравнению касательной.

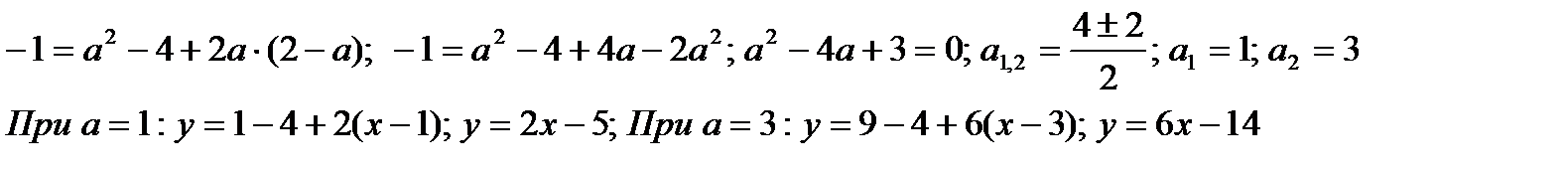
Пример 2.26. Составьте уравнение касательной к линии 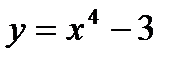, проходящей через точку .

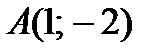Решение. Точка A(2;-1) является точкой касания, так как .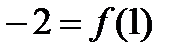

Уравнение касательной имеет следующий вид: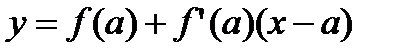

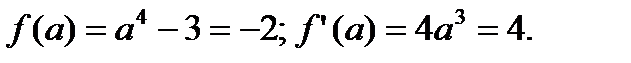
Таким образом, имеем: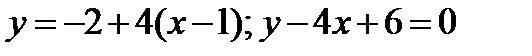

Пример 2.27. Составить уравнение касательной и нормали, прове­денных к кривой 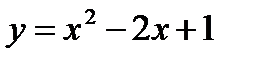в точке, абсцисса которой равна 2.

Решение. Найдем ординату точки касания: 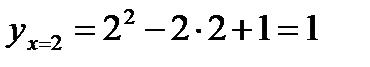. Точка касания 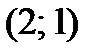. Уравнение касательной 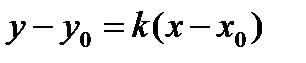;уравнение нормали 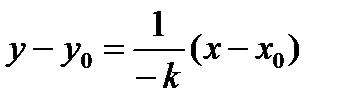, где 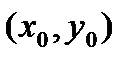- координаты точки касания; k - угловой коэффициент касательной: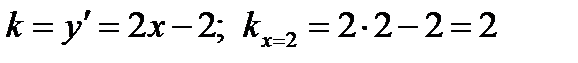

Уравнение искомой касательно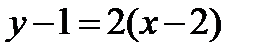й: или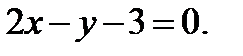

Уравнение норма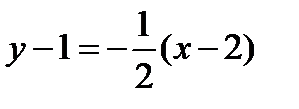ли: или .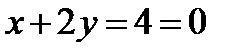

2.6. Механический смысл производной.

Если закон прямолинейного движения точки задан уравнением 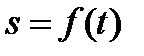, где s - путь; t - время, то мгновенная скорость движения v в момент t определяется равен­ствами

,

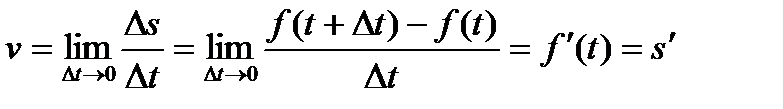т. е. скорость точки при прямолинейном движении в момент време­ни t есть производная от пути s по времени.

Ускорение точки при прямолинейном движении в момент време­ни t есть производная от пути v по времени или вторая производная от пути s по времени.

Пример 2.28. Точка движется прямолинейно по закону 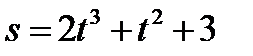. Найти скорость и ускорение в момент ,

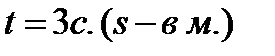Решение.

Находим скорость

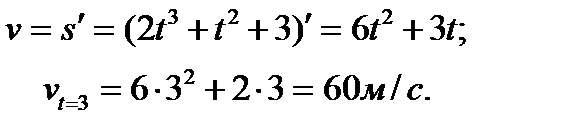
Находим ускорение

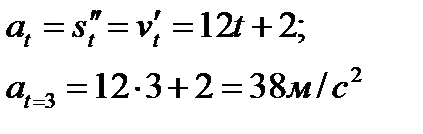
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ