Аналитическая геометрия на плоскости

Если на плоскости заданы две взаимно перпендикулярные оси координат, точкой пересечения которых является точка начала отсчета и определено, какая из осей является первой, а какая второй, то говорят, что в пространстве задана прямоугольная система координат.

Рис.1

Расстояние между точками на плоскости

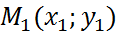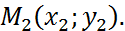Пусть на плоскости заданы точки и Найти расстояние между ними, т.е. найти .

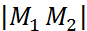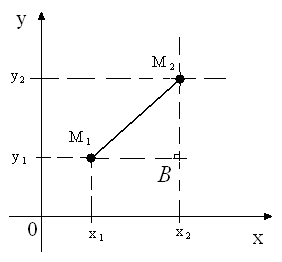
Рис.2

Т.к. треугольник 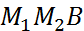прямоугольный, то из теоремы Пифагора следует, что ,

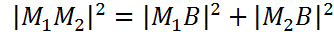а т.к. 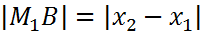и ,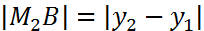

то окончательно получаем, что

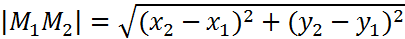. (1)

Координаты середины отрезка с концами в точках и 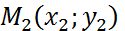определяются по формулам:

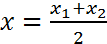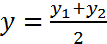и . (2)

Уравнения прямой на плоскости

Простейшей линией на плоскости является прямая. Она может быть задана общим уравнением:

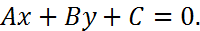(3)

причем постоянные 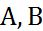не равны нулю одновременно. В зависимости от значений постоянных 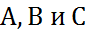возможны следующие частные случаи:

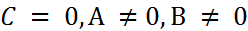- – прямая проходит через начало координат

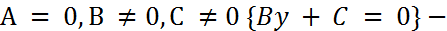- прямая параллельна оси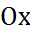

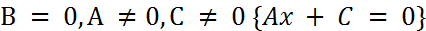- – прямая параллельна оси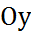

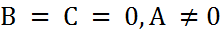- – прямая совпадает с осью

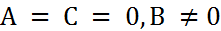- – прямая совпадает с осью

Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

Уравнение прямой с угловым коэффициентом:

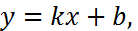(4)

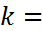где tgα 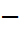угловой коэффициент.

Если прямая проходит через точку 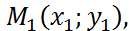то координаты точки удовлетворяют уравнению (4):

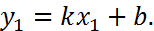
Вычтем из уравнения (4) последнее, получим уравнение прямой, проходящей через заданную точку:

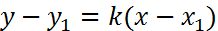. (5)

Также его называют уравнением пучка прямых, т.к. таких прямых множество.

Пусть прямая проходит через две точк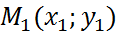и и 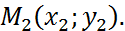Подставим в уравнение (5) координаты точки :

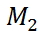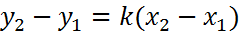и выразим отсюда

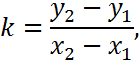
тогда

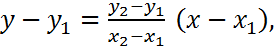
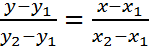. (6)

Получили уравнение прямой через две заданные точки.

Пусть прямая пересекает ось 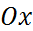в точке 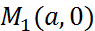а ось 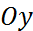— в точке 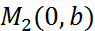. Подставляя в уравнение (6) координаты точек 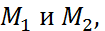выводим уравнение прямой в отрезках:

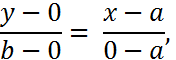
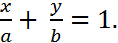(7)

Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых

Пусть даны две прямые 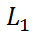и 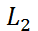заданы уравнениям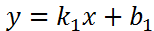и и 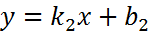(см. рис.3).

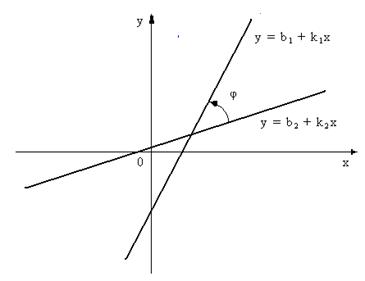
Р и с. 3.

Угол 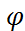между прямыми, на который нужно повернуть прямую 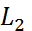против часовой стрелки до совмещения её с прямой 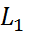найдем по формуле:

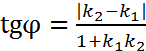. (8)

Условие параллельности прямых: если прямые 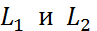параллельны, то 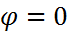и 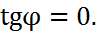Тогда из формулы (8) следует, что 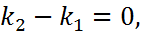т.е.

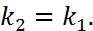(9)

Условие перпендикулярности: если прямые 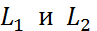перпендикулярны, то 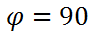и тогда 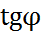не существует, а

t wx:val="Cambria Math"/><w:i/><w:sz w:val="32"/><w:sz-cs w:val="32"/></w:rPr><m:t>1</m:t></m:r></m:sub></m:sSub></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> .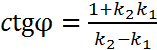

Отсюда

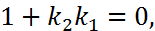
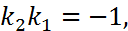
или

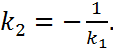(10)

В этом заключается условие перпендикулярности двух прямых.