Производная функции и ее приложения

ВИТЕБСКИЙ ФИЛИАЛ

кафедра математики и физики

ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ

КОНСПЕКТ ЛЕКЦИЙ

по дисциплине

«МАТЕМАТИКА»

для студентов заочной формы обучения уровня ССО

всех специальностей

Витебск2007

Составитель И. А. Шестакова

Рецензент Е.Н. Ермаш

Издание утверждено на заседании кафедры М и Ф

«20» марта 2006 г., протокол № 8

Зав. кафедрой Л.Л. Гладков

Задачи, приводящие к понятию производной

Рассмотрим прямолинейное движение материальной точки и протекание тока в электрической цепи и изучим связанные с ними понятия.

II Протекание тока в электрической цепи

(задача о мгновенной величине тока)

Представим себе электрическую цепь с некоторым источником тока. Обозначим через 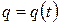количество электричества (в кулонах), протекающего через поперечное сечение проводника за время 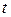. Тогда 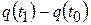есть количество электричества, протекающее через указанное сечение за промежуток времени от момента 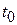до момента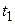

Средней силой тока 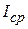за указанный промежуток времени называется число

.

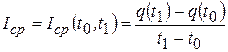В случае постоянного тока средняя сила тока 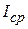будет одинаковой для любых различных, но одинаковых по длительности промежутков времени. Если же в цепи протекает переменный ток, то 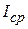будет различной для различных, но одинаковых по длительности промежутков времени.

Поэтому для характеристики цепи переменного тока вводят понятие мгновенной силы тока, или силы тока в данный момент времени:

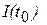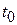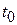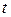Мгновенной силой тока в момент времениназывается предел (если он существует), к которому стремится средняя сила тока за промежуток времени от до при 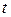, стремящемся к 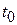, то есть

.

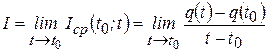Понятие производной функции

В параграфе 1 шла речь о мгновенной скорости движения и о мгновенной силе тока. Введение этих понятий происходило с помощью некоторого предела. Можно привести еще не мало задач, для которых также необходимо находить скорость изменения некоторой функции, например нахождение теплоемкости тела при нагревании, угловой скорости вращающегося тела и др.

I Рассмотрим функцию f(x), xÎ[a;b]

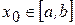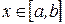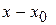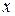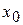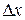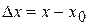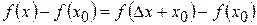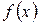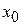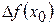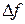Возьмем произвольную точку . Тогда для любого разность называется приращением аргумента в точке и обозначается , то есть . Разность называется приращением функции в точке и обозначается (или , или 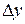), то есть

.

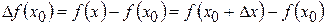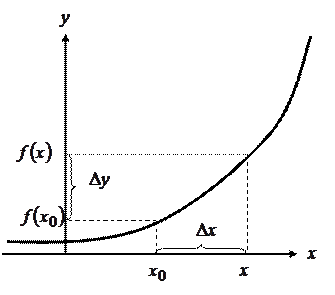
Рис. 2

Производной функции 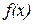в точке 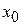называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, если этот предел существует, то есть

.

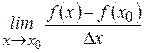Производная функции 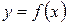в точках 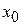обозначается: 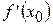или 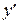(читается: «эф штрих от икс 0» или «игрек штрих»).

Итак, по определению получим, что

.

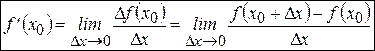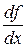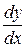Часто для обозначения производной используется символ или (читается «де эф по де икс» или «де игрек по де икс»).

Операция нахождения производной от данной функции называется дифференцированием.

Функция 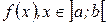, имеющая производную в каждой точке интервала 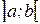, называется дифференцируемой на этом интервале.

II Вычисление производной на основе ее определения

Исходя из определения производной, сформулируем правило нахождения производной функции в точке:

Чтобы вычислить производную функции 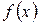в точке 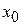нужно:

1. Найти разность ;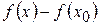

2. Найти отношение ;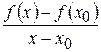

3. Найти предел этого отношения при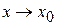

.

Пример 1: Найти производную функции .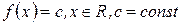

Решение:

1) Находим разность: .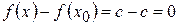

2) Находим отношение: .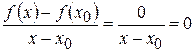

3) Находим предел: .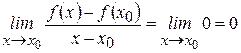

Получили, что .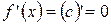

Вывод: Производная постоянной равно нулю.

Пример 2: Найти производную функции .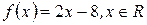

Решение:

1) Находим разность: .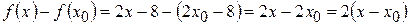

2) Находим отношение: .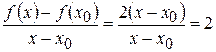

3) Находим предел: .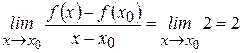

Получили, что .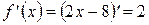

Пример 3: Найти производную функции .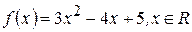

Решение:

1) Находим разность:

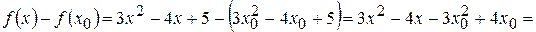
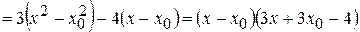
2) Находим отношение:

.

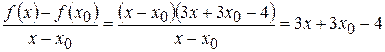3) Находим предел:

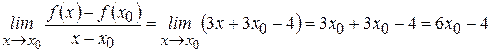
Таким образом 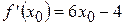. Так как функция 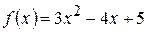имеет производную в любой точке 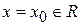, то будем писать .

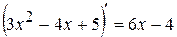Теорема 1

Если функци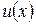и и 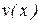имеют производные во всех точках интервала 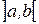, то производная их алгебраической суммы равна алгебраической сумме производных, то есть 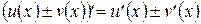для любого .

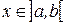Доказательство: рассмотрим функцию 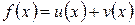, где 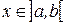и найдем производную этой функции, исходя из определения. Пусть 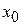– некоторая точка интервала 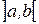. Тогда

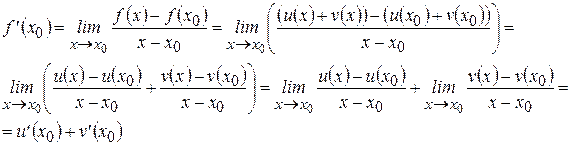
Итак, .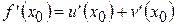

Так как 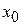– произвольная точка интервала 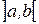, то имеем

.

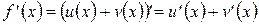Случай разности рассматривается аналогично. Теорема доказана.

Примеры: Найти производную:

1) ;

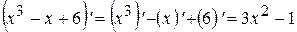2) ;

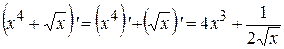Замечание: Данная теорема справедлива для любого числа слагаемых.

Теорема 2

Если функции 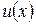и и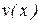меют производные во всех точках интервала 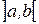, то 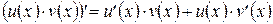для любого .

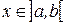Доказательство: рассмотрим функцию 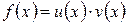, где 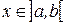и найдем производную этой функции, с помощью определения. Пусть 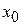– произвольная точка интервала 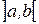. Тогда

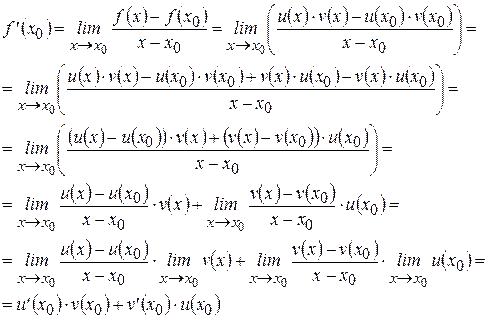
Итак, .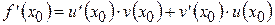

Так как 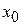– произвольная точка интервала 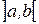, то имеем

.

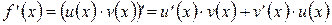Примеры:

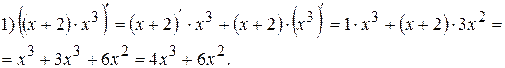
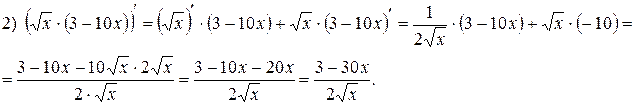
Следствие:Постоянный множитель можно выносить за знак производной:

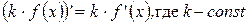
Доказательство:Применим теорему о производной произведения:

.

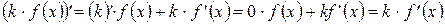Примеры:

;

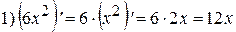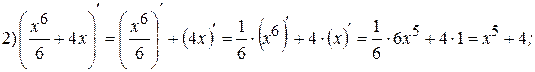
Теорема 3:

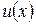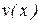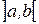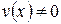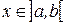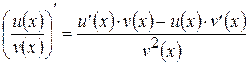Если функции и имеют производные во всех точках интервала , причем для любого , то для любого .

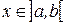Доказательство: Рассмотрим функцию 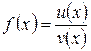, где 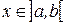и найдем ее производную, пользуясь определением. Пусть 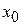– произвольная точка интервала 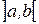. Тогда

.

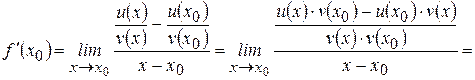
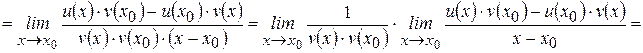
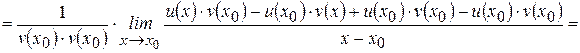
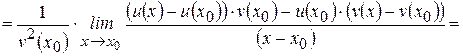
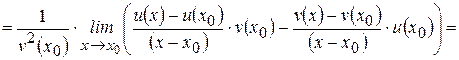
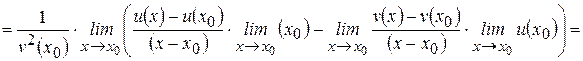
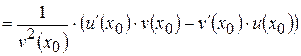Следовательно,

.

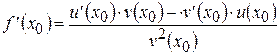А так как 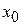– произвольная точка интервала 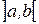, то имеем .

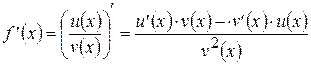Примеры:

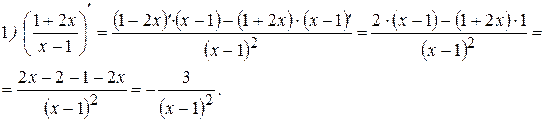
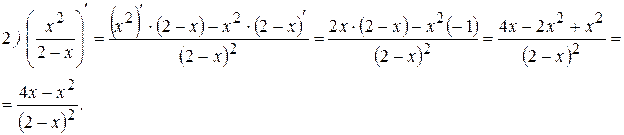
Теорема

Если функция 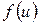дифференцируема по 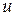, а функция 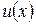дифференцируема по 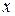, то производная сложной функции 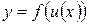по независимой переменной 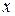определяется равенством: .

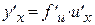Доказательство: Пусть дана дифференцируемая функция 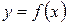, которая является сложной и имеет промежуточный аргумент 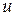зависящий от .

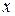По определению производной можем записать 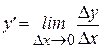. Умножив числитель и знаменатель функции, содержащейся под знаком предела, на приращения промежуточного аргумента 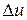, получим:

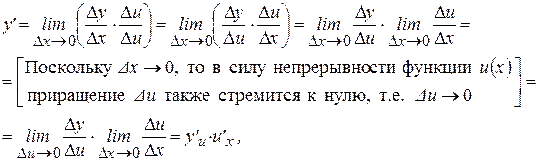
то есть

производная сложной функции 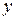по аргументу 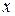равна производной этой функции по промежуточному аргументу 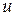, умноженной на производную внутренней функции 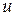по основному аргументу .

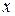Это правило иногда называют правилом цепочки: то есть производная сложной функции равна произведению производных от всех составляющих ее функций. При этом следует помнить, что каждую функцию нужно дифференцировать по ее собственному аргументу.

Пример: Найти производную функции: .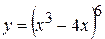

Решение: Эта функция сложная, то есть .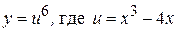

Согласно правилу дифференцирования сложной функции получим: .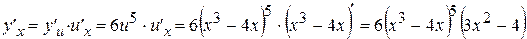

ЛИТЕРАТУРА

1 Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. – М.: Наука, 1980. – Гл. 5. – ÍÍ1-13.

2 Доброхотова М.А., Сафронов А.Н. Функция, ее предел и производная. – М.: Издательство «Просвещение», 1969. – Гл. 6. – ÍÍ51-61, Í65. – Гл. 7. – ÍÍ67-75.

3 Зайцев И.А. Элементы высшей математики. – М.: Наука, 1974.

4 Лисичкин В.Т., Соловейчик И.Л. Математика. Учебное пособие для техникумов. – М.: Высшая школа, 1991. – Гл. 4. – ÍÍ3-7.

5 Яковлев Г.Н. Алгебра и начала анализа, часть I. – М.: Наука, 1987. – Гл. 6, Гл. 7. – ÍÍ34-39.

Содержание

§ 1 Задачи, приводящие к понятию производной………………………………….3

I Прямолинейное движение материальной точки

(задача о мгновенной скорости)………………………………………….……….3

II Протекание тока в электрической цепи

(задача о мгновенной величине тока)……………………………………………5

§ 2 Понятие производной функции………………………………………………….7

§ 3 Производная суммы, разности, произведения и частного функций…………11

§ 4 Сложная функция и ее производная……………………………………………15

§ 5 Производные элементарных функций………………………………………….16

I Производная логарифмической функции……………………………….………..16

II Производная степеннойфункции……………………………………….………...19

III Производная показательной функции………………………………….……….20

IV Производные тригонометрических функций…………………………………..21

V Производные обратных тригонометрических функций……………….……….24

§ 6 Геометрический смысл производной…………………………………………..31

I Определение касательной и нормали к кривой……………………………….…31

II Геометрический смысл производной……………………………………............33

III Уравнение касательной и нормали к кривой………………………….………..35

§ 7 Физический смысл производной…………………………………………….…39

§ 8 Вторая производная и ее физический смысл………………………………….40

§ 9 Дифференциал функции и его геометрический смысл……………………….42

I Геометрический смысл дифференциала………………………………………….43

Литература……………………………………………………………………...45

План 2005/2006, поз.

Шестакова Инга Александровна

ВИТЕБСКИЙ ФИЛИАЛ

кафедра математики и физики

ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ

КОНСПЕКТ ЛЕКЦИЙ

по дисциплине

«МАТЕМАТИКА»

для студентов заочной формы обучения уровня ССО

всех специальностей

Витебск2007

Составитель И. А. Шестакова

Рецензент Е.Н. Ермаш

Издание утверждено на заседании кафедры М и Ф

«20» марта 2006 г., протокол № 8

Зав. кафедрой Л.Л. Гладков